混沌优化算法求解Kepler方程
2012-10-10杨玲玲
杨玲玲, 马 良
(上海理工大学 管理学院,上海 200093)
1 问题的提出
1619年Kepler首次推导出了Kepler方程,该方程在物理、数学领域,特别是在经典天体力学研究中都起着重要作用.
在天体力学和轨道计算中,求解Kepler方程
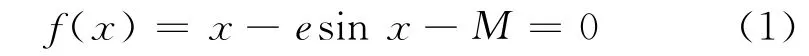
是经常遇到的问题,即在给定平近点角M(0≤M≤π)和偏心率e后去求偏近点角x[1].在椭圆轨道情况下,0≤e≤1.由于方程中含有超越函数sinx,因此,Kepler方程是个超越方程,这意味着x无法用代数方法求出,只能用数值分析或级数求解,这就要求Kepler方程在实际求解中应尽可能地接近真值.
超越方程常用迭代方法求解,目前应用较多的数值迭代方法是不动点迭代法或牛顿迭代法,但前者收敛速度慢,后者在选取初值上要求较高,而且每次都要计算导数值[2].
在实际应用中,由于对上千万年的天体轨道作积分需要反复求解Kepler方程,计算量大且耗时,因此,研究快速求解Kepler方程的方法具有重要的意义[3].本文试图使用一种智能优化算法——混沌优化算法求解Kepler方程,探索从新的角度求解此类问题.
2 现有解法
尽管Kepler方程的提出已近4个世纪,但因其重要性而一直是研究的重要课题.每10~20年就会提出一个新的求解方法.Ng[4]在1979年提出一立方收敛的方法.
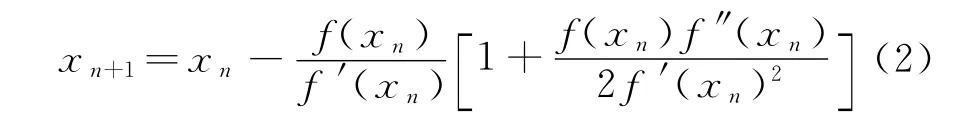
1983年Danby和Burkardt提出了具有立方收敛性的Halley方法.
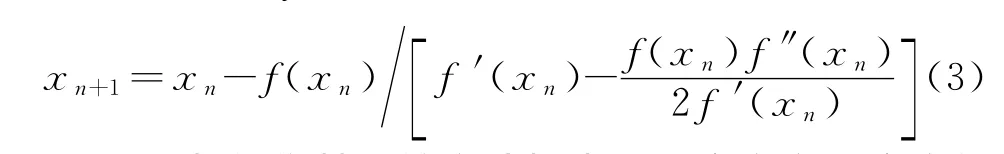
同时,他们基于该方法提出了四次方和五次方的收敛性方法[5].Colwell,Battin和 Vallado分别提出的方法也是以迭代或级数展开为基础的经典方法[6].
3 算法设计
混沌运动具有遍历性、随机性及规律性等特点,它能在一定范围内,按其自身规律不重复地遍历所有状态[7].李兵和蒋慰孙[8]选用Logistic映射做算法
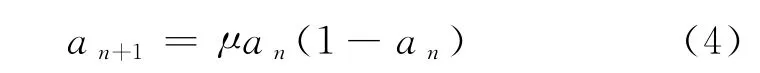
式中,μ为控制参量,取μ=4.
设0≤a0≤1,n=0,1,2,…,当μ=4时,系统完全处于混沌状态,运用载波的方式将混沌状态引入至优化变量中,同时将遍历范围放大到优化变量的取值范围,然后利用混沌变量进行搜索[8].文献[8]中介绍了算法的基本步骤.
针对Kepler方程设计下面的算法.
Step 1 等价转换式(1).
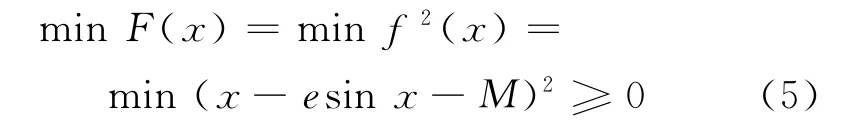
将求解式(1)的问题转化为求x,使得目标函数F(x)=(x-esinx-M)2的值最小.
Step 2 确定x的取值范围.
已知0≤x≤2π,进一步来说,在文献[9]中得出结论

因为f′(x)=1-ecosx≥0恒成立,0≤e≤1,函数f(x)单调递增,同时

故可得出M≤x≤M+e.f(x)的图像如图1所示.

图1 f(x)的图形Fig.1 Graph of f(x)
Step 3 初始化.
设置k=1,a0,最大迭代次数n.
Step 4 根据式(4),产生混沌变量ai.通过式(6),利用载波方式将混沌变量放大到相应优化变量在Step 2中所得到的取值范围.
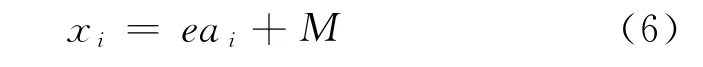
Step 5 如果F(xi)<F*,那么F*=F(xi),x*=xi;否则,放弃xi.
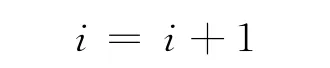
Step 6 如经若干次搜索后保持不变,则按式(7)进行第二次载波.
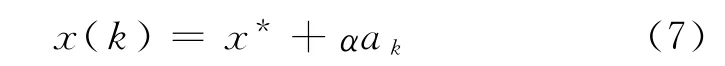
式中,x*为当前最优解;α为较小的调节常数,本文中取小于1的常数.
Step 7 如果F[x(k)]<F*,那么F*=F[x(k)],x*=x(k);否则,放弃x(k).

Step 8 当达到最大迭代次数时,终止搜索,输出最优解x*,F*.
不难估算,该算法的时间复杂度为O(n),n为最大迭代次数.
4 数值测试
为检验求解效果,进行了一系列数值测试计算,并与已有方法进行比较.实验所用的硬件为Pentium(R)4CPU 2.80GHz,256MB内存的微机,软件为 Windows XP操作系统和Matlab7.0运行环境.
在现有文献中,大多数计算实例是在M=0和e=1附近进行的,因为,在这一点有f′=f″=0,在运用传统方法时容易导致解法不收敛,本文首先求解了这类情况,现列出部分结果.表1和表2分别列出了迭代次数为1 000和10 000时,在临界情况(零平近点角和等于1的偏心率,即M=0,e=1)附近的测试结果,混沌初值a0=0.201 7.
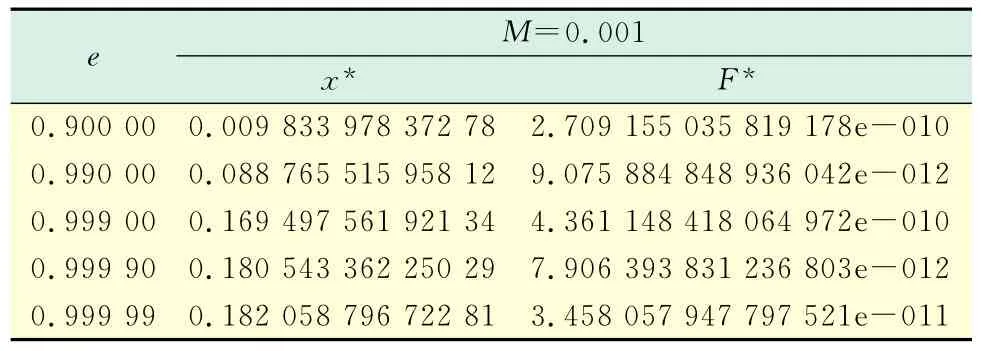
表1 最大迭代次数为1 000时的结果Tab.1 Results of n=1000
从表1和表2中可以看出,迭代次数越大,求解精度越好.由于算法的时间复杂度较低,算法的运行时间基本可以忽略不计.
文献[10]中指出,用改进的牛顿法求解时可能收敛至一个或多个错误的值,例如,当M=1.347,e=0.66,迭 代 序 列 在 0.448 902,0.354 721,0.469 946和0.362 751这4个值上循环,而此时的正确解是1.958 11[10].所以,本文也对该情况进行了求解,求解结果为

表2 最大迭代次数为10 000时的结果Tab.2 Results of n=10 000

本文还测试了文献[3]和文献[10]中的一些算例,结果如表3所示.
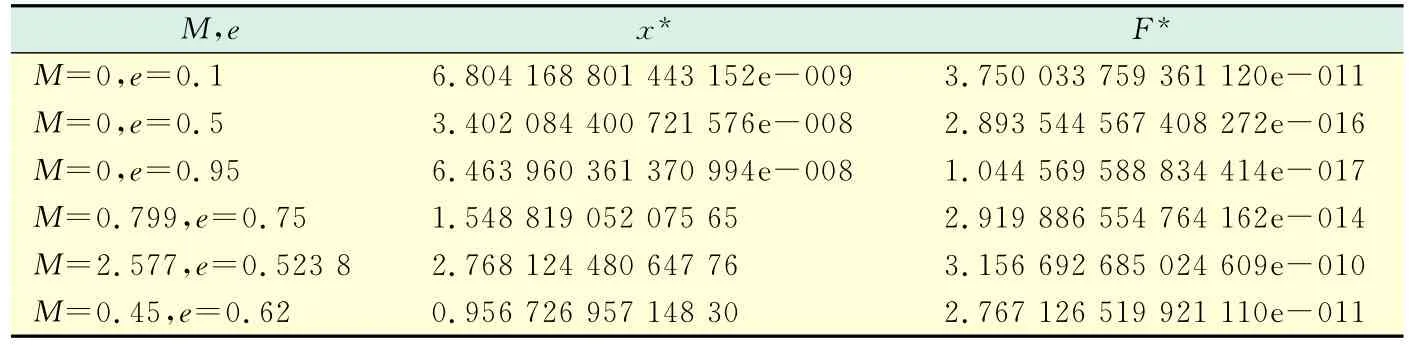
表3 部分算例测试结果Tab.3 Part of test results
测试结果表明,混沌优化算法对于Kepler方程求解的有效性,该算法较低的时间复杂度提升了运算的效率,且免除了多次求导的复杂运算,避免了在临界状态容易不收敛的缺点.
5 结 论
常见的求解Kepler方程的方法是简单迭代法、牛顿法等经典方法,本文运用智能优化方法——混沌优化算法求解该问题.算法的时间复杂度较低,具有较高的运算效率,同时避免了传统方法中多次求导等复杂计算,且取得了满意的结果.对于Kepler方程,本文所给出的混沌优化算法是一种简单而又快速地获得有效解的途径.
[1]周庆林,黄天衣.Kepler方程的解法[J].天文学报,1988,29(1):106-112.
[2]束雄英,李红.Kepler方程的一种迭代加速[J].航空计算技术,2005,35(1):41-44.
[3]王玉诏,钟双英,孙威,等.Kepler方程的六阶迭代解法[J].江西科学,2009,27(6):790-792.
[4]Colwell P.Solving Kepler’s equation over three centuries[M].Richmond:Willmann-Bell,1993.
[5]Danby J M A,Burkardt T M.The solution of Kepler’s equation[J].Celestial Mechanics,1983,31(2):317-328.
[6]Davis J J.Sequential solution to Kepler’equation[J].Celest Mech Dyn Astr,2010,108(7):59-72.
[7]苗东升.系统科学大学讲稿[M].北京:中国人民大学出版社,2007.
[8]李兵,蒋慰孙.混沌优化方法及其应用[J].控制理论与应用,1997,14(4):613-615.
[9]Smith G R.A simple,efficient starting value for the iterative solution of Kepler’s equation[J].Celestial Mechanics,1979,19(2):163-166.
[10]岳锦海,黄天衣.椭圆Kepler方程求解中的非线性现象[J].南京大学学报(自然科学版),1998,34(1):21-28.
