基于声发射技术的液固体系颗粒粒径测量

黄春燕， 蔡小舒， 周 骛

（上海理工大学 能源与动力工程学院，上海 200093）

随着测量技术的不断发展，对液固体系中固体颗粒状态的监控测量要求越来越高.常用的近红外光谱NIR［1］（near－infrared spectroscopy）和拉曼光谱法（Raman spectroscopy）［2］在测量中需要开设特定的测量窗口才可以使用，不利于测量装置安装.而声发射技术作为一种有效的非侵入式检测方法，其传感器并不直接和测试对象接触，可免于被腐蚀或污染，且可以很便捷地安装在容器和管道外壁上，便于维护.

Boyd［3］对声发射技术在化工领域的应用情况进行了综述，其中大多数研究侧重于声发射信号定性的规律性研究［4－5］.Nordon对液固反应器影响声发射测量的因素进行了研究［6］；国内阳永荣等利用声发射技术对搅拌釜中液位、搅拌速度、浓度等进行了测量研究［7－8］.但直接从声发射机理出发实现液固体系固体颗粒参数测量的研究还不多见，因此有必要对声发射颗粒测量技术进行专门的研究.

文中搭建了一套液固体系声发射信号测量装置，采用宽带声发射传感器和高速数据采集卡采集水－玻璃微珠液固体系的声发射信号，主要研究颗粒浓度、颗粒粒径等对声发射信号特征的影响，并基于频谱特征分析，结合基于Hertz－Zener理论的频谱估算式，实现玻璃微珠粒径的测量.

1 理论频谱估算

工业场合常见的声发射信号主要是由颗粒与管道、容器壁面碰撞产生，其声发射机理可简化为颗粒和平板的碰撞.当平板在单位面积上受到碰撞力F（r，θ，t）的作用会产生位移u（r，θ，t），其运动方程用极坐标表示为

式中，ρ为平板密度；h为平板厚度；E为平板杨氏弹性模量；ν为平板泊松比.

Akay［9］结合 Hertz－Zener理论［10］推导得出了平板受到球形颗粒碰撞后所产生的振动的位移时域表达式，它由两部分组成，当0＜t≤π／ω0时为受迫振动；当t＞π／ω0时为自由振动，ω0为振动基频，与碰撞时间有关.

Carson［11］在此基础上进一步研究了位移加速度频谱的变化情况，并发现忽略位移u（r，t）的表达式中的受迫振动部分并不会对整个位移加速度频谱波形产生显著影响，由此推导得到的平板振动位移加速度频谱估算近似表达式为

其中

式中，F0为颗粒碰撞平板的最大碰撞力；m为平板质量；ωn为平板振动频率.

2 液固实验装置

图1为实验装置示意图.实验在容量为2L的玻璃烧杯中进行，宽带声发射传感器的频响范围为50～750kHz，经甘油耦合固定在烧杯外壁面.液相分散介质为水，固相介质为由浙江天台精工西力玻璃微珠有限公司提供的GT－Ⅱ型玻璃微珠，粒径范围分别为1＃：200～400μm，2＃：400～600μm，3＃：600～800μm，密度为2 230 kg／m3，泊松比为0.2，杨氏模量为6.4×109N／m2.实验中在烧杯外壁面6个不同位置（200，400，600，800，1 000，1 200 mL刻度位置）测量声发射信号，经前置放大器放大后由高速采集卡采集送入计算机，采样频率设为40 MHz.整个测量过程中，搅拌速度设为850 r／min，以保证所有粒径的玻璃微珠相对均匀地分散于水中.多次连续采集的数据存入一个数据文件，同一条件进行多次采集以备分析处理.采用MATLAB软件编制程序实现数据处理.

图1 液固实验装置示意图Fig.1 Schematic of liquid－solid experiment

3 玻璃微珠质量浓度对信号功率谱估计的影响

首先对信号进行零均值处理，目的是为了消除数据中的直流分量，且若不去除均值，可能会导致在低频段的功率谱估计产生较大误差.功率谱估计采用Welch算法［12］，又称加权交叠平均法，该方法是对经典谱估计周期图法的改进，其基本思想是利用分段加窗的方法把一长度为N的数据xN（n）分成L段，每段长度为M＝N／L，允许每段数据有部分重叠，且各段数据互为独立.将每段的功率谱加以平均得到平均功率谱.与标准离散傅里叶变换相比，该方法在控制估计方差和频谱泄漏方面有明显改善.计算时将数据等分为100段，重叠率取50%，选用Blackman窗函数.

考虑到在搅拌情况下，玻璃微珠在轴向位置会存在分布的不均匀性.为减少由此造成的数据处理误差，在同一玻璃微珠粒径和质量浓度下，每个测量点取10组数据作功率谱估计，这6个测量点的平均值看作为该条件下的功率谱估计值.由此推算出的粒径可看作是玻璃微珠颗粒系的平均粒径.图2、图3分别给出了为1＃和3＃玻璃微珠在不同质量浓度ρS下的功率谱估计B和频率f的关系.

图2 1＃玻璃微珠不同质量浓度下的功率谱估计Fig.2 Power spectrum estimation under different concentration of 1＃ glass bead

图3 3＃玻璃微珠不同质量浓度下的功率谱估计Fig.3 Power spectrum estimation under different concentration of 3＃ glass bead

从整体规律上看，随着质量浓度的增加，在大部分频段上功率谱估计幅值均表现出增加的趋势.为了更直观地考察玻璃微珠质量浓度对功率谱估计的影响，并根据实测信号功率谱估计的频率分布范围，求取0～700kHz频率范围内的功率谱估计的面积，用S表示.图4给出了3种玻璃微珠的质量浓度和功率谱估计面积S关系，可以看到，3种玻璃微珠的质量浓度均和功率谱估计面积呈良好的线性关系.显然，随着玻璃微珠质量浓度增加，玻璃微珠碰撞烧杯壁面的几率和次数也增多，从而造成功率谱估计幅值强度增大.同时还发现在质量浓度相同的情况下，虽然粒径大的个数比小颗粒的个数少，但是功率谱估计的面积值对粒径大的颗粒的质量浓度改变更为敏感.由此可以看出，就粒径和质量浓度相较而言，粒径大小对功率谱估计的影响更大.图4的结果表明可利用功率谱估计面积这一参数和颗粒质量浓度的关系来监控工业上的液固体系的颗粒质量浓度的变化情况.

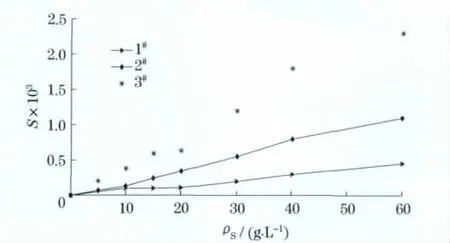
图4 玻璃微珠质量浓度和功率谱面积的关系Fig.4 Relationship of concentration of glass bead with area of power spectrum estimation

4 玻璃微珠粒径估算

4.1 碰撞速度的计算

采用计算流体力学软件FLUENT模拟计算颗粒碰撞壁面的速度.利用离散颗粒模型模拟玻璃微珠在搅拌过程中的运动情况，以获取玻璃微珠碰撞壁面的速度.模拟过程采用非稳态数值求解，对湍流的处理采用Realizablek－ε模型，边界层采用标准壁面函数进行处理.材料参数、模拟条件等设置与实验相同.初始时刻，容器上部为空气，气液速度为零；桨叶设置为移动壁面边界，在桨叶的带动下气液旋转速度逐渐增加，待气液两相流动稳定后加入颗粒相，在颗粒相流动稳定后提取壁面附近颗粒的速度值.

4.2 玻璃微珠粒径估算

将3种玻璃微珠平均粒径（283，490，693μm）作为输入粒径，并将模拟计算出来的碰撞速度代入频谱估算式，计算出3种粒径玻璃微珠的理论频谱B′，结果如图5所示.比较图2、图3和图5发现，对于1＃玻璃微珠，实测功率谱估计的主频位于260 kHz左右，理论频率估计中主频位于230 kHz，而3＃玻璃微珠的实测主频转移到低频约40 kHz的位置，理论频率估计中主频位于60 kHz，这表明理论和实测信号的频谱主频较为接近，且随着颗粒粒径的变化，理论和实测频谱表现出较为一致的频谱能量迁移规律，即随着颗粒粒径增大，声发射信号能量逐渐向低频分布.因此利用这一特点，对其频谱值在0～700 kHz频段区间作归一化处理，对频谱的归一化处理既消除了信号强弱的差异性，又保留了信号随粒径变化规律性的成分.图6给出了玻璃微珠不同粒径、质量浓度下的功率谱估计归一化，可以看出，当玻璃微珠质量浓度在20 g／L时，3种粒径下的功率谱估计归一化情况对质量浓度不敏感，也即在后续的粒径估算中，将选择各个粒径下质量浓度在20 g／L以上的数据.

图5 3种玻璃微珠的理论频谱估计Fig.5 Theoretical frequency spectrum of three kinds of glass bead

通过寻找出最接近实测信号的理论估算频谱，就有可能估算出颗粒粒径，此处考虑用最小二乘法对实测功率谱估计和给定粒径D的理论频谱估算进行拟合，两者最小化误差的平方和用g（D）表示，计算公式如下：

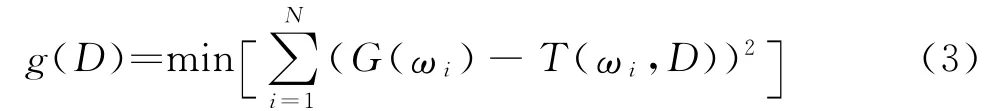
式中，G（ωi）为实测信号功率谱估计的归一化值；T（ωi，D）为给定粒径时得到的理论功率谱估计归一化值.若D取到某一数值时，使得g（D）达到最小，则此时D值即看作是实测颗粒粒径的估算值.

图6 不同粒径、质量浓度下的功率谱估计归一化Fig.6 Scaled power spectrum estimation under different particle size and concentration

图7给出了1＃玻璃微珠的实测信号功率谱归一化值和给定粒径的理论估计频谱归一化值，求取不同给定粒径下的f（D）值时颗粒粒径间隔10μm取值，结果表明，当粒径设为210μm时g（D）值取最小值，因此将210μm作为实测颗粒的粒径估算值.根据相同的方法，得到其它2种玻璃微珠的粒径估算值，结果如表1所示.

表1 玻璃微珠粒径理论估算值Tab.1 Estimated particle size of glass bead

图7 1＃玻璃微珠实测信号和理论频谱的归一化值Fig.7 Comparison of theoretical and experimental scaled power spectrum estimation（1＃ glass bead）

结果表明，利用式（2）的理论频谱估算式并结合式（3）的数据处理方法可实现玻璃微珠粒径的估算，估算结果较好地区分了3种不同粒径的玻璃微珠，说明了该颗粒粒径测量方法的可行性和有效性.

5 结 论

a.利用宽带声发射传感器和高速数据采集卡采集的声发射信号经Welch算法求取功率谱估计，玻璃微珠的质量浓度和功率谱估计面积有良好的线性关系.和质量浓度相较，颗粒粒径对功率谱估计的影响更大.结果表明，可利用功率谱估计面积这一参数和颗粒质量浓度的关系来监控液固体系的颗粒浓度变化情况.

b.采用计算流体力学软件FLUENT模拟计算得到颗粒碰撞壁面的速度，通过对理论频谱和实测信号功率谱估计的分析比较，采用最小二乘方法估算出玻璃微珠的粒径，其结果和实际平均粒径较为接近，粒径范围较为吻合，表明该理论计算式和数据处理方法用于实现颗粒粒径测量的可行性和有效性.

［1］El－Hagrasy A S，Morris H R，D’Amico F，et al.Nearinfrared spectroscopy and imaging for the monitoring of powder blend homogeneity［J］.J Pharm Sci，2001，90（9）：1298－1307.

［2］Clegg I M，Everall N J，King B，et al.On－line analysis using Raman spectroscopy for process control during the manufacturing of titanium dioxide［J］.Appl Spectrosc，2001，55（9）：1138－1150.

［3］Boyd J W R，Varley J，The uses of passive measurement of acoustic emissions from chemical engineering processes［J］.Chemical Engineering Science，2001，56（5）：1749－1767.

［4］Hou R，Hunt A，Williams R A.Acoustic monitoring of hydrocyclones［J］.Powder Technology，2002，124（3）：176－187.

［5］Huang J，Ose S，Silva S，et al.Non－invasive monitoring of powder breakage during pneumatic transportation using acoustic chemometrics ［J］.Powder Technology，2003，129（1），130－138.

［6］Nordon A，Carella Y，Gachagan A，Littlejohn D，et al.Factors affecting broadband acoustic emission measurements of a heterogeneous reaction［J］.Analyst，2006，131（2）：323－330.

［7］曹翌佳，王靖岱，阳永荣.声波信号多尺度分解与固体颗粒质量流率的测定［J］.化工学报，2007，58（6）：1404－1410.

［8］张晓欢，声发射信号的多尺度分析及在固－液体系中的应用［D］.杭州：浙江大学，2002.

［9］Akay A，Tokunaga M，Latcha M.A theoretical analysis of transient sound radiation from a clamped circular plate［J］.J App Mech，1984，51（1）：41－47.

［10］Zener C.The intrinsic inelasticity of large plates［J］.Phys Rev，1941，59（8）：669－673.

［11］Carson G.Particle sizing using Hertz－Zener theory and ultrasonic measurement of impact vibrations［D］.Glasgow：University of Strathclyde，2008.

［12］杨晓明，晋玉剑，李永红.经典功率谱估计Welch法的MATLAB仿 真 分 析 ［J］.电 子 测 试，2011，7：101－104.