追捕逃逸型微分对策问题的识别域判别

张 霞， 高 岩， 夏尊铨

（1.大连理工大学 数学科学学院，大连 116024；2.浙江财经学院东方学院 信息分院，海宁 314408；3.上海理工大学 管理学院，上海 200093）

1 问题的提出

微分对策理论是现代控制理论中的一个重要研究课题，也是对策论的一个重要分支.微分对策是指在局中人之间进行对策活动时要用到微分方程（组）来描述对策现象或规律的一种对策，是解决对抗与竞争问题的有力工具.微分对策理论的研究可追溯到20世纪40年代，当时因军事上的需要，由Isaacs带领的团队研究了导弹对抗飞行器策略问题，以此为开端，微分对策的基本概念及理论相继提出，最早的文献见于Isaacs的《Differential Games》一书［1］.微分对策理论的进一步发展来自两个方面：一是最优控制理论；二是对策论.从最优控制到微分对策可看作是从一方控制发展到双方或多方控制；从对策论到微分对策，又可看作是从静态的对策理论发展到动态的对策理论.因此，微分对策理论的研究对控制领域和对策论中问题的解决起着重要的作用［2］.而且随着该理论的不断发展，现在也被广泛应用到科学研究、工程技术、交通运输、航天航空、环境保护、经济管理和市场竞争等许多方面［3－5］.

根据提法的不同，微分对策问题有多种形式.本文将考虑单目标两人追捕逃逸型微分对策问题（pursuit－evasion games），它是由Isaacs最早提出并命名的.描述如下：

考虑两控制变量的微分动力系统

其中，x∈Rn是状态变量；u∈U，v∈V是控制变量；U，V⊂Rm，f（x，u，v）为Rm＋n到Rm上的利普希茨函数.设Ω为Rn中开子集，也称为目标.引入两个局中人，第一个局中人为Ursula，控制变量为u，要使系统的状态在有限时间内到达目标Ω；另一个局中人为Victor，控制变量为v，却力争使系统状态永远避开此目标Ω，这就是单目标两人追捕逃逸型微分对策问题.

Krasovskii及Subbotin研究了追捕逃逸型微分对策问题的无优先规则的位置策略［2，6］，并证明了选择定理.即在任何初始点x0，或者Ursula赢，或者Victor赢，二者择一.然而，在Caratheodory意义下系统（1）无解，为此他们推广了解的定义，给出了近似微分对策.与位置策略的研究方法不同，文献［7］使用了无预见性策略（nonanticipative stragies），故局中人都可以通过对方行动的信息来决定自己的行动，这在现实中有很多应用事例.文献［7］的另一个重要贡献在于通过几何方式去研究胜利域（victory domain，指无论对方如何行动，局中人都能赢的初始点的集合），据此可以继续作胜利域的数值计算［8－9］.随后又在文献［10］中给出了具有状态约束的追捕逃逸型问题，并证明了微分对策值的存在性.近期作者又将这一理论推广到混杂系统［11］.

就具体应用问题来讲，微分对策系统识别域（discriminating domain）的判别很重要，它直接关系到胜利域的表示以及微分对策问题的解.然而，正如对一般的非线性控制系统可生存性判别的充要条件很难具体使用一样［12］，目前关于微分对策问题的识别域判别还没有切实可行的判别准则.为此，本文参照文献［13］的方法，研究了一类重要的控制系统即仿射非线性控制系统下的追捕逃逸型微分对策问题，给出该问题的系统识别域判别的方法，并结合凸可行问题的算法给出该判别问题的投影算法，最后给出这类微分对策问题的选择定理.

2 识别域的判别方法

首先给出文中用到的几个定义.

定义1K为Rn的闭子集，x∈K，若dK（x＋p）＝‖p‖，则称向量p∈Rn为K在x处的近似法向量，所有p的集合记为NPK（x）.

定义2 若任意x∈D，任意p∈NPD（x），则称D为f的识别域.Rn的闭子集K所包含的f的最大识别域称为f的识别核，记作Discf（K）.

定义3 若任意x∈D，任意p∈NPD（x），则称D为f的领导域（leadership domain）.Rn的闭子集K所包含的f的最大的领导域称为f的领导核，记作Leadf（K）.

下面讨论识别域的判别问题.考虑如下仿射非线性系统

其中，w（x）为Rn到Rn的利普希茨函数，g（x）和h（x）为Rn到Rm＋n的利普希茨函数，u∈U为一度量紧空间.v∈V＝｛v∈Rm｜ai（v）≤0，i＝1，2，…，r｝，ai（v）为Rm上的凸函数.

定义区域

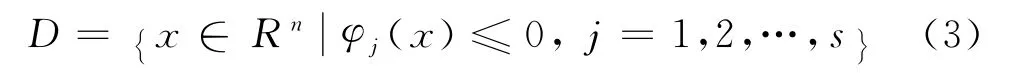
这里给定φj（x）为Rn上的连续可微函数.定义指标集

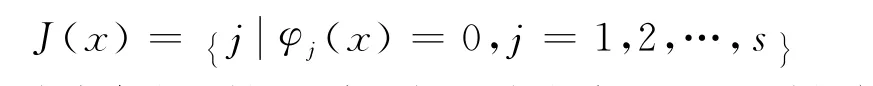
为方便问题的研究，在此给出本文所用到的假设条件及已知命题.

假设1

a.f（x，u，v）｜Rn×U×V→Rn为连续函数.

b.对任意u∈U，v∈V，f（·，u，v）为利普希茨连续.

假设2［14］存在y0∈Rn，使得φj（x）Ty0＜0，j＝1，2，…，s.

假设3［14］cl（γ（x））＝Γ（x）成立，其中

这里cl为闭包.

命题1［14］若假设2及假设3成立，则TD（x）＝Γ（x）.其中

命题2［15］若假设1成立，则D为f的识别域的充要条件是：

任意x∈D，任意u∈U，f（x，u，V）∩TD（x）≠φ其中为空集.

下面给出判别系统（2）的识别域的充分必要条件.

定理1 在假设1～3成立的条件下，区域D为系统（2）中f的识别域当且仅当不等式组

是相容的.其中，v∈Rm为变量.

证明 由命题1知，区域D为f的识别域的充要条件是：

任意x∈D，任意u∈U，f（x，u，V）∩TD（x）≠φ.当x属于区域D的内部时，TD（x）＝Rn，定理显然成立.因此只需考虑边界点的情况，即集合.此时由命题1知，

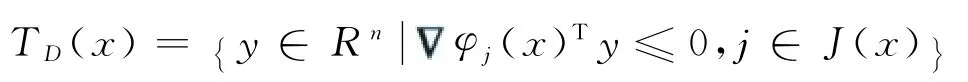
所以f（x，u，V）∩TD（x）≠φ等价于下面的不等式组有解

将y＝w（x）＋g（x）u＋h（x）v代入上面的第二个不等式，即得式（4a）和式（4b），证毕.

3 投影算法及选择定理

下面给出判别系统（2）的识别域的算法.

因为式（4a）是关于变量v的线性不等式组，故可与式（4b）一起组成下面的凸不等式组

其中，v∈Rm为变量，q为式（4a）和式（4b）中全部不等式的个数.

判别该凸不等式组的相容性又可视为凸可行问题，令

则问题转化为寻找v∈Ψ.解决此问题的一个强有力的方法是投影算法［16］，下面给出判别识别域的投影算法.

Step 2i＝0，0＜η≤1，取v0∈Rm.

Step3 若点列｛vi｝收敛，则停止，x∈D为f的识别域中的点.否则转至Step 4.

Step 4 计算σk∈∂ak（vi）＝｛σk∈Rn｜z∈Rn，ak（z）≥ak（vi）＋［vi，z－vi］｝，

Θi＝｛y∈Rn｜ak（vi）＋〈σk，y－vi〉≤0，k＝1，2，

Step 5 选择ωi｜η≤ωi≤2－η，计算vi＋1＝vi＋ωi（yi－vi）.

Step 6i＝i＋1，转至Step 3.

定理2（收敛性） 在下列条件成立的情况下，算法收敛，即｛vi｝→v∈Ψ.

a.ai（v）≤0，i＝1，2，…，r为凸连续函数；

b.Ψ≠φ；

c.对任意v，∂ai（v）是有界的，i＝1，2，…，r.

最后回到两人追捕逃逸型微分对策问题，给出在仿射非线性系统下的选择定理.

定理3 设f满足假设1，令Ο＝Rn＼Ω，则Victor的胜利域为Discf（Ο），Ursula的胜利域为Ο＼Discf（Ο）.

证明 参照文献［7］的选择定理可以得到Victor的胜利域为Discf（Ο），Ursula的胜利域为Ο＼Leadf（Ο）.又因为f（x，u，v）＝w（x）＋g（x）u＋h（x）v，故

即Isaacs条件满足，所以Leadf（Ο）＝Discf（Ο），故结论成立，证毕.

由此可见，在这种特殊情况下，局中两人的胜利域瓜分了目标集的补集.而且该微分对策问题与无优先规则的位置策略相同，故只要知道系统的初始状态，就能确定两人的对策结局.

4 结 论

本文基于非光滑分析及生存理论得出了一类仿射非线性微分对策问题在不等式约束区域上系统识别域的判别方法，该方法可具体实现；并给出了算法，以及两人追捕逃逸型微分对策问题的选择定理.虽然微分对策理论的研究及应用有了极大的发展，但在追捕逃逸型微分对策模型的建立和求解以及不确定型微分对策等方面的研究尚不充分，这可作为进一步研究的课题.

［1］Isaacs R.Differential games［M］.New York：Wiley，1965.

［2］Krasovskii N N，Subbotin A I.Game theoretical control problems ［M ］. New York： Spring－Verlag，1988.

［3］Getz W M，Pachter M.Two－target pursuit－evasion differential games in the plane［J］.JOTA，1981，34 （3）：383－403.

［4］Zhu Q Y，Tembine H，Basar T.Hybrid risk－sensitive mean－field stochastic differential games with application to molecular biology［C］／／2011 50th IEEE Conference on Digital Object Identifier.Orlando，2011：4491－4497.

［5］Steffen J，Georges Z.Developments in differential game theory and numerical methods：economic and management applications［J］.Computational Management Science，2007，4（2）：159－181.

［6］Krasovskii N N，Subbotin A I.Universal optimal strategies in positional differential games ［J］.Differential Equat，1984，19（11）：1377－1382.

［7］Cardallaguet P.Differential game with two players and one target［J］.SIAM J Control and Optimization，1996，34（4）：1441－1460.

［8］Quincampoix M，Saint－pierre P.An algorithm for viability kernels in Holderian case：approximation by discrete viability kernels［J］.Journal of Math System，Estim and Control，1995，5（1）：115－118.

［9］Cardallaguet P，Quincampoix M，Saint－pierre P.Some algorithms for differential games with two－players and one target［J］.Mathematical Modeling and Numerical Analysis，1994，28（4）：441－461.

［10］Cardallaguet P，Quincampoix M，Saint－pierre P.Pursuit differential games with state constraints［J］.SIAM J Control and Optimization，2002，39（5）：1615－1632.

［11］Gao Y，Lygeros J， Quincampoix M. On the reachability problem for uncertain hybrid systems［J］.IEEE Transactions on Automatic Control，2007，52（9）：1572－1586.

［12］高岩.一类非线性控制系统可生存性判别［J］.信息与控制，2005，34（4）：510－512.

［13］高岩.仿射非线性控制系统生存性的判别［J］.控制理论与应用，2009，26（6）：654－656.

［14］Demyanov V F， Rubinov A M. Constructive nonsmooth analysis［M］.Berne：Peterlang，1995.

［15］Aubin J P.Viability theory［M］.Boston：Birkhäuser，1992.

［16］Garcia－palomares U M.A superlinearly convergence projection algorithm for solving the convex inequality problem［J］.Operations Research Letter，1998，22（2／3）：97－103.