关于丢番图方程x(x+1)(x+2)=2pyn

管训贵

(泰州师范高等专科学校数理信息学院，江苏泰州225300)

1 引言及主要结论

1875年，数学家 Lucas［1］问:方程:

是否仅有正整数解(x，y)=(1，1)，(24，70).这一问题，直到1971 年，才由 Ljunggren［2］利用四次域理论给出了肯定的回答.1981年，Watson［3］利用椭圆函数的性质给出了全新的证明.1985年，马德刚［4］又给出了一个期待已久的初等证明.然而问题并未因此而结束.注意到方程(1)能改写成2x(2x+1)(2x+2)=6(2y)2，因而可得方程:

在2∣x 时的全部正整数解为(x，y)=(2，2)，(48，140).1996 年，曹珍富［5］证明了方程:

本文对更一般的方程:

的解进行了研究，得到以下结论.

定理1 若p是奇素数，n是大于2的整数，则方程(4)仅有正整数解(p，x，y)=(3，1，1).

定理2 若 p 是奇素数，n=2，则方程(4)在 p≢1(mod 8)时仅有正整数解(p，x，y)=(3，1，1)，(3，2，2)，(3，48，140)，(11，98，210);在 p≡1(mod 8)时的正整数解为(p，xn，yn)=(p，16t2n，4untnsn)，这里 p，un，tn，sn满足 sn+2=6sn+1－sn，s1=3，s2=17，tn+2=6tn+1－tn，t1=1，t2=6 及 pu2n=16t2n+1.

推论1 若 p是奇素数，n=2，则方程(4)在 p≡1(mod 8)，x＜2.58×1059时仅有正整数解(p，x，y)=(17，16，12)，(577，576，408)，(665857，665856，470862).

2 若干引理

引理1 设n是大于1的整数，则方程X2－1=Yn仅有正整数解(X，Y，n)=(3，2，3).

证明 可参见文献［6］.

引理2 方程X2－2Y4=1没有正整数解(X，Y).

证明 可参见文献［7］.

引理3 设q是奇素数，m是正整数，则方程:

的整数解(X，Y，Z，m)满足 m≡1(mod q).

证明 可参见文献［8］.

引理4 当m=1时，方程(5)仅有适合Y=Z的整数解(X，Y，Z).

证明 可参见文献［9］.

引理5 设q是奇素数，n是正整数，则方程:

仅有正整数解(X，Y，n)=(1，1，1).

证明 设(X0，Y0，n0)是方程(6)的一组正整数解.此时:

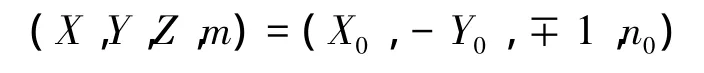
是方程(5)的整数解.根据引理3，n0≡1(mod q).令n0=kq+1(k是非负整数)，则方程(5)有整数解(X，Y，Z，m)=(2kX0，－Y0，∓1，1)适合 m=1.再根据引理4，Y0=1.于是方程(6)仅有正整数解(X，Y，n)=(1，1，1).

引理6 方程X4－2Y4=1没有正整数解(X，Y).

证明 可参见文献［7］.

引理7 设n是大于2的整数，则方程X2－2Yn=1没有正整数解(X，Y).

证明 由于大于2的整数，不是4的倍数，就是奇素数q的倍数，因此只需考虑n=4或q的情形.

n=4时，由引理2知，结论成立.

n=q时，原方程可化为:

又 gcd(X+1，X－1)=2，故存在正整数 a，b使得:

此时有 aq－2q－1bq=1.由引理 5 知，结论成立.

同样根据引理5和引理6，可证下面的引理8和引理9.

引理8 设n是大于2的整数，则方程Xn－2Yn=1没有正整数解(X，Y).

引理9 设n是大于2的整数，则方程Xn－2Yn=－1仅有正整数解(X，Y)=(1，1).

引理10 (Fermat大定理) 设n是大于2的整数，则方程Xn+Yn=Zn没有正整数解(X，Y，Z).

引理11 p为奇素数，则丢番图方程x(x+1)(2x+1)=2py2在p≢1(mod 8)时仅有正整数解(p，x，y)=(3，1，1)，(3，24，70)，(11，49，105);在 p≡1(mod 8)时的正整数解为(p，xn，yn)=(p，8t2n，2untnsn)，这里 p，un，tn，sn满足 sn+2=6sn+1－sn，s1=3，s2=17，tn+2=6tn+1－tn，t1=1，t2=6 及 pu2n=16t2n+1.

证明 可参见文献［10－12］.

3 定理1的证明

设方程(4)有正整数解(x，y，z).因为 gcd(x+1，x(x+2))=1，故存在正整数 a，b，使得:

或:

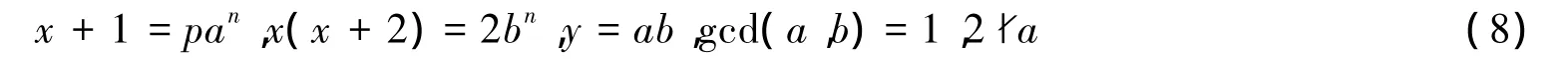
或:

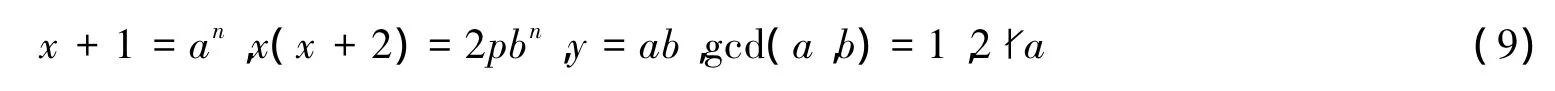
或:

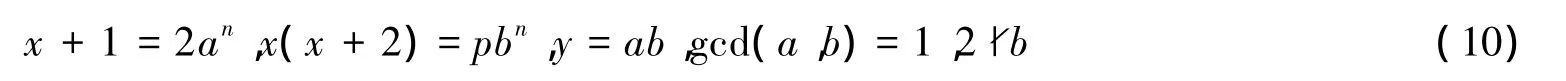
若式(7)成立，则有(2pan)2－1=bn，根据引理1，该种情形方程(4)没有正整数解.

若式(8)成立，则有(pan)2－1=2bn，根据引理7，该种情形方程(4)没有正整数解.

若式(9)成立，则由gcd(x，x+2)=2及式(9)的第二式得:

或:

或:

或:

这里 c，d 是满足 gcd(c，d)=1，2cd=b 的正整数.

将式(9)的第一式代入式(11)的第二式，得:an+1=(2d)n，由引理10知，在该情况下方程(4)没有正整数解.

将(12)的第一式代入式(9)的第一式，得:an=2cn+1，由引理8知，该情况下方程(4)没有正整数解.

将(13)的第一式代入式(9)的第一式，得:(2c)n+1=an，由引理10知，该情况下方程(4)没有正整数解.

将式(9)的第一式代入式(14)的第二式，得:an+1=2dn，由引理9知，a=d=1，此时x=0，故该情况下方程(4)没有正整数解.

若式(10)成立，则由gcd(x，x+2)=1及式(10)的第二式得:

或:

这里 c，d 是满足 gcd(c，d)=1，cd=b 的正整数.

将式(10)的第一式代入式(15)的第二式，得:2an+1=dn，由引理8知，该情况下方程(4)没有正整数解.

将式(16)的第一式代入式(10)的第一式，得:cn+1=2an，由引理 9 知，c=a=1，此时 x=1，p=3，d=1，b=1，y=1，故方程(4)仅有正整数解(p，x，y)=(3，1，1).定理1 得证.

由引理11立得定理2.最后证明定理2的推论.

由 t1=1，得:pu21=17 是素数，故 p=17，u1=1，此时方程(4)有正整数解(p，x，y)=(17，16，12).

由 t2=6，得:pu21=577 是素数，故 p=577，u2=1，此时方程(4)有正整数解(p，x，y)=(577，576，408).

由 t3=35，得:pu23=19601=17·1153，无解.

由 t4=204，得:pu24=665857 是素数，故 p=665857，u4=1，此时方程(4)有正整数解(p，x，y)=(665857，665856，470862).

由 t5=1189，得:pu25=22619537=17·241·5521，无解.

由 t6=6930，得:pu26=768398401=97·577·13729，无解.

由 t7=40391，得:pu27=26102926097=17·1535466241，无解.

由 t8=235416，得:pu28=886731088897=257·1409·2448769，无解.

由 t9=1372105，得:pu29=30122754096401=17·1009·1153·1523089，无解.

由 t10=7997214，得:pu210=1023286908188737=577·188801·9393281，无解.

由 t11=46611179，得:pu211=34761632124320657=17·2113·967724510017，无解.

由 t12=271669860，得:pu212=1180872205318713601=193·665857·9188923201，无解.

由 t13=1583407981，得:pu213=40114893348711941777=17·2359699608747761281，无解.

由 t14=9228778026，得:pu214=1362725501650887306817=577·209441·11276410240481，无解.

由 t15=53789260175，得:pu215=46292552162781456490001=17·241·1153·5521·1774998973441，无解.

由 t16=313506783024，得:pu216=1572584048032918633353217=11777·2393857·55780318173953，无解.

由 t17=1827251437969，得:pu217=53421565080956452077519377=172·25841·7153349567063158273，无解.

由 t18=10650001844790，得:pu218=1814760628704486452002305601=97·577·13729·63073·1255393·29827009，无解.

由 t19=62072759630771，得:pu219=61648439810871582916000871057=17·1217·2979768950208883122238913，无解.

由 t20=361786555939836，得:pu220=2094232192940929332692027310337=665857·3145168096064063804528641，无解.

由 t21=2108646576008245，得:pu22171142246120180725728612927680401=17·1153·37633·1535466241·62811654210817，无解.

由 t22=12290092900109634，得:pu222=2416742135893203745440147513823297=577·129835460129·32259763523421219809，无解.

由 t23=71631910824649559，得:pu223=82098090374248746619236402542311697=17·26497·284833·4534129·141124771638127729，无解.

由 t24=417501372047787720，得:pu224=2788918330588564181308597538924774401=257·1409·3457·2448769·909796961546380464769，无解.

由 t25=2433376321462076761，得:pu225=94741125149636933417873079920900017937=17·241·401·1601·5521·21532801·302983233178148401，无解.

由 t26=14182756556724672846，得:pu226=3218409336757067172026376119771675835457=577·48075457·116022453467595485290817992513，无解.

由 t27=82663163018885960315，得:pu227=109331176324590646915478914992316078387601=17·433·1009·1153·2161·644977·1523089·22703761·264889441，无解.

由 t28=481796221556591089044，得:pu228=3714041585699324927954256733618974989342977=449·665857·11988929·1036189204218496590689562241，无解.

由 t29=2808114166320660573949，得:pu229=126168082737452456903529250028052833559273617=17·5569·18097·90481·876497·928557820613597775470801，无解.

由 t30=16366888776367372354650，得:pu230=4286000771487684209792040244220177366025960001=97·577·13729·188801·201121·9393281·15638200177058824801，无解.

由 t31=95393218491883573553951，得:pu231=145597858147843810676025839053457977611323366417=17·1489·19841·50593·586273·5147205281·1898829606568065361，无解.

由 t32=555992422174934068969056，得:pu232=4946041176255201878775086487573351061418968498177=7681·1492993·431302713980890947612633357964569696769，无解.

由 t33=3240561314557720840260385，得:pu233=168019802134529020067676914738440478110633605571601=17·1153·2113·396001·967724510017·10586068985713306007688481，无解.

由 t34=18887375465171390972593254，得:pu234=5707727231397731480422240014619402904700123620936257=577·29921·651460673·507484858937618698569373022732426977，无解.

由 t35=110083691476470624995299139，得:pu235=193894706065388341314288483582321258281693569506261137=17·241·4481·5521·1535466241·1245853636565255979087989134833281，无解.

由 t36=641614773393652358999201580，得:pu236=6586712278991805873205386201784303378672881239591942401=193·665857·9188923201·5577836661177128362617195077849548801，无解.

由 t37=3739604948885443528999910341，得:pu237=223754322779656011347668842377083993616596268576619780497=17·48763660876577·269914496787930788048518982299248090651233，无解.

由 t38=21796014919919008815000260466，得:pu238=7601060262229312579947535254619071479585600250365480594497=577·323279681·393567279233·96286981375873·1075309289139593903809，无解.

由 t39=127036484570628609361001652455，得:pu239=258212294593016971706868529814671346312293812243849720432401=17·1153·1249·2359699608747761281·4469711882959366170509869987607329无解.

此时，x＞2.58×1059.故推论得证.

据此，提出如下猜想:

猜想 若p是奇素数，n=2，则方程(4)在p≡1(mod 8)时仅有正整数解:

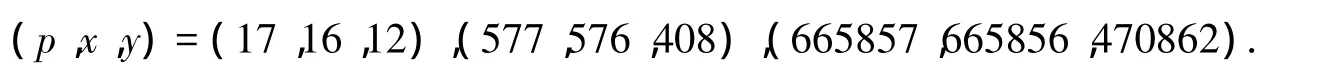
［1］ Lucas E.Problem 1180［J］.Nouv Ann Math，1875，14:336.

［2］ Ljunggren W.A diophantine problem［J］.London Math Soc，1971，3:385－391.

［3］ Watson C N.The problem of the square pyramid［J］.Messenger of Math，1981，48:1－22.

［4］ 马德刚.方程6y2=x(x+1)(2x+1)［J］.四川大学学报:自然科学版，1985(4):107－116.

［5］ 曹珍富.数论中的问题与结果［M］.哈尔滨:哈尔滨工业大学出版社，1996:124－125.

［6］ 柯召.关于方程 x2=yn+1，xy≠0［J］.四川大学学报:自然科学版，1962，14:457－460.

［7］ 曹珍富.丢番图方程引论［M］.哈尔滨:哈尔滨工业大学出版社，1989:111－112.

［8］ Ribet K.On the equation ap+2αbp+cp=0［J］.Acta Arith，1997，79:7－16.

［9］ Darmon H，Merel L.Winding quotients and some variants of Fermat's last theorem［J］.Reine Angew Math，1997，490:81－100.

［10］ 王云葵.关于丢番图方程 x(x+1)(2x+1)=2py2［J］.数学通讯，2001(5):31－32.

［11］ 管训贵.关于 Diophantine 方程 xd(n)+yφ(n)=zσ(n)［J］.湖北民族学院学报:自然科学版，2010，28(2):147－149.

［12］ 管训贵.关于不定方程 4x2n－py2=1［J］.湖北民族学院学报:自然科学版，2010，28(3):341－343.