基于数学规划法的循环冷却水网络的优化

2012-10-08沈人杰

华北电力大学学报(自然科学版) 2012年1期

冯霄，雷哲，沈人杰

(西安交通大学化工系，陕西西安 710049)

0 引言

循环冷却水作为工业用水系统中一种最重要的用水类型，其用水量占工业用水量的80%以上[1]，因此它节水状况的好坏将严重影响整个工业水系统的节水程度。由于在实际的运行中，工业循环冷却水系统存在一定数量的水蒸发消耗，同时为了避免水蒸发引起水中盐分的过度浓缩，冷却水循环系统必须有一定量的排污和补水。而补水量取决于循环冷却水的用量，所以研究如何减少循环冷却水的用量对企业有着重要的意义。

虽然不少的研究者对循环冷却水进行了相关的研究。但目前对于循环冷却水系统的研究主要集中在冷却系统的单个组成单元上[2～5]，或者是从降低循环倍率的角度考虑，而不是把系统看作一个整体，无法获得很好的节水效果。虽然也有人从水系统集成的角度进行了探讨。比如，Kim和Smith[6]将夹点的方法应用于冷却水网络的设计中，给出了循环冷却水网络的设计步骤。但水夹点的方法在处理大规模系统时较为困难，而且无法引入其他约束。相对而言，基于超结构的数学规划法处理大规模的循环冷却水系统显得更有优势。Feng等[7]将中间水道的网络结构推广到了循环冷却水网络中，并建立了相应的数学模型进行研究，但他们的研究不涉及常规的循环冷却水网络。常规的循环冷却水网络是指使用循环冷却水的冷却器构成的串联使用的水网络，这种结构的水网络具有节水量大的特点。以前的研究主要关注的是如何使用最少量的循环冷却水构造水网络，但是因为这种水网络具有不唯一性，所以如何对大规模复杂的循环冷却水网络系统进行优化，构造出用水量少、结构简单、连接数少的循环冷却水网络还需要进一步研究。

1 循环冷却水网络结构

为了方便研究，首先建立常规循环冷却水网络的超结构物理模型。对于网络中的关键单元-水冷器而言，它所需的冷却水可以是冷却塔的来水，也可以是其他任何水冷器的升温后的冷却水;它的升温后所排的冷却水，可以直接排放至冷却塔，或者也可以排至其他任何水冷器。图1为循环水网络的超结构。其中:

(1)冷却塔向S(分流节点)供水，S可以将循环冷却水分配给各水冷器;

(2)水冷器的入口M(混合节点)可以接受来自冷却塔的水及其他水冷器来的循环冷却水;

(3)水冷器的出口S可以将升温后的冷却水排向其他水冷器及排向冷却塔;

(4)返回冷却塔的冷却水向M供水，M可以接受各水冷器来的循环冷却水。

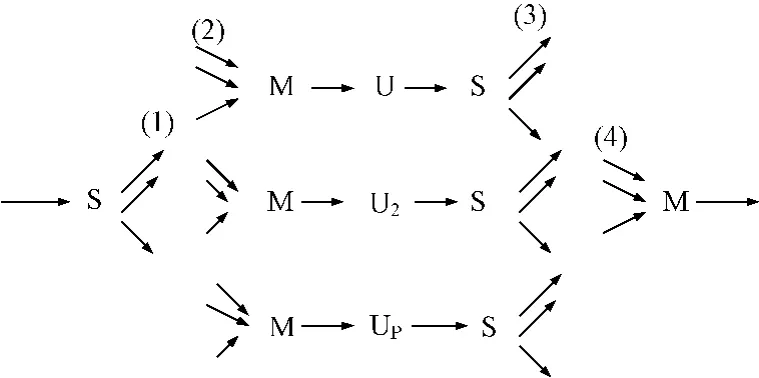
图1 循环水网络的超结构Fig.1 Superstructure of circulating water networks

图2表示一个典型的水冷器的接受排放冷却水的情况，这个图清楚地表示了这种结构水冷器的进出水情况。

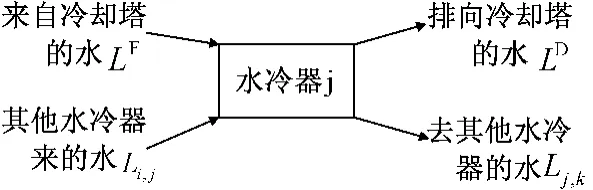
图2 典型的水冷器的进出水情况Fig.2 Inlets and outlets of a typical cooler

2 循环冷却水网络优化模型

根据循环冷却水系统的超结构模型，以及各水冷器的热容流率及水的热量平衡关系，建立循环冷却水网络优化的数学模型。模型的建立可以分为两步:首先建立以最小循环冷却水量为目标的数学模型，然后再建立以连接数少为目标值的数学模型，从而可以得到循环冷却水量小且连接数少的循环冷却水网络。需要指出的是，这里不考虑各个水冷器中的热量和水量的损失。

2.1 优化循环冷却水用量

首先以循环冷却水网络最小流率为目标值建立数学模型，求解就可获得循环冷却水网络的最小流率。为了便于计算，以循环冷却水的最小热容流率为目标值，热容流率除以比热容即为循环冷却水的流率。

P1:

目标函数:

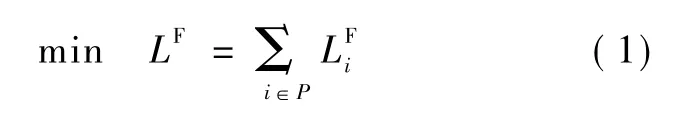
约束条件:

(1)水冷器j进出口的热容流率平衡:

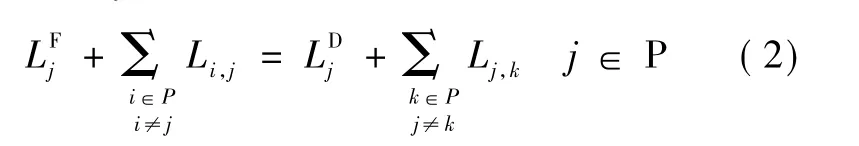
(2)水冷器j进口混合节点的热量平衡:

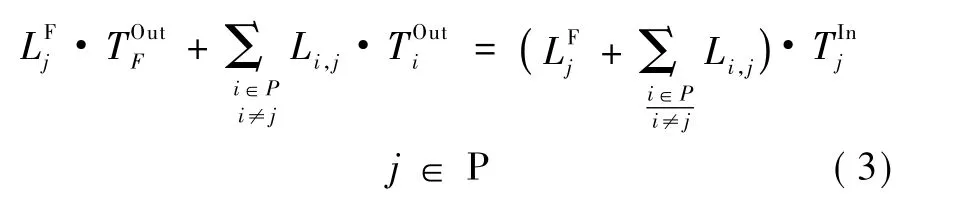
(3)水冷器j进出口的热量平衡:

(4)水冷器j进出口的温度要求:

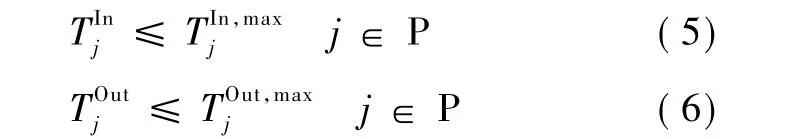
上述变量均为非负变量。

将各个水冷器的极限进出口温度及水冷器热的热容流率代入该模型求解，可以得到循环冷却水水系统的最小用水量，用LFmin来表示。

2.2 优化循环冷却水网络连接数

连接数是来自冷却塔的循环冷却水与水冷器、水冷器与水冷器、水冷器与冷却塔之间相互连接的个数的总和。也就是说循环冷却水网络的复杂性由连接数直接决定。连接数少的循环冷却水网络结构必然简单，投资费用较低。因此，用连接数最少为目标建立数学模型。

P2:

目标函数:约束条件:

约束条件同式 (2) ～ (6)

增加约束条件:

式中:

式 (8)～(10)为连接数的有关约束，如果存在连接，其中的整形变量值为1，不存在时为0。式 (11)为网络的总循环冷却水量的约束。采用相关的数学规划软件求解这个模型，就可以得到循环冷却水量小于目标值，并且连接数最少的循环冷却水网络。

3 实例研究

以某现行炼油厂为例进行研究，为了简化网络，以车间为系统分别优化。限于篇幅，本文只给出其中的重整车间的优化结果。通过对企业实际用水状况的调研可知，其现行冷却水的总流量为55 210.4 t·d－1。相应该车间的冷却水极限数据如表1所示。

表1 重整车间冷却水数据Tab.1 Circulating water data of the reforming process

将该车间的极限数据代入数学模型P1，采用Lingo软件进行求解，得出冷却水的最小流量为10 310.07 t·d－1，然后根据该最小流量和模型P2，优化获得循环冷却水网络的最小连接数为32，优化后的相应用水网络匹配图如图3所示。该车间优化后可节约冷却水44 900.33 t·d－1，占现行冷却水总量的81.3%。按该企业0.52%的补水率，直接节约233.48 t·d－1的新鲜水。按其新鲜水价格1.6元/t计算，每年可节约11.21万元(按年运行300天计)。

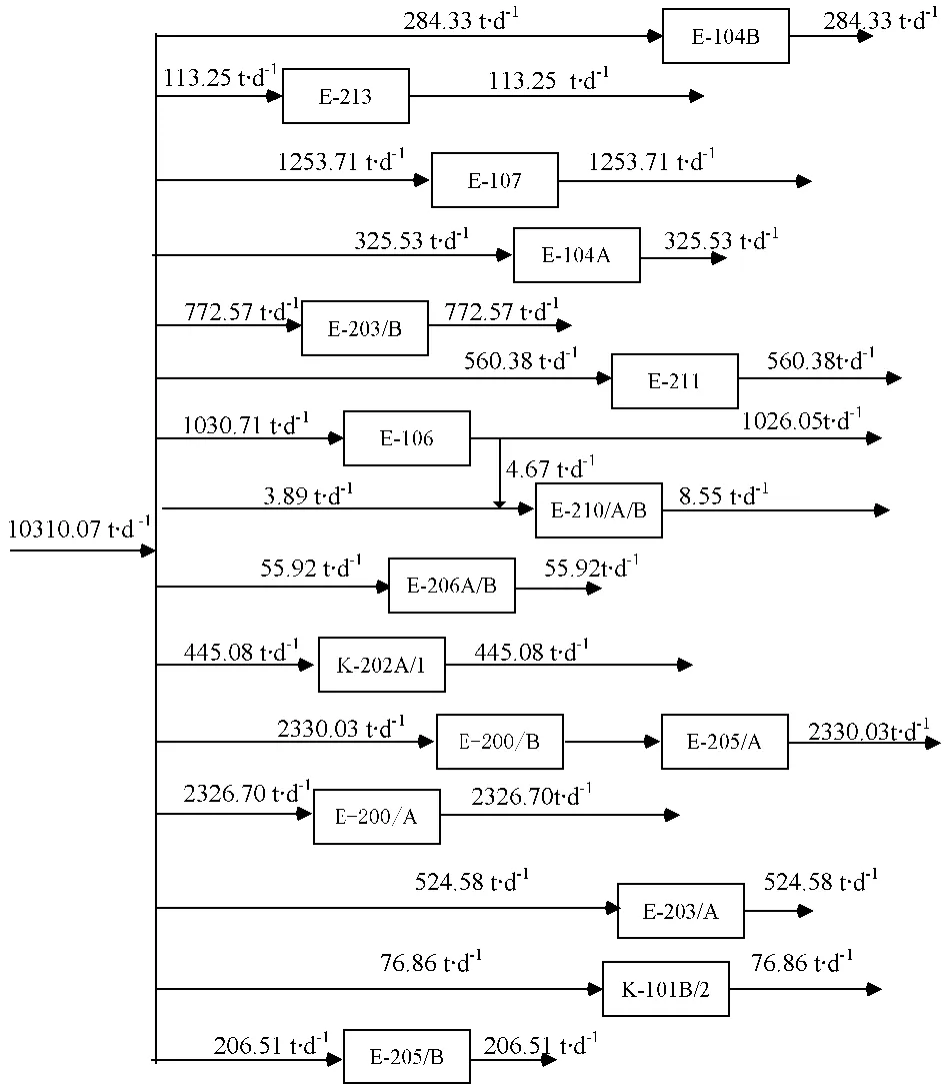
图3 优化后的循环冷却水网络Fig.3 The circulating water network after optimization

4 结论

本文采用数学规划的方法，针对工业中用量较大的循环冷却水进行研究，建立了数学模型依次对循环冷却水网络的用水量和连接数进行优化，通过求解本文提供的数学模型，可以获得一个用水量少且结构相对简单的循环冷却水网络。实际工业应用的研究表明，本文对循环冷却水优化的优化方法是可行的、有效的节水方法。特别地，当企业因扩产或新增装置需要导致循环水量不足时，可以通过采用该优化方法可以不建新的循环水系统而满足企业需求。

符号说明:

Hj——水冷器 j的热负荷/kW;

Li，j——水冷器 i提供给水冷器 j的冷却水的热容流率/kW·℃－1;

P——水冷器的集合。

TOjut——水冷器 j的出口温度/℃;

TOFut——冷却塔的出口温度/℃;

TOjut，max——水冷器j的极限出口温度/℃;

yi，j——0、1整形变量，用来描述水冷器 i是否给水冷器j提供冷却水;

U——人为取定的常数;

δ——人为取定的常数。

[1]王勤娜，施宝昌，王浩，等．工业循环冷却水缓蚀阻垢剂的发展状况[J]．化工进展，2001，20(5):26－27．

[2]Castro M M，Pinto J M，Song T W．Operational cost minimization in cooling water system[J]．Braz J Chem Eng，2000，17(4):4 －7．