两相混合式换热器瞬态工况热力学模型及应用
2012-10-08郭喜燕李爱娟杨勇平
郭喜燕,李爱娟,杨勇平
(华北电力大学 能源动力与机械工程学院,北京 102206)
0 引言
换热器是能量系统的常用设备,其类型有混合式和表面式两类。就其工质所处相态,混合式换热器有可分为单相 (汽-汽、液-液)和两相(汽-液)。两相混合式换热器在电厂回热系统中得到了广泛应用,其中最典型的是除氧器,其次还包括某些国外机组的低压加热器,并且,两相混合式换热器内进行的是综合传热和传质的强烈不可逆过程,机理最为复杂。
两相混合式换热器的稳态热力学分析方法已经成熟,近期的研究大多集中于基于传热学的传热传质分析[1],或针对具体设备进行的研究。例如,对除氧器的研究主要集中在除氧器的优化设计[2~4],而以往对除氧器的暂态研究主要集中在两个方面:一是在机组甩负荷对给水泵安全运行的影响 (主要指汽蚀)[5~8],二是对除氧器甩负荷后的凝结水、给水及除氧器水箱贮水的热焓、流量及压力变化的动态分析[9~11]。而对该类换热器瞬态工况的热力学分析,尤其是基于热力学第二定律的能量分析,尚未发现有人涉及,而分析是换热器节能的理论基础。
基于上述背景,本文从基础方程出发,建立了两相混合式换热器的瞬态工况热力学模型,并将之应用于某600 MW机组的除氧器,得到了除氧器在稳态和瞬态工况下,能量的分布情况,并进行了对比,分析了稳态和瞬态工况下能量分布的差异,及其产生的原因。
1 两相混合式换热器能量流向定性分析
从热力学第一定律角度分析,混合式换热器的入口各股流所携带能量分为三部分:一部分用于工质热存储,一小部分由于散热而损失,其余部分则随出口工质离开系统,如图1所示;相应地,从热力学第二定律角度分析,进入系统的分为系统工质存储、工质内部损失、随散热而散失的及离开系统的四部分,如图2所示。
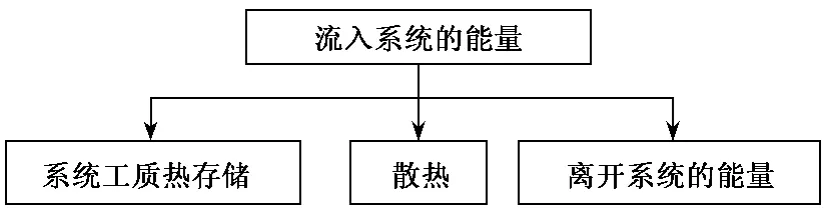
图1 系统能量分布Fig.1 Energy transfer and conversion in closed feedwater heater
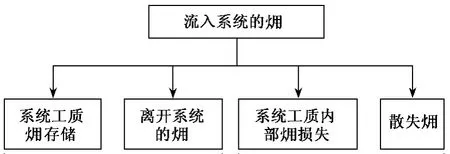
图2 系统分布Fig.2 Exergy transfer and conversion in closed feedwater heater
2 热力学模型及计算
2.1 基础方程
从基本方程出发,建立两相混合式换热器的能量分布模型。
质量守恒方程:
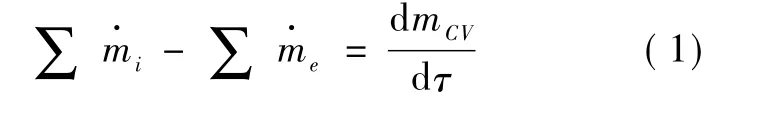
开口系能量方程:

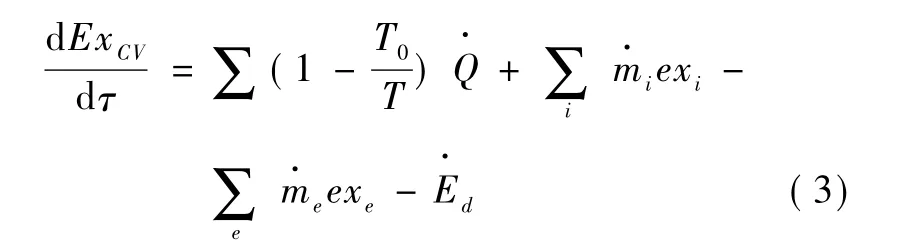
式 (1) ~ (3)中:ECV为控制体的热力学能,
·kJ;ExCV为控制体的,kJ;Q为控制体与外界换
·,kJ/kg,利用温度和压力求得;Ed为损失,kJ/s。
控制体内工质蓄热量:

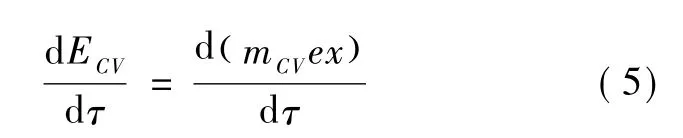
2.2 两相混合式换热器模型
质量守恒方程:

两相工质蓄热:
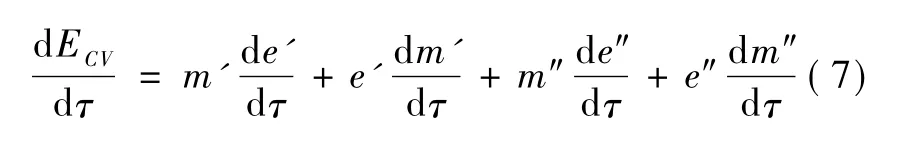
考虑到m=ρV及e=h-pv,式 (7) 变为
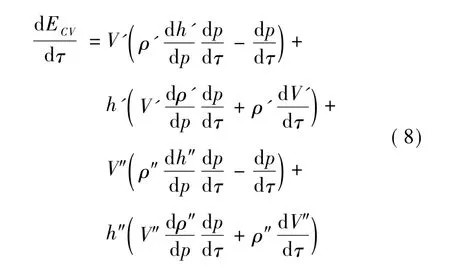
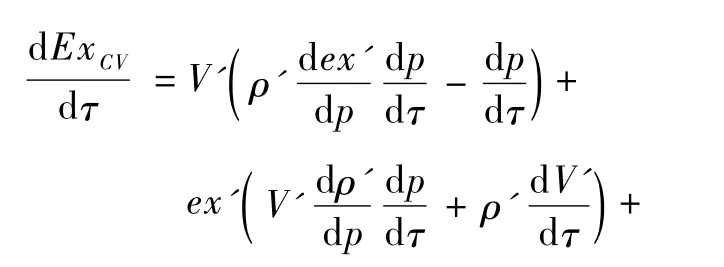

式 (6) ~ (9) 中:ρ',h',e'x分别为饱和水的密度,体积,比焓,比; ρ″,h″,e″x为饱和蒸汽的密度,比焓,比,都是通过已知的蒸汽参数求取;V',V″分别为饱和水和蒸汽的体积,从运行日志中得到水位参数,进而得到体积。
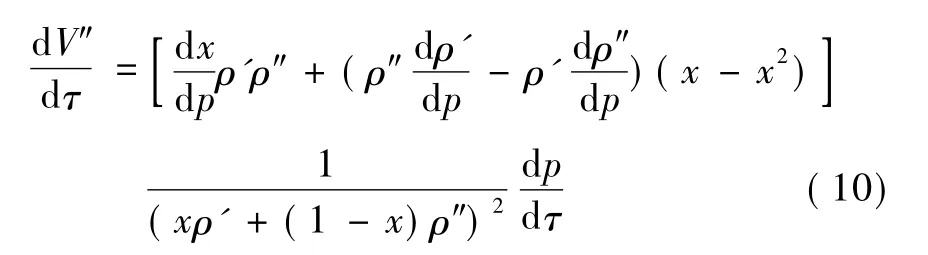
因为汽水总体积不变,所以汽部分体积变化率跟水部分体积比变化率相反,即

3 实例计算
3.1 研究对象及所用的原始数据
运用所建模型对某600 MW机组除氧器40%THA工况进行模拟。
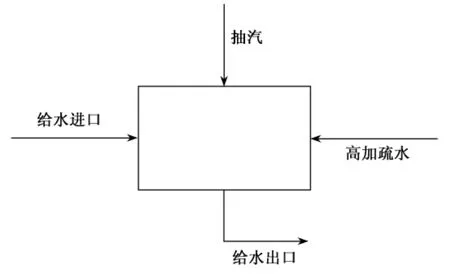
图3 除氧器示意图Fig.3 The illustration of deaerator
除氧器进口有三股流,分别为抽汽,给水进口和高加疏水,混合后由给水流出。
运用所建模型对除氧器进行模拟,模拟时采用的原始数据见表1和表2。瞬态工况变化率取0.05℃/s(即3℃/min)。
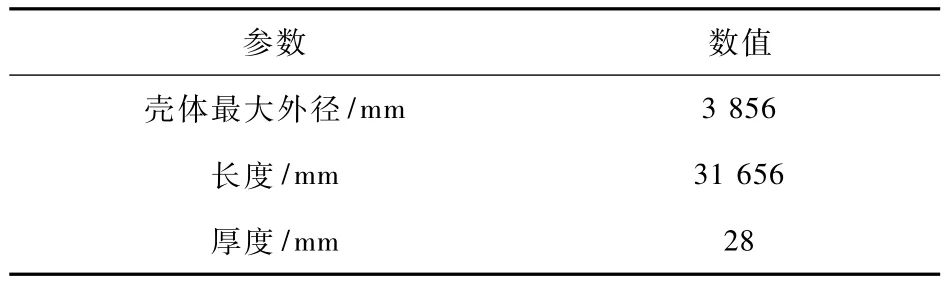
表1 结构参数Tab.1 Structure parameters
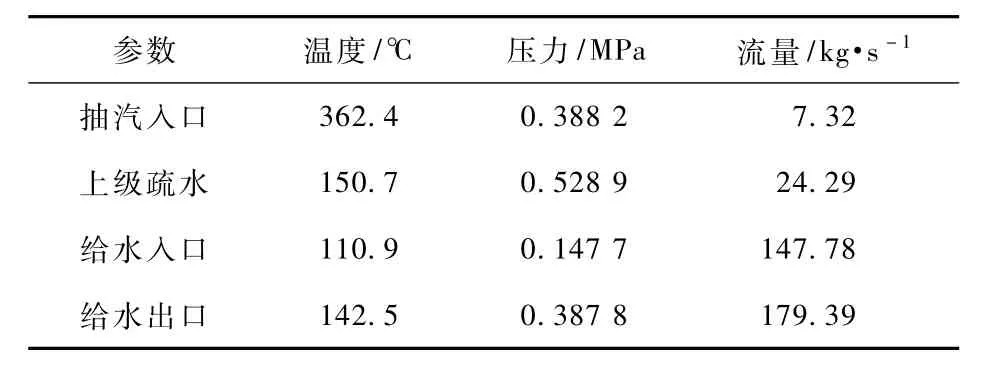
表2 工质初始参数Tab.2 Initial values of steam and feedwater parameters
3.2 计算结果汇总
为了进一步验证瞬态结果,采用稳态模型对该工况进行了计算,并将结果与瞬态结果一并展示,并对其产生的误差及原因进行分析。计算得到的能量分布情况如图4~7所示。
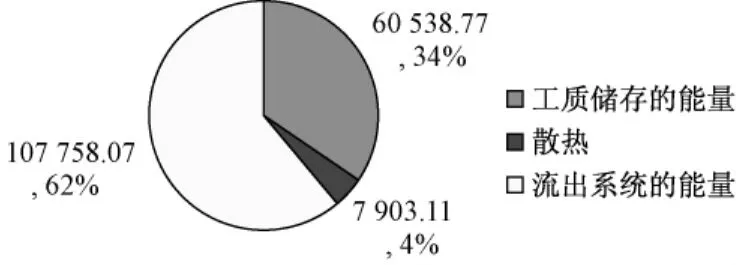
图4 除氧器瞬态热力学能分布Fig.4 Energy distribution of deaerator under transient state
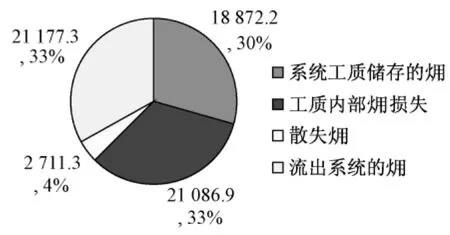
图5 除氧器瞬态分布Fig.5 Exergy distribution of deaerator under transient state
3.3 结果分析与讨论
图4是除氧器瞬态工况热力学能分布图,62%流出系统,34%由系统工质储存,剩余4%散失。图5是除氧器瞬态工况分布图,从图中可以看出,30%的由系统内工质储存,33%流出系统,33%损失在工质内部,剩余部分散失。工质蓄能部分与工质所在参数及参数变化率有关。发生在工质内部的损是由传热的不可逆性等造成的,数值上与散热量,工质的流量和压力的变化率有关。
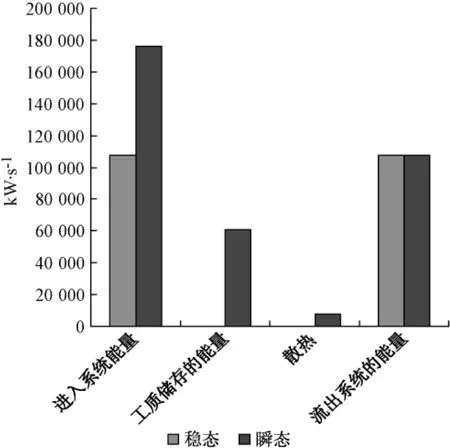
图6 除氧器稳态和瞬态热力学能分布对比Fig.6 Energy distribution of deaerator under steady state and transient state
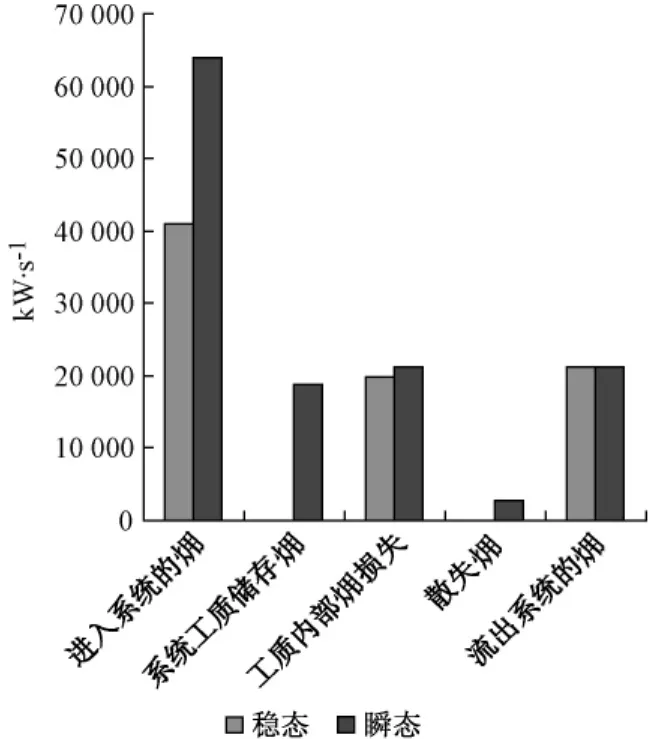
图7 除氧器稳态和瞬态分布对比Fig.7 Exergy distribution of deaerator under steady state and transient state
图6是除氧器稳态模型和瞬态模型计算的热力学能分布对比图。从图中看出:稳态模型不考虑蓄热,流入系统的能量等于流出系统的能量和散热;瞬态模型,流入系统的能量除流出系统外还有部分由系统工质储存,剩余的散失。对于散热量,采用稳态模型计算时,系统处于平衡状态散热量较小,瞬态模型中,由于系统工质内部能量变化,导致其与外部热交换量增大。
如果以稳态模型计算的热力学能分布来代替瞬态模型的分布,会存在38.8%的误差。由于稳态模型忽略了系统工质储存的能量,误差约为34.4%,其余部分误差是散热量的差异造成的。散热量的差异是因为稳态模型不考虑工质蓄热,以及发生瞬态变化时,由于参数变化导致流量变化而引起的。
发生瞬态变化时,系统工质储存部分热量,存储量的多少主要是由系统内蒸汽和水的质量变化率和单位质量的能量变化率有关。表3给出了汽、水部分压力 (温度)变化和流量变化引起的蓄热量,从表中可以看出,水部分蓄热占主要部分。对于蒸汽部分而言,流量变化的影响较大,压力变化对蓄热量的影响为负。这主要是由工质参数决定的。对水部分,压力变化引起的蓄热量大于工质流量变化引起的蓄热量,因为控制体内本身水质量很大,参数变化时引起的流量变化相对总质量来说较小。
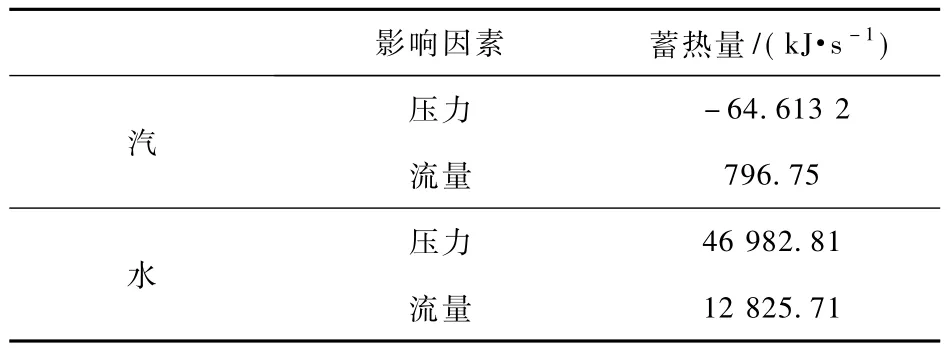
表3 不同参数变化引起的蓄热量Tab.3 Energy stored in working caused by different parameters
稳态模型计算的情况下,工质内部处于均衡,瞬态时,工质蓄能。工质储存的主要由压力,流量变化引起。表4给出了汽、水部分压力 (温度)变化和流量变化引起的蓄量。从表中可以看出系统工质储存的主要集中在水部分,主要原因是系统内水的质量远大于蒸汽的质量。对于单位质量的能量变化率,蒸汽比水大,但相对于质量上的差距,影响不大。对于蒸汽部分,流量变化占主要部分,压力对蓄量的影响为负,这主要是由蒸汽参数决定的。
表4 不同参数引起的蓄量Tab.4 Exergy stored in working caused by different parameters
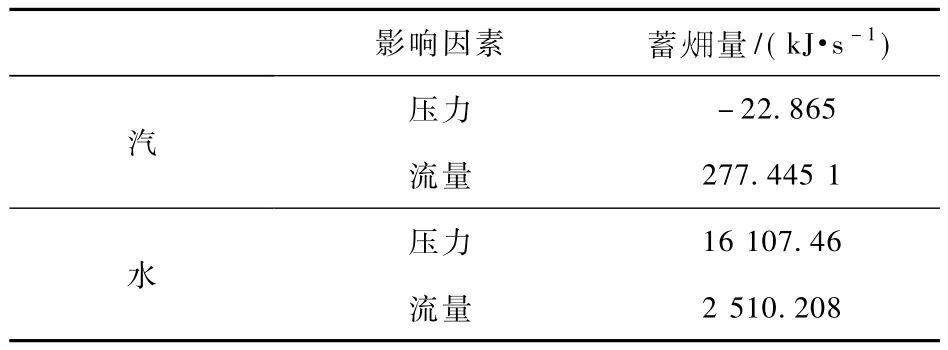
表4 不同参数引起的蓄量Tab.4 Exergy stored in working caused by different parameters
影响因素 蓄量 /(kJ·s-1)汽 水压力 -22.865流量 277.445 1压力16 107.46流量2 510.208
4 结论
应用本文所建立的混合式混热器的热力学模型对某600 MW机组除氧器进行了的研究,得到了除氧器的热力学能和的分布图,并将稳态和瞬态工况下的热力学能分布和分布进行了对比,得到的结论如下:
(1)从能量分布百分比上看出,进入系统的能量除流出系统外,主要由工质存储。在分布中,工质内部损也占有较大比例。
(2)对比系统稳态模型和瞬态模型计算的能量分布,可以看出主要差别在于进入系统的能量和工质储存的能量上。散热损和工质内部的损失也有差距。
[1]邹晓超.多元混合工质相平衡及传热模拟与系统试验研究[D].武汉:华中科技大学,2008.
[2]何雨花,张华封,华进.220MW机组卧式除氧器的设计优化[J].电站辅机,2008,12(4):6-9.
[3]王坚.除氧器布置优化及暂态计算方法[J].电力建设,2006,27,(9):41-44.
[4]戴月,李吉泉.除氧器的滑压运行[J].林业科技情报,2004,36,(2):48-49.
[5]刘建强.印度瓦罗拉电厂除氧器暂态计算[J].科教前沿,2010,(27):52-54.
[6]张晓玲.600MW火电机组除氧器暂态过程分析[J].广东科技,2007,(7):68-69.
[7]郑军,王萍.600MW机组除氧器暂态计算[J].电力设备,2006,7(10):50-52.
[8]卓宁.除氧器滑压运行暂态过程分析与计算[A].广西电机工程学会第七届青年学术交流会论文集[C].中国广西南宁.2002:318-326.
[9]邹罗明,范永春.除氧器暂态计算影响因素探讨[J].电力建设,2010,31(11):102-105.
[10]蓬静欣,邓祖诚.除氧器滑压运行暂态过程及给水泵汽蚀余量降落值的计算[J].热力发电,1987,(6):1-10.
[11]高璞珍,邢永辉,庞凤阁.小型热力除氧器传热计算[J].哈尔滨工程大学学报,1999,20(6):29-35.
[12]沈维道,蒋志敏,童均耕,等.工程热力学[M].北京:高等教育出版社,2001.
[13]Moran M J,Shapiro H N.Fundamentals of Engineering Thermodynamics[M].New York:John Wiley &Sons,2006.
