均匀壁面热流下太阳能腔式吸热器的自然对流数值模拟

吴双应，贾 丹，肖 兰，李友荣

(重庆大学 动力工程学院，重庆 400044)

0 引言

太阳能腔式吸热器是太阳能热利用系统中太阳辐射能向热能转换的关键部件，其性能和热效率的改善对提高整个系统的热电转换效率具有重要的意义。Paitoonsurikam 和 Lovegrove[1，2]在腔体壁温恒定的条件下研究了倾角、开口率和壁温等因素对圆柱形腔式吸热器内自然对流的影响。文献[3，4]对在定热流边界条件下开口向上的矩形腔内的传热特性进行了二维数值模拟;Goutam等[5]采用有限元法对开口矩形腔体分别在定热流和定壁温热边界条件下的腔体内的传热特性进行了二维数值模拟。Walid[6]对一侧全开的倾斜方形腔体在不同壁面处于定热流边界条件下的传热特性进行了实验研究。

现有文献对圆柱形腔式吸热器自然对流特性的研究大多是在腔体壁温恒定的热边界条件下进行的，然而采用实验的方法进行研究时所采用的热源大多为电加热方式，考虑到电加热的定热流特征，这就产生了实验研究与数值研究热边界条件的不一致性，从而造成两者研究结果的差异。再者根据太阳能辐射热流的特性，定热流的近似更符合实际[7～9]。另一方面，现有文献在数值模拟时大多忽略了工质变物性对自然对流的影响，特别是对高温腔式吸热器，这样的处理可能会造成数值模拟与实验结果不能很好地吻合。本文同样采用文献[1]中的圆柱形腔式吸热器为研究对象，对实际应用较多的开口朝下的吸热器腔体在均匀壁面热流边界条件下的自然对流特性进行三维数值模拟。本研究在理论上可以丰富和发展碟式太阳能热发电系统中高温腔式吸热器的自然对流传热特性研究;在工程应用上，可以用来预测在某一自然对流热损失下的吸热器腔体壁面的平均壁温;同时结合腔体内的空气温度场和流场，为加工制造腔式吸热器时材料的选择和腔体设计提供了基本理论依据。

1 物理数学模型和数值模拟方法

图1为腔式吸热器的物理模型。吸热器一侧全开，壁面由不锈钢制成，直径D=70 mm，腔体壁厚d=3 mm，高度H=150 mm，外表面覆盖一定厚度的保温层。考虑到腔体内的空气流动由层流转化为紊流的临界Ra随几何形状和边界条件的不同而不同。本文拟采用RNG k－ε紊流模型进行计算。假定吸热器内空气的流动为定常可压缩流动，其张量形式的控制方程如下:

连续方程:

动量方程:

能量方程:

图1 腔式吸热器的物理模型Fig.1 Physical model of cavity receiver

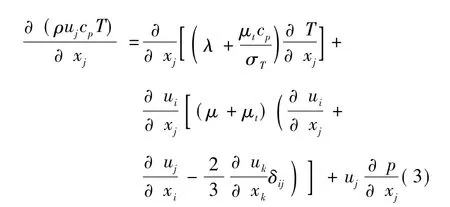
κ方程:

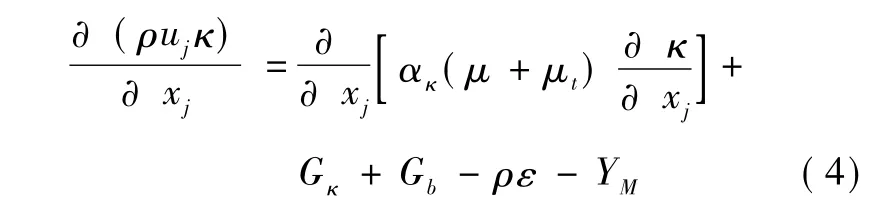
ε方程:

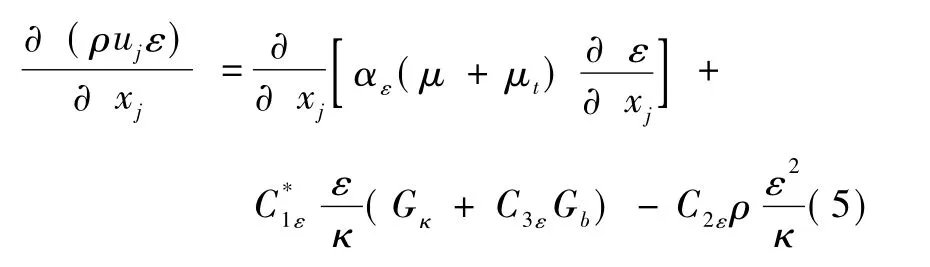
式中:ρ为空气密度，kg/m3;ui，uj，uk分别表示i，j，k方向上的速度分量，m/s;p为压力，Pa;μ为空气的动力粘度，kg/(m·s);μt为湍动黏度，kg/(m·s);gi为重力加速度g在i方向上的分量，m/s2;δij为克罗内克尔算子;κ为湍动能项，m2/s2;ε为湍流耗散率，m2/s3;λ为空气的导热系数，W/(m·K);cp为空气的定压比热容，J/(kg·K);T为温度，K;产生项 Gk、Gb和 YM， 常 数 项 C1ε、C2ε、C3ε、 σT、αk、αε和函数项 C*1ε的取值及定义见文献[10]。

考虑到定热流边界条件下腔体壁面导热对腔体内自然对流的影响，本文拟采用现有文献较少应用的腔体内壁面与空气的流固耦合方法来进行处理。实际工程中吸热器常被无限大的大气层所包围，为模拟这种环境，假设吸热器被置于一个直径和高度是自身直径40倍的圆柱形腔体中。采用非均匀网格对计算区域进行划分，在吸热器腔体内部区域以及壁面采用细密网格而在吸热器外壁面与模拟大气层的圆柱形腔体壁面之间的区域采用渐疏网格。在计算过程中暂不考虑辐射影响。

在吸热器倾角 φ为0°，壁面热流密度 q为1 000 W/m2时进行了网格无关性验证，监测了采光口所在截面圆心的温度Ta，以及腔体内壁面的平均温度 Twall，m，结果如表1所示，最终决定选择网格数为851 482的网格进行计算。

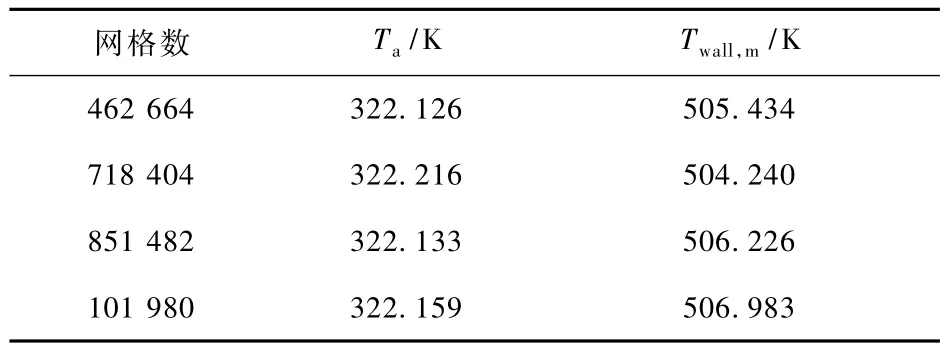
表1 网格无关性验证Tab.1 Grid dependency test results

为验证本文所采用模型的可靠性，首先对文献[6]中的一个一侧全开的方形腔式吸热器进行了三维数值模拟。其中，边界条件、几何尺寸均按上述文献中的取法，物性参数按变物性处理。将数值模拟所得的Num与文献实验所得的Num进行了比较，如表2所示，结果表明，Num随倾角的变化趋势与文献[6]一致，考虑到实验误差以及各种不确定因素的影响，除倾角为0°外，误差大多在15%以内，说明本文计算模型是可靠的。

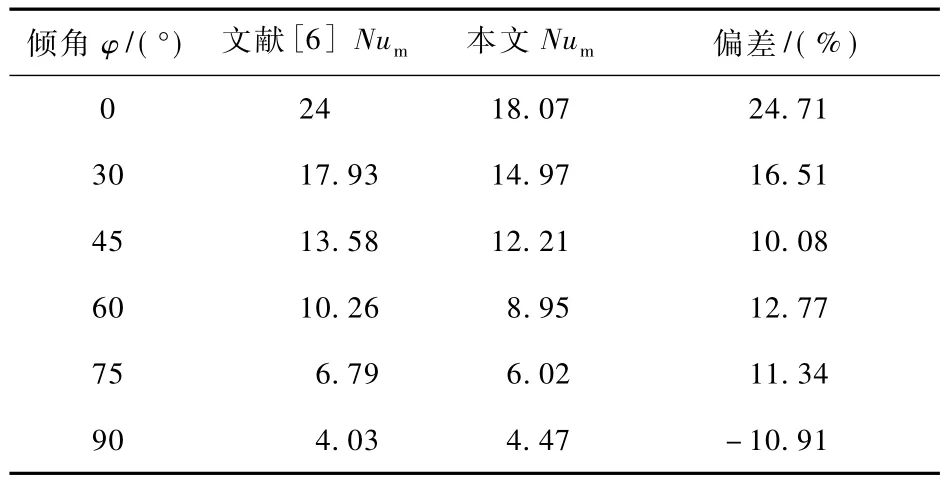
表2 本文模型与文献[6]实验结果的比较Tab.2 Comparison of presented calculation with experimental results in Ref．[6]

2 结果分析与讨论

图2给出了在腔体侧壁和底面热流密度为500 W/m2下，倾角 φ=0°，30°和60°时对称中心面的温度分布云图和腔体采光口截面的速度等值线图。从图中可以看出，当φ=0°时，吸热器腔体下部空间由于冷空气进入使得温度较低，上部空间由于空气受到壁面加热使得温度升高，且由于滞止区的存在，越靠近上壁面的区域温度越高。受热空气从采光口离开吸热器后由于外部空气的冷却，使得流出空气的温度逐渐降低。同时，随着倾角的增大，滞止区逐渐扩大，因此在腔体上部的高温区域也逐渐增大。图 (d) ～(f)表示采光口截面法线方向上的速度等值线。以进入采光口的速度为正，流出速度为负。从图中可明显看出冷空气从采光口下部进入，上部流出，由于外部冷空气粘滞力的作用，使得流出速度逐渐减小。

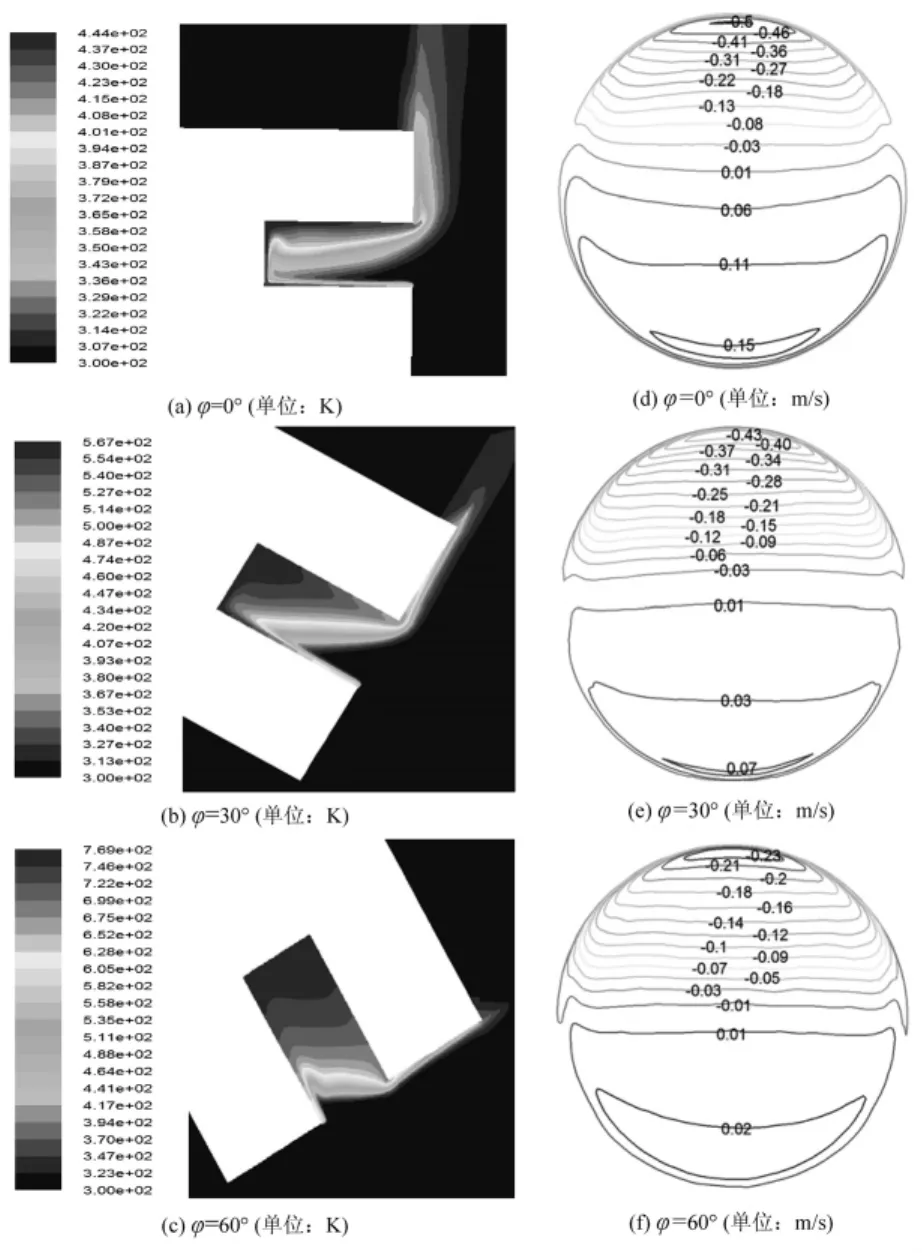
图2 不同倾角下q=500 W/m2时，中心对称面的温度分布云图 (a) ～ (c)和采光口截面的速度等值线 (d) ～(f)Fig.2 The temperature contours(a)～(c)and velocity contours(d) ～ (f)in the aperture crosssection for q=500 W/m2and different tilt angle

图3(a)给出了在φ=0°，q=500 W/m2时离采光口距离分别为 l=50 mm，100 mm，150 mm处所在截面上的温度分布云图，图中黑圆圈表示腔体内壁与空气的分界面。从图中可看出，由于腔体上部滞止区的存在，高温气体滞止，温度最高;下部由于不断有冷空气的进入使得温度最低;且随着l的减小，腔体内的空气平均温度减小。图3(b)给出了对应截面周向上的内壁面温度变化。从图中可看出，距离腔体底面越近，周向截面上的温差越小，其中在周向角θ为+90°时壁面温度最低，－90°时温度最高;并且在吸热器腔体的上半区域，壁面温度随周向角θ增大而下降的曲线呈凸形，而在吸热器腔体的下半区域，该曲线则呈凹形。

图3 l=0 mm，50 mm，100 mm和150 mm所在截面的温度分布云图 (a)和对应周向上的壁面温度变化(b)Fig.3 The temperature contours(a)in the cross-sections of l=0 mm，50 mm，100 mm and 150 mm，and circumferential wall temperature variation in corresponding cross-sections(b)

图4为腔体壁面上不同位置处的温度Twall沿轴向上的变化，由于对称性，只给出了一半腔体壁面相应位置的温度分布。图中a～e分别表示腔体壁面上的所在位置。从图中可以看出，随着离采光口距离l的增大，壁面温度升高，并且近似呈线性规律，特别是在腔体的下面一半区域。另外，随着l的增大，不同位置的壁面温差减小，但减小的幅度不大，如从l=0 mm变化到l=150 mm时，其对应的温差由28.06 K降到11.34 K。这也就说明尽管离采光口较近区域腔体壁面的温度较低，但热应力较大。

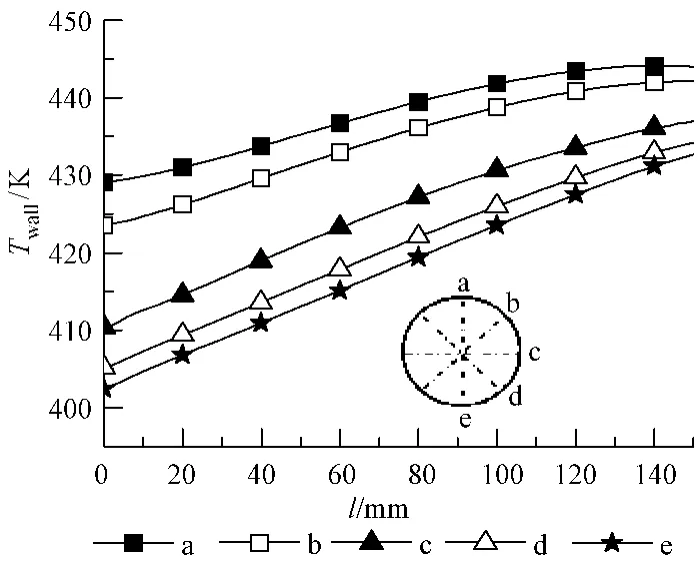
图4 腔体壁面上不同位置处的温度沿轴向上的变化Fig.4 Variations of wall temperature at different axial locations on the receiver wall

图5给出了在不同倾角不同热流时对应的平均努塞尔特数Num的变化规律，其中努塞尔特数的特征长度取腔体内径 D，环境温度为300 K。从图中可看出，在一定倾角下，随热流密度增加，Num增加;在同一热流下，Num随倾角的增加而减小，且随着倾角的增大，不同热流密度下的Num差异减小。

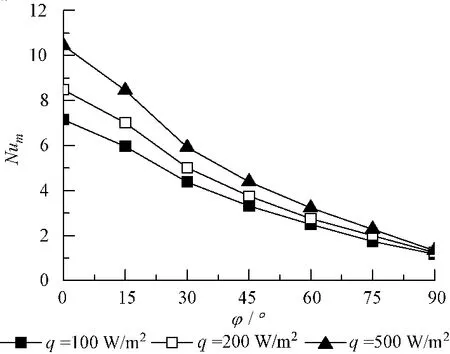
图5 不同热流密度q下Num随倾角φ的变化Fig.5 Variation of Numwith φ at different wall heat flux q

3 结论

在考虑变物性以及腔体内壁和空气流固耦合的基础上，对一个圆柱形太阳能腔式吸热器在均匀热流边界条件下的自然对流特性进行了三维数值模拟。主要结果如下:

(1)随着腔体壁面热流密度增加，内壁面上平均温度将升高，平均努塞尔特数增加;随着吸热器倾角的增大，平均努塞尔特数减小。

(2)随着离采光口距离的增大，腔体壁面温度近似呈线性规律升高，特别是在腔体的下面一半区域;并且同一截面不同位置处的壁面温差减小，但减小的幅度不大。

(3)对同一截面，在吸热器腔体上半区域，壁面温度随周向角θ增大而下降的曲线呈凸形，而在吸热器腔体的下半区域，该曲线则呈凹形。

[1]Paitoonsurikarn S，Lovegrove K．Numerical investigation of natural convection loss in cavity－type solar receivers[C]．Proceedings of 40th Conference of the Australia and New Zealand SolarEnergy Society(ANZSES)，Newcastle，Australia，2002.

[2]Paitoonsurikarn S，Lovegrove K．Numerical investigation of natural convection loss from cavity receivers in solar dish applications[J]．Journal of Solar Energy Engineering，2011，133(2):1－10．

[3]Polat O，Bilgen E．Laminar natural convection in inclined open shallow cavities[J]．International Journal of Thermal Sciences，2002，(41):360－368.

[4]Polat O，Bilgen E．Natural convection and conduction heat transfer in open shallow cavities with bounding walls[J]．Heat and Mass Transfer，2005，(41):931－939.

[5]Goutam S，Sumon S，Arif HM．A finite element method for steady－state natural convection in a square tilt open cavity[J]．Engineering and Applied Sciences，2007，(2):41－49.

[6]Walid C．Effect of boundary wall conditions on heat transfer for fully opened tilted cavity[J]．ASME Journal of Heat Transfer，2004，(126):915－923.

[7]Bilgen E．Passive solar massive wall systems with fins attached on the heated wall and without glazing[J]．Journal of Solar Energy Engineering，2000，(122):30－34.

[8]Stephane A，Patrice C，Gilles F．Design and simulation of a solar chemical reactor for the thermal reduction of metal oxides:case study of zinc oxide dissociation[J]．Chemical Engineering Science，2007，(62):6323－6333.

[9]Wang M，Siddiqui K．The impact of geometrical parameters on the thermal performance of a solar receiver of dish－type concentrated solar energy system[J]．Renewable Energy，2010，35(11):2501－2513.

[10]张师帅．计算流体动力学及其应用—CFD软件的原理与应用[M]．武汉:华中科技大学出版社，2011.