近世代数教学的探索与实践
2012-10-08龙述德
龙述德
(重庆文理学院数学与财经学院,重庆 永川 402160)
近世代数是以研究代数系统的性质与构造为中心的一门学科,它不仅是现代数学的重要基础,也是许多其他现代科学的基础,已成为数学专业本科生的重要基础课之一.掌握近世代数的基本概念、理论和方法也是每一位数学工作者所必需的基本数学素养之一.
近世代数又名抽象代数,其内容具有高度的抽象性和概括性,这使得它不同于其他数学学科.许多学生感到这门课程非常抽象、生涩难懂、不直观,因此他们很难具备用近世代数的基本思想和理论来解决具体问题的能力,从而直接影响后续课程的学习热情.笔者根据多年的教学经验,认为应该注意几个方面.
1 上好第一节课,激发学生的学习热情
俗话说,好的开始等于成功的一半.因此,上好第一节课对学生学好近世代数是很重要的.教师在第一节课不要急于上新课,在讲述课程的研究对象之后,接下来可以介绍近世代数产生的数学背景[1-2].从一般一元 n次方程 anxn+an-1xn-1+… +a0(an≠0)的求根问题,引出法国青年数学家伽罗华(Galois)及其著名的伽罗华理论、挪威青年数学家阿贝尔(Abel)等,并介绍他们一生的一些典型的故事和他们对近世代数课程的发展所做出的杰出贡献,这样会让学生对数学天才伽罗华和阿贝尔产生景仰,从而激发他们的学习热情.紧接着,可以讲近世代数研究的意义,并用具体的例子来说明研究其意义所在.近世代数是现代物理学、化学、生物学、密码学等不可缺少的工具,例如:晶体结构分类,对称性匹配的分子轨道,DNA序列的对称性,编码理论(尤其是纠错码)等,都要用到近世代数的理论和方法.还可进一步告诉学生,有志于在现代科学技术方面有所贡献的年轻人,懂得近世代数的知识是非常必要的.这样,可使学生明白近世代数确实是有用和具体的,进而引起他们学习的兴趣.最后,为了保证学生把这门课程学好,还需告诉他们一些正确的学习方法及注意事项.
2 重视基本概念教学,提高学生的思维能力
概念是浓缩的知识点,是思维的细胞.教师在近世代数概念教学中重视培养学生分清实质的能力及培养学生思维的深刻性,是非常重要的.这种能力表现为能洞察所研究事物的本质及其相互联系;能从所研究的材料中揭示被掩盖的特殊情况,并且能组合各种具体模式等.教师在概念教学实践中,应力求通过对比、联想概念之间的异同,找出每个概念的特点并挖掘出其关键所在.例如,元素的阶和群的阶[3-4].元素的阶是指对群G中元素a来说,使得am=e的最小正整数m.若这样的m不存在,则a的阶是无限的;而群的阶是指群所含元素的个数,从定义来看,它们有本质区别,但在学习中学生又很容易混肴.因此,在讲解过程中应让学生仔细观察后教师再指出前者的关键所在是“am=e的最小正整数m”,而后者的关键是“元素的个数”.这样就抓住这两个概念的本质,培养了学生洞察事物本质的能力.还可以举模6的剩余类加群Z6来加以说明并指出它们的联系,从而为讲后面的指标定理打下基础.
3 加强直观性教学,力促学生实现由形象思维到抽象思维的转化
数学的基本属性之一是抽象.然而,数学教学又要求把抽象的东西形象化,通过直观的形象来深化抽象的内容[5].这种抽象中的形象,正是数学教学的真缔.教师在教学中应多举实例,注重与高等代数知识及中学数学知识相联系[2],为近世代数教学建立起形象的数学模型.这是帮助学生转变思维方式的关键一步.学生经过初等数学及高等代数等数学专业课程的学习,他们头脑中形象的东西比较多,基本功也比较扎实,并且也具有一定的抽象思维基础.这为他们理解近世代数中的高度抽象概念和一般性的理论提供了形象的实例.这不仅有利于高度抽象概念的理解,而且也能从较高的层次对初等数学和高等代数所学的知识内容给予科学的解释.例如,等价关系是一个比较抽象的内容,可以中学实数集合中的等于关系及高等代数中的矩阵合同关系为例来说明它们都是等价关系.这样就显得比较直观,并把不同的数学对象统一起来,进而加深学生对等价关系的理解.另外,在高等代数的学习中,学生遇到过矩阵方程AX=B的求解,若是在可逆矩阵集合中求解,方程只有唯一的解,而在一般方阵集合中,方程却可以只有一个解、无数个解甚至无解的情况,当时不知其所以然.在学习近世代数群论概念后适时提出该问题,让学生尝试用群论知识进行解释,这会让学生心中豁然开朗,促进他们从形象思维到抽象思维的转化.
4 讲究课堂提问技巧,激发学生的思维
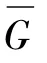
5 结语
近世代数是一门高度抽象的数学学科,对数学专业的本科生而言是比较难学的.虽然笔者结合多年教学经验,提出了近世代数课程教学的一些做法,但仍然不够成熟,在实际教学中也还会有新的问题不断涌现.这需要我们根据具体情况,适时进行教学方法的调整和改进.
[1]刘绍学.谈谈“近世代数”这门课[J].高等数学研究,2000,3(3):8-9.
[2]赵静,周卫,刘振海.近世代数课程教学的几点建议[J].广西民族大学学报:自然科学版,2010,16(3):94-96.
[3]张禾瑞.近世代数基础[M].北京:高等教育出版社,1978:34-37.
[4]吴品三.近世代数[M].北京:高等教育出版社,1979:61-63.
[5]冯克勤.高校代数课教学的一些做法和看法[J].大学数学,2004,20(5):5-7.
