一类非线性双曲方程的整体解
2012-10-08严勇
严 勇
(四川民族学院数学系,四川 康定 626001)
本文研究如下一类非线性双曲方程的初边值问题:

其中:Ω⊂Rn(n≥1)是具有光滑边界∂Ω的有界区域,γ ≥0,δ≥0,β > 0,α,β,γ 均为常数.方程(1)被称为带耗散项和强阻尼的Kirchhoff方程.一般我们作如下的假设:
(H1)m(s)∈C1([0,+∞)),且存在常数m0,使得对任意的s≥0有m(s)≥m0≥1;

当γ=0,δ=0,β=0时,此方程解的存在性被许多作者研究过[1-2].当 n=1,m(s)=a+bs(a,b > 0) 时,Kirchhoff G[1]在1883 年研究弦的横截运动时,提出如下的数学方程,即:
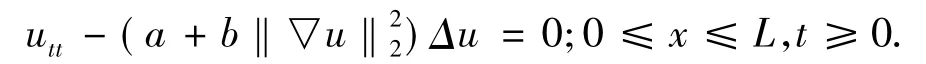
其中:L表示弦的长度.当γ=0,δ=0,β=1时,文献[4]利用Galerkin方法和势井理论得到了方程局部解的存在性与唯一性.当δ=0时,文献[5]利用Galerkin方法和势井理论,得到了在小初值条件下,局部解的存在性与唯一性.当m(s)=1时,其研究结果可见文献[6-7].陈冬贵[8]研究了具有Lipschitz连续系数的非齐次kirchhoff方程的Cauchy问题.
本文考虑的函数都是实函数,当不引起混淆时,我们略去 u(x,t),ut(x,t) 中的 x,并分别记为u(t),u'(t).当2≤p≤∞ 时,记‖·‖p为Ω上Lp的范数.特别地,L2(Ω)上的范数和内积分别记为‖·‖2和(·,·).由于方程(1)中含有常数 α,β,γ,文献[4]和[6]构造的能量泛函不适合该问题(1)~(3).我们将构造新的能量泛函,引进稳定集的概念,利用Galerkin方法和改进的势井理论,得到问题(1)~(3)解的局部存在性.
1 预备知识
首先,定义如下的能量泛函:

这样初始能量泛函为:
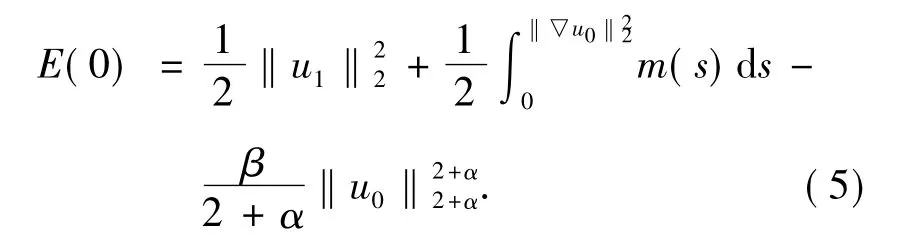
构造函数


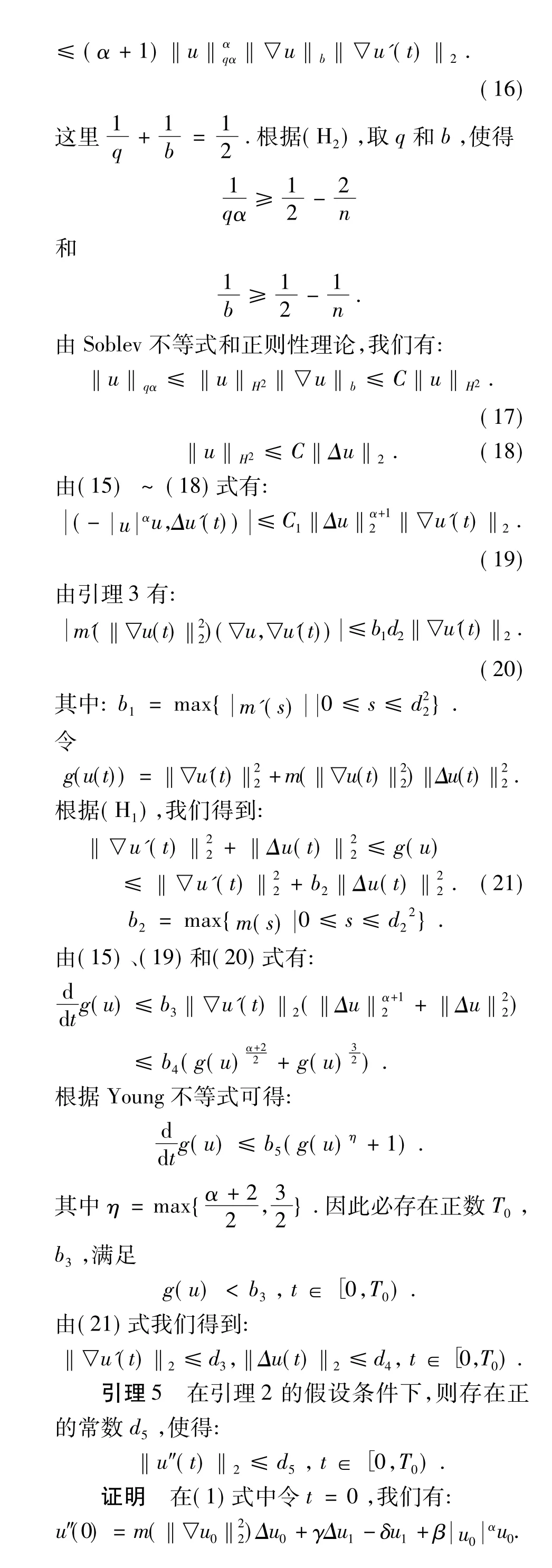



[1]Kajitani K,Yamaguti K.On global real analytic solutions of the degenerate Kirchhoff equation[J].Ann.Sc.Sup.Pisa,1994(4):279-297.
[2]Hirosa F.Global solvability for the degenerate Kirchhoff equation with real-analytic data in Rn[J].Tsukuba J.Math.,1997(21):483-503.
[3]Kirchhoff G.Vorlesungen über mechnik[M].Teubner,Leipzig,1883.
[4]李庆霞.一类非线性双曲方程的局部解存在性[J].数学研究,2002(2):175-180.
[5]严勇,姚莉.一类非线性双曲方程的局部解[J].四川师范大学学报:自然科学版,2004,27(5):497-500.
[6]Todorova G.Stable and unstable sets for the cauchy problem for a nonlinear wave equation damping and source terms[J].J.Math.Anal.Appl.1999,239:213-226.
[7]Todorova G.Cauchy problem for a nonlinear wave equation with nonlinear damping and source terms[J].Nonliear Anal.,2000,41:891-905.
[8]陈冬贵.具有Lipschitz连续系数的Kirrchhoff方程[J].数学学报,1998,41(2):337-346.
