全平均曲率的一阶变分问题

张 霞，张 卓

(云南师范大学数学学院，云南 昆明 650092)

变分法是为了解决实践中的极值问题而产生的，在微分几何中，长度、体积、曲率的重要性使得变分法成为一个有力的工具，它研究的是函数的极值问题，即通过对未知函数的积分及其导数来构造．变分的最终目的是寻求使泛函取得极大值或极小值的极值函数，在微分几何中，我们常借助变分法来求解边界值问题．

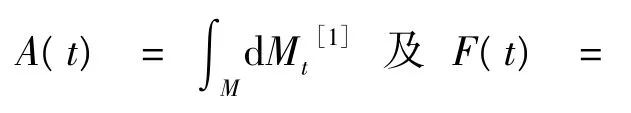
1 预备知识

首先，我们给出子流形中变分问题的一些基本概念：

则称F为f的一个变分．

定义2［1］若设Mn中沿f(M)的向量场为：

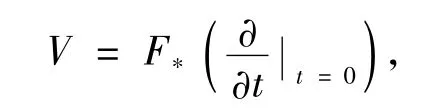
则称V为f的变分向量场．

令变分向量场

其中：ai，aα是变分向量场的分量，且 aAB=-aBA．

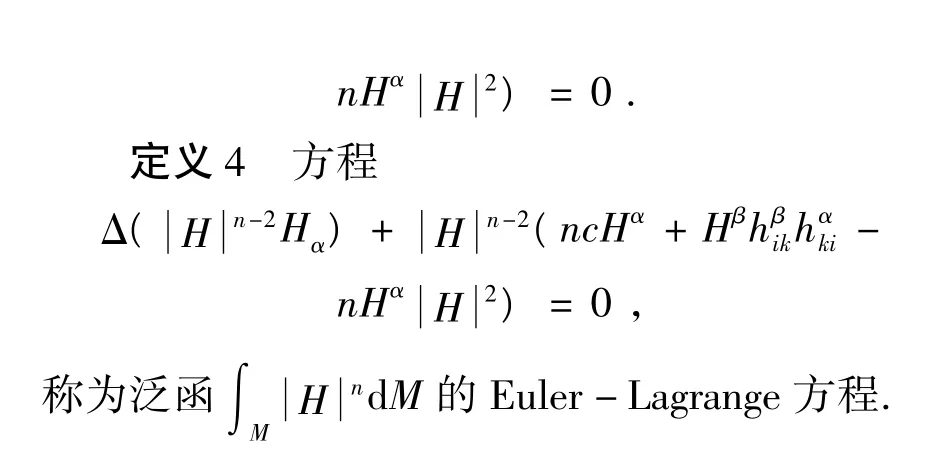
3 结论

［1］陈维桓，李兴校．黎曼几何初步［M］．北京：北京大学出版社，2002：358-425．

［2］王换清，吴发恩．R3中环面的变分性质［J］．北方工业大学学报，2008，20(3)：52-55．

［3］Hu Z J，Li H．Willmore submanifolds in Riemanifolds［J］．Proceedings of the Workshop，Contem．Geom．and Related Topics，World Scientific，May，2002：251-275．