基于激光跟踪仪的机器人误差测量系统标定*

齐立哲 陈 磊 王 伟 余蕾斌 贠 超

(①北京航空航天大学机器人研究所，北京 100083;②上海飞机制造有限公司，上海 200436)

一般工业机器人重复定位精度很高，但绝对定位精度很差。为了提高机器人的性能及拓展工业机器人的应用范围，需要对机器人运动学模型的参数进行标定来降低它的绝对定位误差。机器人标定一般分4个步骤进行:建模、测量、辨识与补偿［1］。为了测量出机器人在其工作空间内的各个测量点的定位误差，需要对测量靶标中心在机器人末端的位置(工具坐标系)及机器人基坐标系与测量设备坐标系之间的转换矩阵(基坐标系)进行标定，以将直接从机器人中获取的末端法兰盘中心测量数据与测量设备测得的靶标中心的数据统一到一个坐标系下。因此在工业机器人定位误差测量过程中涉及到机器人工具坐标系及基坐标系标定的问题。

针对机器人工具坐标系的标定，李瑞峰等人给出了标准试件标定法、固定基准测试点法及变姿态直接标定法等方法，实现了工具坐标系位置的标定［2］，牛雪娟等人提出三点五步法并采用奇异值分解的方法实现了工具坐标系的位姿标定［3］，Juhaa等人实现了工具坐标系位姿的标定［4］，汤青等人提出了一个通用的工具坐标系标定公式［5］;同时目前商用工业机器人都给出了工程化的工具坐标系标定方法，如Fanuc机器人采用“三点法”及“六点法”实现了工具坐标系位置及位姿的标定。

这些方法的核心思想是采用了一个约束点，增加一个辅助工具，同时需要人工手动示教机器人以不同的姿态使待标定的工具点接近约束点，而且标定精度除了受机器人定位误差的影响外，还受示教精度的影响。本文根据工业机器人定位误差测量系统的特点，采用基于距离约束的方法实现了工具坐标系的自动化标定过程;分步实现了机器人基坐标系的自动化标定过程。同时建立了基于激光跟踪仪的工业机器人定位误差测量系统，并根据测量数据具体标定出了涉及到的各个坐标系，验证了算法的有效性，为工业机器人定位误差测量及补偿打下了基础。涉及到的坐标系的标定过程，无需辅助工具。不仅操作简单，而且还可以排除人为操作因素的影响。

1 工业机器人定位误差测量系统描述

如图1所示，工业机器人定位误差测量系统由测量设备、测量靶标及工业机器人组成。图中P表示待测量的靶标中心，Base为机器人基坐标系，Tool0为机器人法兰盘坐标系，Measure为测量设备坐标系。

在此工业机器人定位误差测量系统中，测量设备可以直接测量出靶标中心P在Measure坐标系下的坐标，同时机器人本身也可以作为测量装置获得被机器人抓着的靶标中心P在机器人Base坐标系下的坐标，两者进行坐标变换便可以统一到同一个坐标系下，进而进行比较获得工业机器人在其工作空间内各个测量点的位置误差。因此工业机器人的定位误差测量系统的测量过程数学模型可表示为

其中:ΔP为工业机器人测量点P的位置误差;PM为测量点P在Measure坐标系下的坐标(由测量设备直接读取);BTM为机器人Base坐标系与Measure坐标系下的转换矩阵(未知量);T0TB为工业机器人Tool0坐标系在机器人Base坐标系下的转换矩阵(可通过机器人示教器直接读取);PT0为P点为Tool0坐标系下的坐标(未知量)。

由此可知，为了获得工业机器人在其工作空间内各个测量点的定位误差，需要对BTM及PT0进行预先标定。

2 测量系统中相关坐标系标定算法

2.1 测量系统中工具坐标系标定

在机器人误差测量系统中，测量靶标中心P在机器人Base坐标系下的坐标可表示为:

其中，N为在机器人工作空间内的测量位置数。任取机器人两个不同测量位置m、n，测量坐标偏差为

同时，靶标中心P在Measure坐标下的坐标偏差为

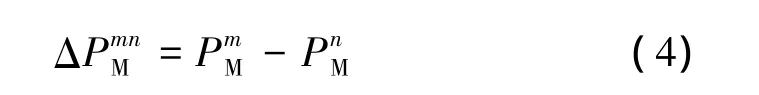
从而有:

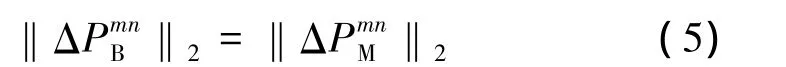
由于T0、T0可以从机器人示教器中直接读取到，、可以由从测量设备中测量获得，通过上式便可以计算出靶标中心P在机器人Tool0坐标系下的坐标，即可标定出靶标中心P在机器人末端的位置，从而可实现工业机器人定位误差测量系统中的工具坐标系的标定。

2.2 测量系统中基坐标系的标定

工业机器人Base坐标系在测量设备Measure坐标系下的转换矩阵可表示为:

众所周知，对于机器人在空间中任意两个不同位置，虽然它们在机器人坐标系和测量坐标系中的坐标值是不同的，但是这两位置在两坐标中的距离长度是相同的［6］，即:

考虑到工业机器人定位误差测量系统的特殊性，可将机器人基坐标系的标定分步进行，即方向向量及位置向量分别标定。

(1)机器人基坐标系的方向向量标定:控制机器人抓着测量靶标，沿自身Base坐标系各个轴运动，并记录测量设备的数据便可得到Base坐标系的各个坐标轴在Measure坐标系下的方向向量，如下:

(2)机器人基坐标系的位置标定:在工业机器人定位误差测量系统中，测量靶标中心的坐标满足以下关系:

式(9)变形可得式(10):

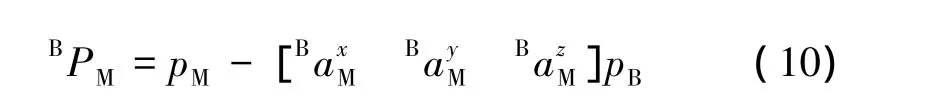
其中，pM可由激光跟踪仪测得;经过测量靶标中心p位置的标定后，pB也可知道。因此通过上式便可计算出Base坐标系原点在Measure坐标系下的坐标值BpM。

机器人基坐标系的X、Y及Z轴在测量设备坐标系的方向向量及原点标定出来后，便实现了测量系统中基坐标系的标定，即有:

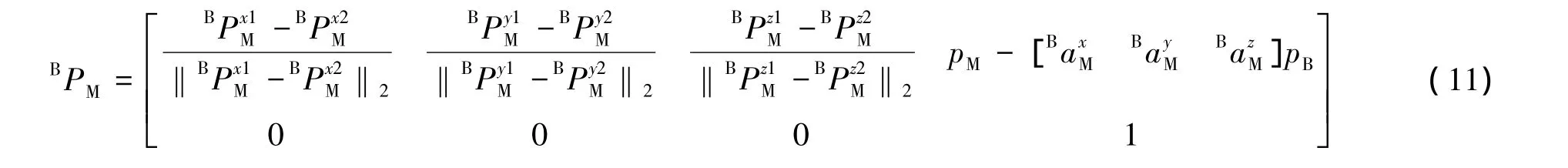
3 实验与标定过程实现

激光跟踪仪作为标定环节中的测量工具，因其具有配置简单，适合应用于工业现场标定场合等优势，越来越受到机器人厂家及研究学者的青睐［7］。因此，在工业机器人定位误差测量系统中的测量设备选择了激光跟踪仪来进行标定研究。

建立的工业机器人定位误差测量系统如图2所示，它包含被标定工业机器人、激光跟踪仪及跟踪靶标。工业机器人采用ABB IRB 4400机器人，此机器人是一种机身紧凑的机器人，承受载荷最高可达60 kg，具有较高的重复定位精度，可广泛应用于切割、去毛刺、清洗、喷涂、研磨、抛光和物料搬运等场合，通过对其绝对定位误差进行标定后，可以大大拓展其应用领域。误差测量设备采用FARO ION型激光跟踪仪，该测量设备具有测量精度高、操作简单等优点，可以直接测得机器人手臂上靶标在其坐标系下的坐标。

3.1 标定数据的采集

由式(6)可知，为了标定出测量靶标工具坐标系，至少需要测量机器人工作空间内的3个点;由式(8)和(9)可知，为了标定出机器人基坐标系在激光跟踪仪坐标系下的坐标，至少需要在机器人每个坐标轴上采集2个点，即总计至少需要采集6个测量点。为了充分表现机器人的特性，对于工具坐标系标定试验过程采集了12个测量点(在机器人工作空间内均匀采集);对于基坐标系标定试验过程采集了30个测量点(每个坐标轴上取了10个点)，数据采集的测量点的分布情况如图3所示。

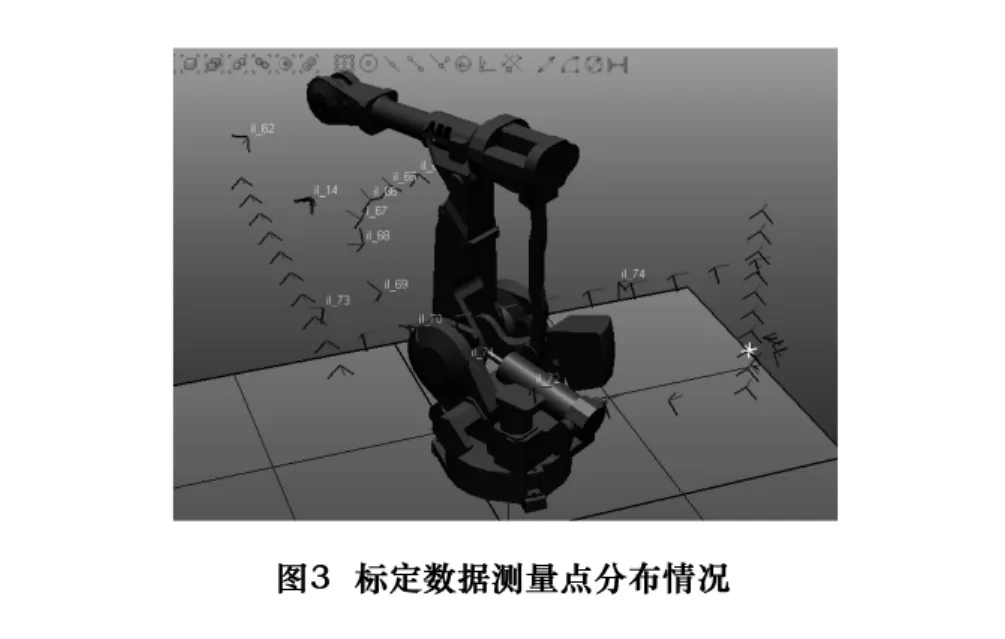
3.2 工具坐标系标定过程实现与分析

虽然采集了12个测量点作为工具坐标系标定的输入数据，但实际标定可选取其中的部分数据使用，这样就可以标定多次，然后对多次标定的结果进行比较分析，可以相互验证标定效果。

根据公式(5)建立的非线性方程为

其中假设每次用来标定工具坐标系的测量点的个数为N。求解工具坐标系时可建立的非线性方程的个数M为

综合式(12)及(13)便可列出M维的非线性方程组，然后通过最小二乘法求解出工具坐标系(x，y，z)。

将采集到的12个测量点数据分成10组分别标定，即首先选择3个不同测量点作为一组，可有4组标定数据来进行标定;然后选择4个不同测量点作为一组，可有3组标定数据来进行标定;接着选择6个不同测量点作为一组，可有2组标定数据来进行标定;最后用12个测量点作为一组来进行标定。从而可标定出10个工具坐标系，标定结果如表1所示。

表1 工具坐标系标定结果

从标定结果看，虽然求解的非线性方程组中只有3个未知数，但由于机器人定位误差的存在，导致非线性方程组的系数误差较大。因此，非线性方程组的维数越小，求解的结果越不稳定;同时，稳定的标定结果也因为采集数据时机器人的位置不同，而标定结果也有微小差别。

3.3 基坐标系标定过程实现与分析

(1)基坐标系方向向量的求解

通过数据采集环节，在机器人每个坐标轴上都选取了10个测量点。根据公式(8)求解基坐标系方向向量的思想，可以转换成根据多个空间点拟合空间直线后，求解直线的方向向量的问题。拟合出的3条直线的方向向量就是机器人基坐标系3个坐标轴在测量设备坐标系下的方向向量。为了简化空间直线的拟合过程，这里可采用分步最小二乘法求解，首先拟合空间直线在XOZ及YOZ平面投影的直线方程，这两条直线方程在O－XYZ中又是两个特殊的平面方程，然后求解两个平面的交线就是我们要求的空间直线［8］。求解出了直线方程，便可以求解出坐标轴的方向向量。根据这种思想拟合出来的一个轴的直线方程为

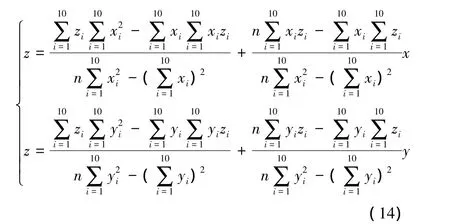
(2)基坐标系位置的求解

求解出来了基坐标系的方向向量后，根据公式(10)便可以由每个测量点计算出一个基坐标系的位置，综合多个测量数据，将多个位置量的均值作为最后基坐标系的位置值，即:

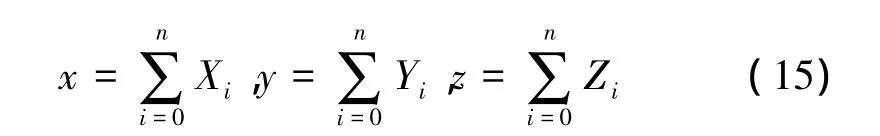
(3)基坐标系标定结果

通过上述公式，根据采集的30组数据，标定出的基坐标系见表2。

表2 基坐标系标定结果 mm

从标定结果看，由于机器人定位误差的存在，导致基坐标系位置标定误差较大。

4 结语

根据工业机器人定位误差测量系统的特点，推导了工业机器人定位误差测量系统中涉及到的工具坐标系及基坐标系的自动化标定公式，建立了基于激光跟踪仪的工业机器人定位误差测量系统，并根据测量数据具体标定出了涉及到的各个坐标系，验证了算法的有效性，为工业机器人定位误差测量及补偿打下了基础。

［1］ROTH Z S，MOORING B W，BAHRAM R.An overview of robot calibration［J］.IEEE Journal of Robotics and Automation，1987，3(5):377－385.

［2］李瑞峰，侯琳琪，陶谦.机器人末端工具参数自动标定方法［J］.哈尔滨工业大学学报，1998，30(3):74－76.

［3］牛雪娟，刘景泰.基于奇异值分解的机器人工具坐标系标定［J］.自动化与仪表，2008(3):1－4.

［4］RONING Juhaa，KORMD Alexander.Method for industrial robot calibrafion［C］//Prceedings － IEEE International on Robotics and Automation.Institute of Electrical and Electronics Engineers，Albuquerque，New Mexico，Apr 20－ 25，1997.3184－ 3190.

［5］GAN Zhongxue，TANG Qing.Visual Sensing and its applications:Integration of laser sensors to industrial robots［M］.Hangzhou:Zhejiang U-niversity Press，2011.

［6］周学才，张启先，郑时雄.一种新的机器人机构距离误差模型及补偿算法［J］.机器人，1991，13(1):44－49.

［7］叶声华，王一，任永杰，等.基于激光跟踪仪的机器人运动学参数标定方法［J］.天津大学学报，2007，40(2):202－205.

［8］霍晓程.空间直线方程的拟合［J］.怀化学院学报，2009，28(2):16－19.