修正的反应谱法地下结构抗震分析初探
2012-09-27宫必宁郑人逢
律 清,宫必宁,郑人逢
(1.河海大学土木与交通学院,江苏南京210098;2.河海大学水利水电工程学院,江苏南京210098)
近年来,有关地下结构的抗震分析方法得到很大发展。地下结构与地面结构的振动特性有着很大的不同,地下结构的振动变形受周围地基土的约束作用显著,结构的动力响应一般较少表现出结构自身的影响[1]。
目前地下结构抗震分析方法有反应位移法、等效水平地震加速度法、等效测力法和时程分析法[2-3]。采用反应位移法计算时,将土层动力反应位移的最大值作为强制位移施加于结构上,然后按静力原理计算内力;时程分析法可以尽可能地描述结构在地震作用下的实际情况,但计算工作量较大[4-5]。振型分解反应谱法计算简便,且方法成熟,但反应谱法是针对地上结构的一种计算方法,有必要对如何利用反应谱法对地下结构进行动力分析作些研究[6]。本文以南水北调工程某倒虹吸为背景,分别用修正的振型分解反应谱法和时程分析法计算,比较两种方法的计算结果。
1 工程概况
倒虹吸全长4 395 m,其中包括进口渠道50 m,南段倒虹吸长1 250 m,中段明渠长2 030 m,北段倒虹吸长1 055m,出口渠道长10 m。虹吸渠段起点设计水位86.785 m,终点设计水位85.591 m,总水头1.194 m,设计流量230 m3/s。南水北调中线一期工程为Ⅰ等工程,该倒虹吸属Ⅰ级建筑物。设计标准按百年一遇洪峰流量8 840 m3/s。倒虹吸结构材料为C40混凝土,倒虹吸土层分布为卵石、卵石浮、粘土、壤土、粉沙、中砂 。
2 有限元模型与计算方法
2.1 有限元分析模型
本文基于ADINA建立倒虹吸平面分析模型(见图1),采用四结点平面单元对模型进行离散,地基中根据材料不同对网格进行分组以采用不同的材料参数进行计算分析。平面模型共有9个单元组,1 920个结点。倒虹吸结构与周围土体建立了接触单元。
2.2 计算分析范围及边界条件
沿倒虹吸结构轴向向北为X正向,垂直于X向指向向西为Y正向,竖直向上为Z正向。计算范围确定的原则是,Y向计算范围从倒虹吸中轴线向两侧各延伸100 m;地基深度从地表向下取42 m深度。
在进行平面分析时,对模型地基两侧以及地基底部截断边界施加法向位移约束,有限元计算按平面应变问题进行。

图1 倒虹吸与地基土平面模型网格图
2.3 计算方法
2.3.1 时程分析法
时程分析法又称逐步积分法,即根据实测的地震加速度记录或人工地震加速度记录直接计算出结构的地震反应过程[7]。时程法可以反应地震随时间变化的全过程,时程分析法全面考虑了地震三要素—加速度峰值、频谱和持续时间对结构的影响,可以尽可能地描述结构在地震作用下的实际情况[8]。
本文采用EL-centro波、天津宁河波以及根据《水工建筑物抗震设计规范》中设计反应谱反演的人工波作为地震输入,计算倒虹吸结构的地震响应。沿坐标轴Y轴,即倒虹吸横断面方向输入地震波,计算时步为1 200步,时间间隔0.01 s。
地震波加速度时程曲线见图2~图4。
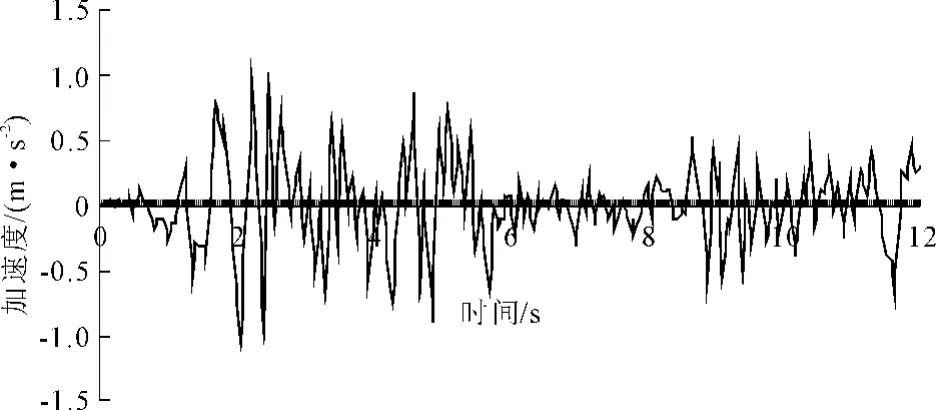
图2 EL-centro波

图3 天津波

图4 人工波
2.3.2 反应谱法
时程法可以反应地震随时间变化的全过程,但计算工作量太大。反应谱法是用于地上单质点体系的地震分析方法,主要反应出结构自身的影响。而地下结构则是处于地基土的包围之中,在地震中,地下结构的振动变形受周围地基土的约束作用显著,结构的动力响应一般较少表现出自身的影响,主要表现地基的自振特性。因此将反应谱法应用于地下结构抗震计算,必须对其修正,在计算结构中考虑结构的自振特性对结果的影响。本文通过计算分析有质量地基与无质量地基条件下结构的振型,选取两种情况下的前几阶振型参与振型叠加反应谱分析,得出倒虹吸结构的地震响应。
设计反应谱取自《水工建筑物抗震设计规范》,反应谱见图5。

图5 设计标准反应谱
图中,β为动力放大系数,即结构的加速度反应与设计地震加速度代表值之比,其值除随结构自振周期和阻尼比变化外,还与结构所在场地类别及震中离场区距离有关,为设计反应谱的最大代表值;T为结构的自振周期;Tg为特征周期,根据场地类别确定。
地震基本烈度为7度,地震动峰值加速度为0.1 g,场地类别为Ⅱ类,Tg=0.3 s,βmax=2.25。
材料参数见表1。

表1 材料参数
3 结果分析
分别对倒虹吸结构的应力与位移进行分析,本文分析的倒虹吸结构位移是相对的位移变形。分别提取时程分析法和反应谱法的最大动应力,最大动位移值,计算最大位移变形。
3.1 时程分析法结果
时程分析法计算结果见表2。

表2 结构最大应力与最大位移变形
3.2 反应谱法结果
反应谱法计算结果见表3。
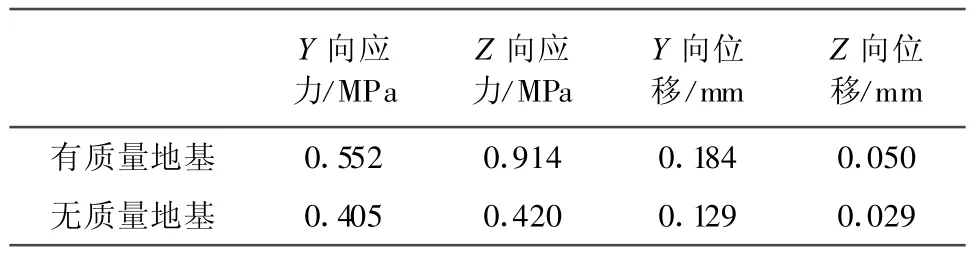
表3 结构最大应力与最大位移变形
由于在反应谱法计算中,一直没有表现出倒虹吸结构的自振性,所以本文尝试将有质量地基与无质量地基振型各取10阶进行计算,结果按一定加权系数进行叠加,有质量地基与无质量地基加权系数分别0.5,0.5;0.6,0.4;0.7,0.3;0.8,0.2,计算结果见表4。

表4 修正的反应谱法结构最大应力与最大位移变形
经比较分析得,当加权系数分别为0.6,0.4时,修正的反应谱法结果与时程分析法结果最为接近,Y向应力与Z向应力的误差分别为2.27%,11.64%;Y向位移与Z向位移的误差分别为8.02%,0。
4 结 语
(1)按本文用修正的反应谱法计算地下结构进行抗震分析,其结果与时程分析法的计算结果误差较小,比较接近,且反应谱法的计算结果要稍大于时程分析法。
(2)反应谱法计算简便,方法成熟,在一定的工程条件下修正的反应谱法可以用于地下结构抗震设计,且偏于安全。
[1]林 皋.地下结构抗震综述[J].世界地震工程,1990,(2):1-2.
[2]张存慧,马震岳,张运良,等.地震荷载作用下水电站厂房结构的震动应力分析[J].水电能源科学,2009,27(5):94-96.
[3]刘建峰.水电站地下厂房动力特性研究及地震反应分析[D].大连:大连理工大学,2007:37-44.
[4]胡志刚.大型水电站地下厂房结构振动计算研究[D].天津:天津大学,2003:61-69.
[5]孙明权,梁成彦,吴小飞.南水北调中线倒虹吸节制闸三向耦合地震响应模拟[J].水电能源科学,2011,29(1):61-63.
[6]郑人逢.倒虹吸结构温度及地震作用影响初探[D].南京:河海大学,2011:61-75.
[7]克拉夫.结构动力学[M].王光远,等译.第二版.北京:高等教育出版社,2006:95-102.
[8]ROY R.Craig,Jr.结构动力学[M].常岭,等译.北京:人民交通出版社,1996:259-278.
