三峡库区某滑坡成灾降雨过程的确定
2012-09-27韩勇
韩 勇
(福建水口发电集团有限公司,福建福州350004)
0 前 言
三峡库区地质灾害防治工程设计的降雨过程是指形成地质灾害的最小降雨过程,也就是成灾降雨过程。降雨引起土体的含水率增大,使边坡土体的基质吸力减小、孔隙水压力增大[1]。含水率增大使土体的抗剪强度减小,导致边坡稳定性降低。本文利用有限元软件Geo-slope计算分析不同降雨与库水骤降条件下三峡库区某滑坡的力学性质,从力学上分析滑坡失稳的概率问题,基于概率统计理论,拟合得到该滑坡成灾降雨过程的概率密度分布函数。本文并不对成灾降雨过程进行讨论,只研究给定降雨过程频率后,如何确定其降雨过程的方法。
1 三峡库区某滑坡概述
某滑坡位于长江西陵峡与巫峡之间,湖北省巴东县城下游1.5 km的长江北岸,下距三峡坝址66 km,是黄蜡石滑坡群的重要组成部分。滑坡位于黄腊石滑坡群的中前部,该滑坡在平面上近似呈梯形分布,高程位于60 m~350 m之间,滑坡方量为700×104m3~800×104m3。滑体物质成分主要为浅绿色泥灰岩和紫红色泥岩,滑坡体结构为散裂及碎裂结构,地质纵剖面如图1所示。滑坡属复活性蠕滑期渐进推移式水库、降雨型深层岩质切层类滑坡,滑坡体在三峡水库蓄水前处于自然状态,在水库蓄水后出现过较大的变形。

图1 滑坡地质纵剖面
2 降雨过程的随机变量及概率分析
2.1 成灾降雨过程概率的一般表达[2]
成灾概率一般可以表达为:

式中:fR.L(r.l)为抗力(R)和降雨引起的推力(L)的联合概率密度函数(这个为文章的关键地方)。若降雨引起的推力(L)和抗力(R)是随机独立的,则:

则(1)可写成:

如果我们认为抗力R是变量,那么当L大于rD时;
FR(l)=1 L为其它值时: FR(l)=0则成灾降雨过程的概率一般式为:

2.2 威布尔(Weibull)三参数概率分布表达式[3]
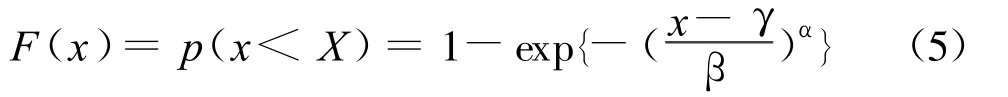
以类似概率矩的形式定义可靠性矩,利用子样矩样估计母体矩从而获得参数估计的一种方法,对威布尔分布,采用一阶、二阶和四阶矩可以得到参数估计的表达式,即

2.3 稳定性计算方法
本文在进行稳定性分析计算时选用的方法理论为极限平衡法中同时考虑力和力矩平衡的较完备的摩根斯坦-普莱斯法[4]。
3 研究方法
(1)通过收集该滑坡地质资料和近20 a的降雨资料,分析滑坡的地质结构和地层岩性特征。
(2)通过对该滑坡地形地貌、地质构造、地层岩性和水文地质条件的分析,建立起该滑坡地质模型;
(3)采用均匀设计方法,基于滑坡所在区域的降雨资料,对可能成灾的降雨强度、降雨历时和水库水位骤降速度等影响该滑坡稳定性的关键因素进行组合设计[5],为研究该滑坡的推力和抗力分布规律提供合理的计算工况;
(4)采用数值模拟方法,计算滑坡在(3)所涉及的计算工况条件下滑坡的推力和抗力大小并获得其规律;
(5)在(4)的基础上,采用概论统计方法,通过严谨的数学分析,获得该滑坡在降雨条件下的推力和滑坡岩土体本身抗力之间的联合概率分布函数表达;
(6)在(5)的基础上,通过建立适合该滑坡的成灾降雨过程的概率表达式,并形成该滑坡成灾降雨过程的确定方法[6]。
4 数值计算模型
4.1 网格模型
对图1的主纵剖面采用四边形单元进行有限元网格的剖分,节点数为17 769个,单元数为17 991个,网格图见图2。

图2 滑坡有限元计算网格图
4.2 边界条件
滑坡在降雨和水库水位变化条件下渗流的边界条件描述如下:
(1)水头边界:该斜坡前缘被库水浸没部分为水头边界。
(2)流量入渗边界:斜坡表面处取降雨引起入渗的流量边界,当降雨强度大于坡面岩土体的入渗速度时,取岩土体的入渗速度值作为边界流量值;当降雨强度小于坡面岩土体的入渗速度时,取降雨强度值作为边界流量值[7]。
(3)两侧和底部渗流边界:模型底面和两侧为自由渗流边界,此基岩的渗透性很小,可认为是不透水边界[8]。
各边界条件的表达见图3。
5 计算参数
根据该滑坡地质勘查报告及该滑坡的前期研究成果,其滑体及滑带的土~水特征曲线及渗透函数曲线见图4和图5,其它物理力学参数见表1。

图3 滑坡在各种边界条件下渗流示意图

图4 滑体土~水特征曲线及渗透函数曲线
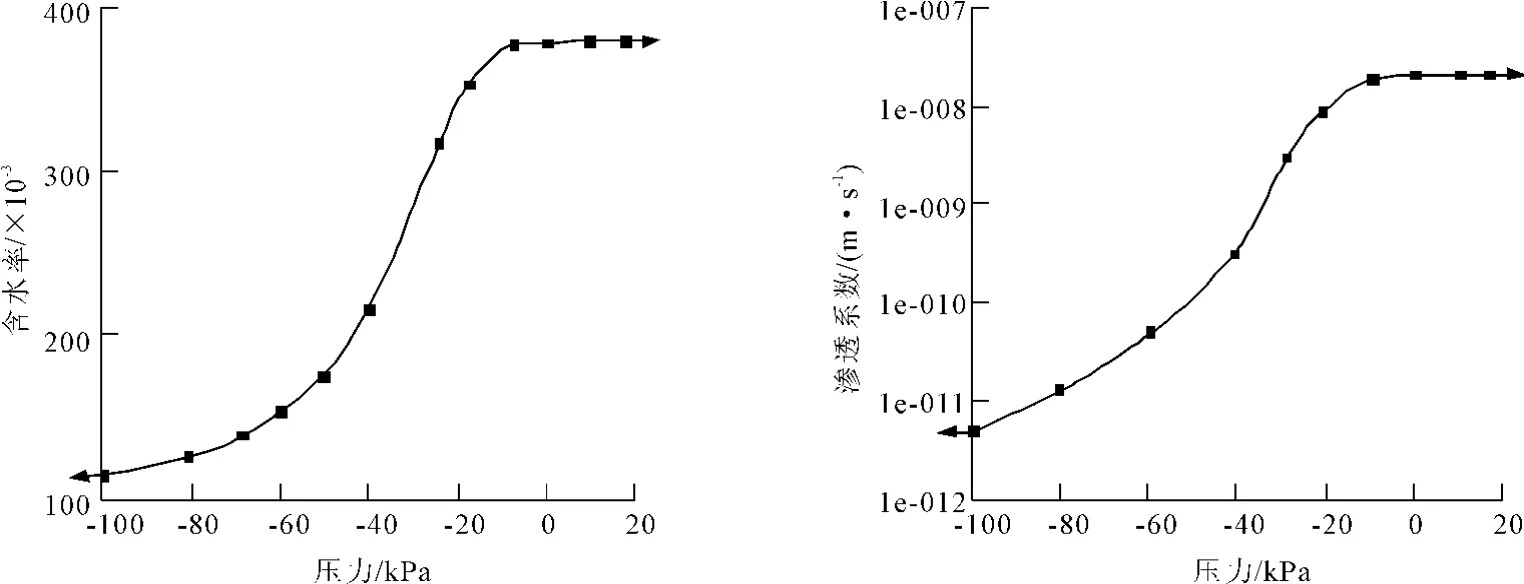
图5 滑带土~水特征曲线及渗透函数曲线

表1 岩土体物理力学参数
6 计算方案
从三峡水库调度和该滑坡所在区域20 a(1984年~2003年)月平均降雨量分布图(图6)来看,在每年4月底到6月中旬是三峡水库从正常蓄水位175 m消落到145 m的时段,同时也是该滑坡所在区域降雨相对很集中的时段(降雨强度和总量都较大,见图7),因此选择对该滑坡稳定性相对最不利的水库水位骤降和降雨强度及降雨总量相对较大的工况进行该滑坡成灾降雨过程推求。
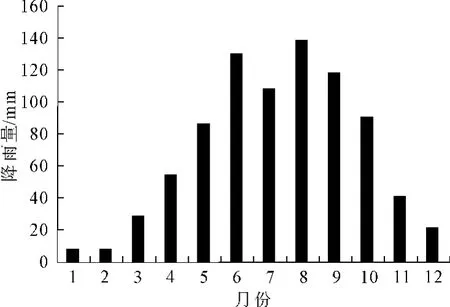
图6 滑坡所在区域月平均降雨量分布图
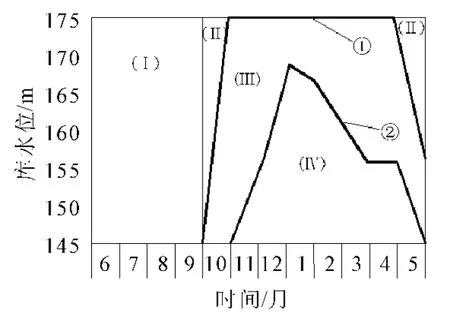
图7 三峡工程正常蓄水位175 m时水库调度图
采用均匀设计方法,对影响该滑坡稳定性的3个主要影响因素[9]:降雨历时、库水骤降速度和降雨强度进行计算方案的设计,为该滑坡在库水位变化和降雨条件下推力和抗力联合概率密度的确定提供样本。对滑坡稳定性影响的各主要因素的取值水平见表2。采用U45(53)均匀设计给出45种试验组合方案,具体方案见表3;采用饱和非饱和非恒定渗流理论计算滑坡在各方案条件下的地下水位(见图8)和孔隙水压力的变化[10],以此为基础,采用极限平衡方法中的摩根斯坦-普莱斯方法计算滑坡在各工况条件下的推力和抗力[11],计算结果见表3。
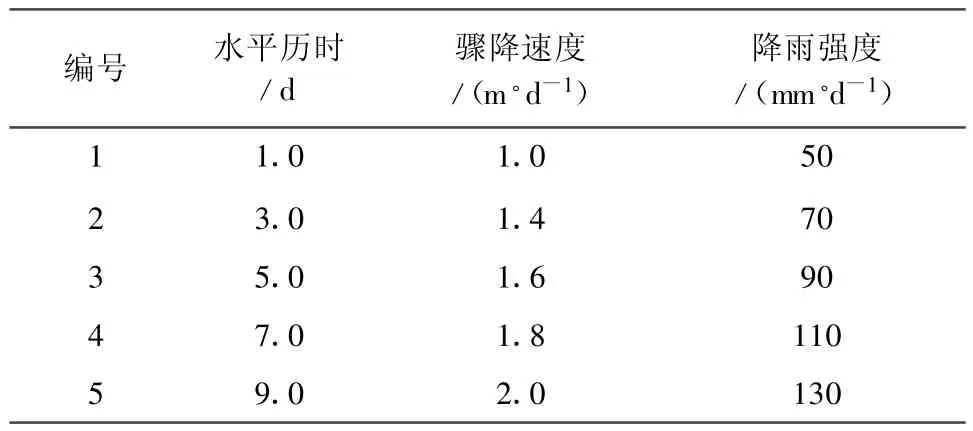
表2 影响滑坡稳定性的主要因素取值水平
7 推力和抗力联合概率密度函数的推求
根据表3的计算结果,采用Easyfit软件进行概率分布函数的拟合,可以获得该滑坡在降雨和库水位骤降条件下滑坡推力和抗力的联合概率密度函数为[12]:
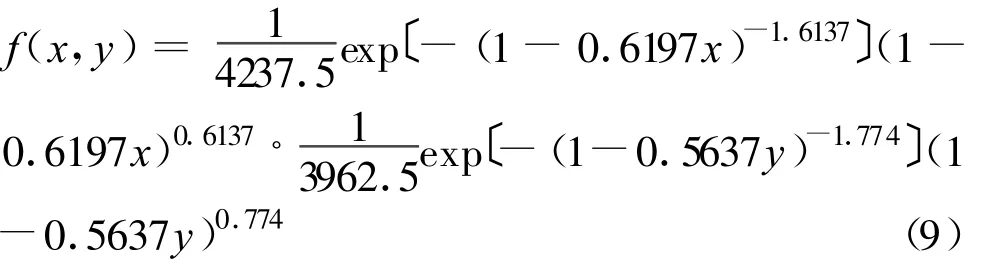
式中:x为滑坡的推力(kN);y为滑坡的抗力(kN)。

图8 滑坡地下水位变化过程图

表3 U45(53)均匀设计组合方案
由上述推力和抗力的概率密度分布形式属于广义极值分布函数,形状参数k(-0.6197、-0.5637)均小于零,符合广义极值 Щ分布,即威布尔(Weibull)分布。
由于不同的降雨强度、不同的降雨工况下计算所得到的推力与抗力的数值都存在一一对应的关系[13],因此,我们可以认为降雨强度及降雨历时的分布也同样符合威布尔(Weibull)分布。
8 实例分析
该滑坡区的年最大降雨资料如表4和表5。

表4 年最大降雨量

表5 年最大降雨量历时天数
根据实测降雨资料计算所得威布尔各参数值见表6。

表6 计算参数表
通过对降雨资料的整理分析可以得到如下公式。
降雨历时的概率分布公式:
降雨强度的概率分布公式:

联合概率公式:

当降雨历时为t=5 d,重现期为五十年一遇Pf=0.02,求得降雨强度为¯i=45.73 mm/d。
9 结 语
从力学性质的角度分析滑坡失稳的概率,打破了以往仅通过研究降雨与滑坡之间的概率统计关系来预测滑坡失稳的概率。
以三峡库区某滑坡为例,整理分析该地区的降雨实测资料,得到该滑坡成灾降雨过程的降雨历时、降雨量的联合概率密度分布形式。利用公式计算当降雨历时为5 d,重现期为五十年一遇的降雨强度为¯i=45.73 mm/d,为三峡水库蓄水后重大水库复活型滑坡预报模型和预报判据的建立提供合理的计算依据。
[1]顾慰慈.渗流计算原理及应用[M].北京:中国建材工业出版社,2000.
[2]童广勤,郭其达,谭宏.三峡地质灾害防治工程设计降雨过程统计分析[J].人民长江,2007,38(11):86-87.
[3]段忠东,周道成.极值概率分布参数估计方法的比较研究[J].哈尔滨工程大学学报,2004,36(12):1606-1609.
[4]钱家欢,殷宗泽.土工原理与计算[M].北京:中国水利水电出版社,1996:320-324.
[5]张学年.长江三峡工程库区顺层岸坡研究[M].北京:地震出版社,1993.
[6]华东水电学院.西北农学院.武汉水利电力学院.水文及水利水电规划[M].北京:水利出版社,1979.
[7]王飞,王媛,倪小东.渗流场随机性的随机有限元分析[J].岩土力学,2009,30(11):3539-3542.
[8]束龙仓,李伟.北塘水库库底地层渗透系数的随机特性分析[J].吉林大学学报(地球科学版),2007,37(2):216-220.
[9]高江平,李 芳.黄土邓肯-张模型有限元计算参数的试验[J].长安大学学报(自然科学版),2006,26(2):10-21.
[10]毛昶熙.渗流计算分析与控制[M].北京:水利电力出版社,1991.
[11]浙江大学数学系高等数学教研组编.概率论与数理统计[M].北京:人民教育出版社,1979.
[12]张有天,王镭,陈平.边界元方法及其在工程中的应用[M].北京:水利电力出版社,1989.
[13]施小清,吴吉春,袁永生.渗透系数空间变异性研究[J].水科学进展,2005,16(2):210-215.
