协整理论在企业所得税分析与预测上的应用——以深圳市金融业为例

丛 静

（深圳市国家税务局 海洋石油税收管理分局，广东 深圳 518000）

协整理论在企业所得税分析与预测上的应用
——以深圳市金融业为例

丛 静

（深圳市国家税务局 海洋石油税收管理分局，广东 深圳 518000）

运用协整分析和因果检验的方法，建立了金融企业所得税收入与宏观经济指标的数理统计模型，希望运用此模型能够达到深化税收分析与预测工作，加强税源监控，提高征管质效的目的。

协整理论；企业所得税；深圳市；金融业

国内已有的关于税收的研究成果多数是关于税收整体收入与经济增长关系的探讨，很少关于具体行业、税种与相关经济变量关系的研究［1］。本文以深圳市金融企业所得税为例，遵循从经济到税收的原则，以经济为参照，综合运用协整分析和因果检验的方法，建立金融企业所得税收入与宏观经济指标的数理统计模型，深入剖析宏观经济对税收的影响，从而达到深化税收分析与预测，加强税源监控，提高征管质效的目的。

一、变量筛选及数据处理

根据企业所得税法规定，企业所得税实行季度预缴、年度汇算清缴的征收方式。企业所得税预缴部分依赖于企业的当期利润，与宏观经济的形式密切相关。而汇算清缴时的纳税调整部分涉及到税前扣除项目限额、税收优惠政策等多项税收政策，受税收政策影响较大，而与经济指标的相关性不高。因此，在进行企业所得税收入与经济相关分析时，只考虑企业所得税预缴因素，而将年度汇算清缴作为特殊因素加以剔除。新企业所得税法实施前，深圳地区施行15%和33%的两档税率；新法实施后，深圳地区在5年内实行过渡期税收优惠政策，税率逐年提高。为避免税率调整对税收带来的影响，需要剔除税率这一因素，因此选取企业所得税预缴的应纳税所得额作为因变量来分析经济因素对其的影响。本文以2007—2009年深圳金融业企业所得税季度预缴税款和2007—2009年相关经济指标的季度数据作为分析所用数据（见图1，数据来源于深圳市国家税务局CTAIS数据查询系统）。

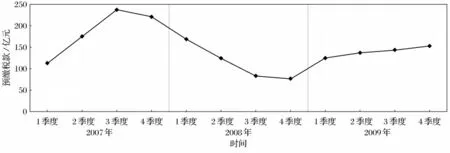
图1 2007—2009年深圳市金融业季度应纳税所得额预缴趋势图

在影响金融企业应纳税所得额的众多相关经济指标中，选取比较有代表性的深圳市金融业GDP、沪深两市成交额、货币供应量M1、深圳市金融机构存款增量、深圳市金融机构贷款增量5项指标［2］。通过Eviews软件计算分析，只有沪深两市成交额与应纳税所得额的相关度较高，两者之间的相关系数为0．78。为了更深入地分析深圳金融企业所得税预缴收入与沪深两市成交额的关系，本文运用计量经济学中的协整检验方法对两者的相关性进行检验。

二、实证分析

深圳市金融业企业所得税应纳税所得额（INC）与沪深两市成交额（VOL）之间的关系，主要从以下3个方面分析：应纳税所得额与两市成交额之间是否存在协整关系；用Granger因果关系检验法检验INC和VOL的因果关系；应用误差修正模型进行预测。

1．协整检验

时间序列建模分析中，一般要求所用的时序必须是平稳的，即没有随机趋势或确定性趋势，否则将会产生“伪回归”问题，即变量之间本来没有相互依存关系，而回归结果却显示出它们之间存在这种关系的错误结论。在实证分析中，数据通常都是非平稳的，为了避免产生“伪回归”，检验时间序列变量之间是否存在长期的稳定关系。本文采用EG两步法对应纳税所得额与沪深两市成交额之间的关系进行协整检验。

为了防止数据剧烈波动及异方差问题，对数据进行对数处理：

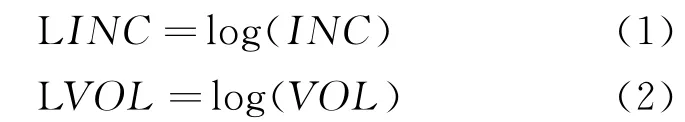
（1）平稳性检验。采用Eviews软件对LINC和LVOL序列进行平稳性检验，具体采用ADF检验法。ADF检验方法通过在回归方程右边加入因变量的滞后差分项来控制高阶序列相关，主要通过下述3个自回归模型来实现ADF检验：

模型（3）用于没有明显趋势和截距的变量序列检验，模型（4）用于有截距而没有趋势的变量序列检验，模型（5）用于对有趋势和截距的变量序列进行检验。

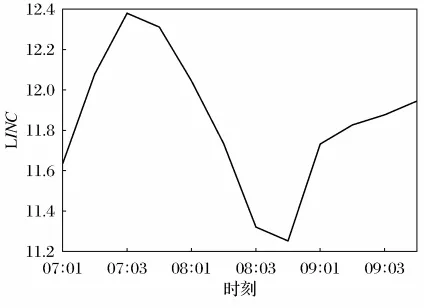
图2 LINC的时序图

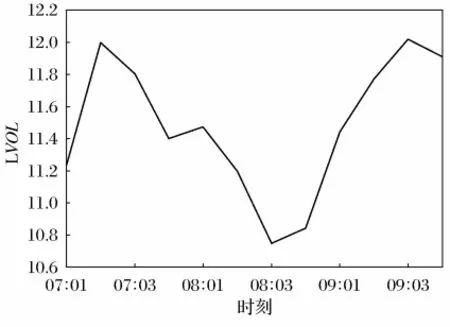
图3 LVOL的时序图

从图2和图3中可以看出，LINC和LVOL序列具有大致相同的增长和变化趋势，故在使用ADF检验时选用模型（4）进行平稳性检验。结果见表1。

表1 LINC和LVOL的单位根检验结果

检验结果均显示，LINC和LVOL的ADF的检验T统计量大于其相应的1%、5%、10%显著性水平临界值，因而接受原假设，即两个变量均是非平稳序列。

（2）单整性检验。用Eviews对LINC和LVOL序列的差分进行平稳性检验。检验结果见表2。

结果显示，LINC一阶差分的ADF检验T统计量小于相应的5%显著水平临界值，LVOL一阶差分的ADF检验T统计量小于相应的10%显著水平临界值，因而LINC和LVOL的一阶差分在10%显著性水平上为平稳序列；即LINC和LVOL为一阶单整，有LINC～I（1），LVOL～I（2）。

表2 LINC和LVOL的单整性检验结果

以上检验结果表明，LINC和LVOL均为一阶单整序列，满足协整回归条件，可以对其进行协整检验。

（3）协整关系检验。检验因变量和解释变量之间是否存在协整关系采用的办法是利用因变量对自变量进行最小二乘回归，再对模型估计残差序列作单位根检验，看其是否是一个平稳序列，见表3。

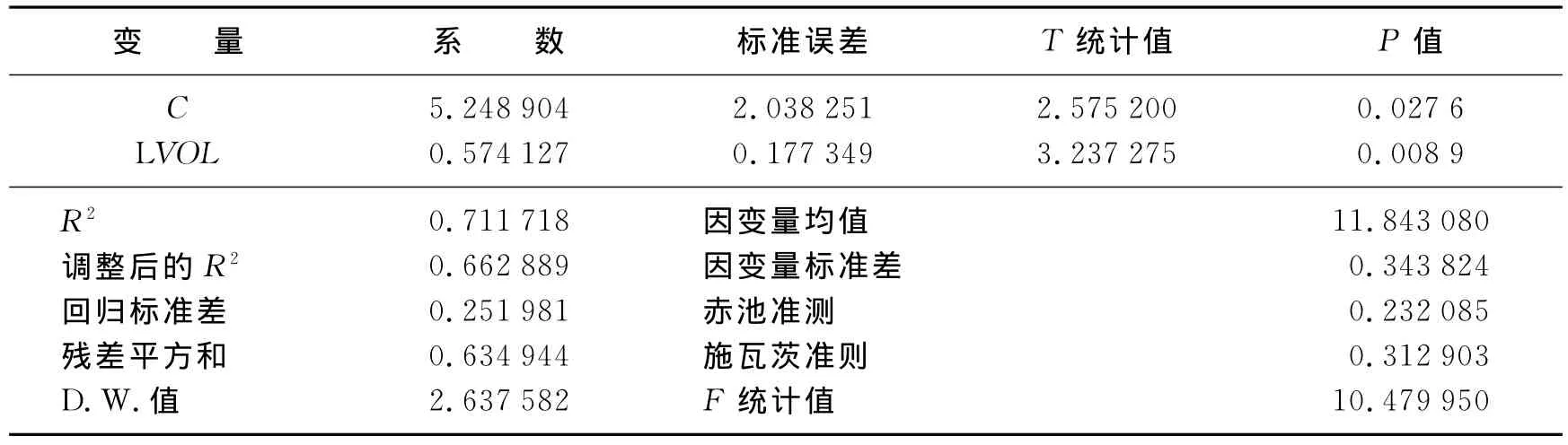
表3 回归方程及相关检验结果

第一，建立回归模型

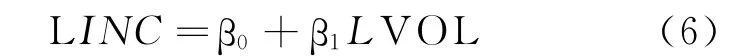
用最小二乘法进行回归，得到

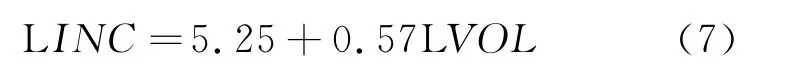
第二，利用Eviews软件对式（7）残差序列进行平稳检验，采用模型：

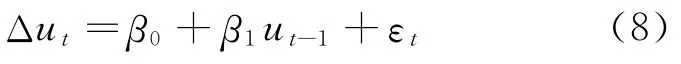
检验结果见表4。由于检验统计量值－4．458 359小于5%显著性水平的临界值－3．423 9，因此估计残差序列e为平稳系列，序列LINC与LVOL具有协整关系。

表4 序列e的ADF检验结果

由协整方程可知，深圳市金融业的企业所得税季度应纳税所得额与两市成交额之间存在着长期的均衡关系，系数0．574 1表示两市成交额每增长1%，企业所得税季度应纳税所得额就平均上升0．574 1%。由于季度应纳税所得额乘以税率等于季度预缴企业所得税税款，因此协整方程的弹性系数说明了深圳市金融业企业所得税季度税收与两市成交额的正相关关系。经典的回归模型由于没有考虑到经济时间序列的不平稳性，从而容易导致计量经济模型出现偏差，而通过误差修正模型可以对这些偏差进行修正，因此误差修正模型比经典回归模型更能反映经济变量之间存在的长期均衡关系。

2．误差修正模型

通过上述分析可知，LINC与LVOL为一阶单整序列，两者之间为协整关系。根据协整方程（7）得到残差序列e，令误差修正项ECMt＝e，建立误差修正模型［3］

进行回归后，得到误差修正模型

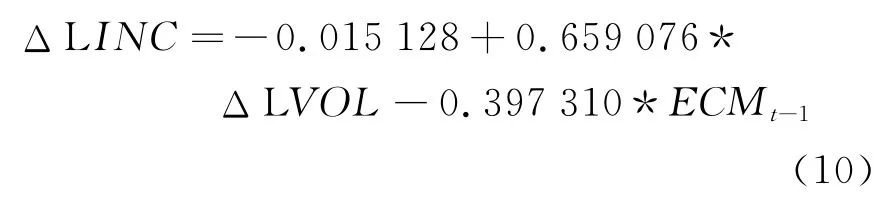
相关检验结果见表5。

表5 ECM估计及相关检验结果

在上面的误差修正模型中，差分项反映了短期波动的影响。应纳税所得额LINC的短期变动可以分为两部分：一部分是两市成交额波动的影响；一部分是偏离长期均衡的影响。误差修正项ECMt－1的系数大小反映了对偏离长期均衡的调整力度。从系数估计值（－0．397 3）来看，当短期波动偏离长期均衡1%时，以－0．397 3%的调整力度将非均衡状态拉回到均衡状态。

上面误差修正模型的拟合度达0．63，说明该模型较好地反映了深圳市金融业应纳税所得额与两市成交额的关系。该模型也说明了深圳市金融业应纳税所得额与两市成交额之间存在正相关关系。当两市成交额上升或者下降1%时，深圳市金融业应纳税所得额就会上升或下降0．659 1%。

3．因果关系检验［4］

协整检验的结果说明应纳税所得额与沪深两市成交额之间存在一个长期的均衡关系，不过并未给出二者的因果关系，这就需要进一步进行格兰杰因果关系检验。由于格兰杰因果关系检验的前提是变量序列平稳或存在协整关系，因此可以对已经证明具有协整关系的LINCt和LVOLt进行格兰杰因果关系检验。根据AIC准则确定最优滞后阶数为3，运用Eviews得到检验结果见表6。

表6 格兰杰因果检验结果

从检验结果可以看出，在5%显著性水平下，LVOL是LINC的格兰杰成因，即沪深两市成交额是应纳税所得额的决定因素。

4．模型预测

利用上述建立的深圳金融行业企业所得税应纳税所得额与两市成交额的误差修正模型进行2010年第1季度应纳税所得额预测。

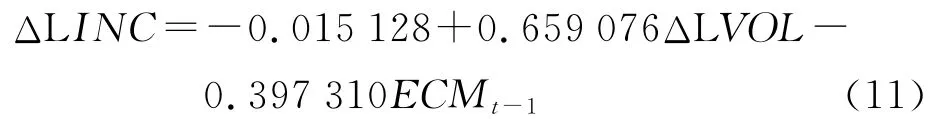
解释变量两市成交额2010年第1季度为116 334亿元，通过下式计算出另一解释变量ECM（－1）＝－0．146 756 57。

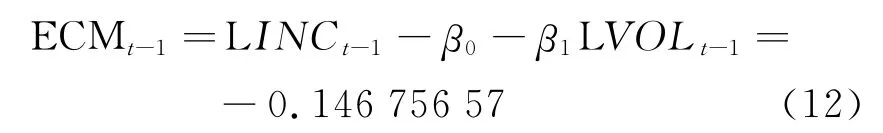
利用误差修正模型进行预测得到ΔLINC为0．087 378 691。可知，2010年第1季度深圳市金融行业企业所得税应纳税所得额为1 675 723万元，按照22%的税率换算成预缴企业所得税税额为368 659万元，与实际值（350 102万元）的误差率为5．3%，预测结果比较理想。

三、结果与讨论

通过对深圳市金融企业所得税应纳税所得额与沪深两市成交额的协整分析，得出以下结论：深圳市金融企业所得税预缴的应纳税所得额与沪深两市成交额之间存在长期均衡的关系，沪深两市成交额是应纳税所得额的格兰杰成因，可以利用两者的相关关系对企业所得税的季度预缴收入进行预测。在企业所得税收入年度预测时，还需考虑汇算清缴、代扣代缴以及稽查补税等因素，该部分收入受政策影响较强，在实际工作中还需根据现实情况对模型计算出的结果进行调整［5］。从深圳金融企业所得税收入的实际情况看，其预缴企业所得税收入占全部所得税收入的80%以上，因此本文建立的模型在很大程度上解释了税收变化情况，对基层税收分析与预测工作具有很强的指导作用。

［1］付广军．中国税收统计与计量分析［M］．北京：中国市场出版社，2005：11．

［2］焦瑞进．宏观税收分析指标体系与方法［M］．北京：中国财政经济出版社，2007：235－237．

［3］易丹辉．数据分析与Eviews应用［M］．北京：中国统计出版社，2002：153－155．

［4］张雪莹，金德环．金融计量学教程［M］．上海：上海财经大学出版社，2007：220－221．

［5］张伦俊．税收与经济增长关系的数量分析［M］．北京：中国经济出版社，2006：279－280．

【责任编辑：刘晓鸥】

Application of Cointegration Theory in Analysis and Forecasting of Enterprise Income Tax——Taking Financial Enterprises in Shenzhen for Example

CONG Jing
（Offshore Oil Tax Administration Branch，Shenzhen State Administration of Taxation，Shenzhen 518000，China）

Using cointegration analysis and causality test method，the mathematical statistical model of financial industry enterprise income tax and the macroeconomic indicators is established，in order to deepen the analysis and forecasting of tax revenues，strengthen the monitoring of tax sources and improve the quality of collection efficiency．

cointegration theory；enterprise income tax；Shenzhen；financial industry

F 22

A

1008－3862（2012）04－0025－05

2011－12－01

丛 静（1982－），女（满族），辽宁沈阳人，深圳市国家税务局，经济师。