一种动态水流生成新方法

齐 敏，周加军，李大健，崔赫琳

（1.西北工业大学 陕西 西安 710129；2.西北工业大学365研究所 陕西 西安 710129）

在虚拟现实和可视化仿真中，对自然景物的模拟是其研究的重点之一。动态水流经常出现在虚拟环境当中，它能够在很大程度上增加虚拟环境的真实感。水流与烟雾、火焰一样，其形状和运动的方式受其它景物的影响，没有规律性，因此不能用传统的几何建模方法来创建它。

目前有多种形成水波的方法，在国外，Peachey[1]采用了正弦函数与二次函数线性组合的方法来模拟波浪外形。Fournier[2]等人则利用构造参数曲面合成的方法来模拟比较复杂的海浪。Foster[3]等人使用有限差分近似求解Navier-Stokes方程，用得到流速场和压力场产生水波高度场模拟出较真实的水面效果。Perlin[4]提出了一种噪声图像合成方法，利用噪声函数生成连续的二维噪声曲面，再叠加成分形曲面。Johanson[5]利用Perlin噪声和投影网格来模拟海浪等。

在国内，杨怀平和孙家广[6]从海洋学观测的经验入手，利用海浪谱对深水波进行了模拟。李广鑫[7]等人引入Perlin噪声作为水面高度场动态变化的激励源，使用准均匀B样条曲面来构造水面，来模拟水面连续动荡变化的效果，而且用CubeMap纹理映射技术模拟了水面的反射效果等。宋利等人利用Fourier[8]合成技术，对模型表面利用静止水面的图像数据进行纹理映射，模拟雨滴下落的自然现象。

1 Perlin噪声

Perlin[4]噪声是由Ken Perlin发明的自然噪声生成算法。可以用来模拟自然界中的噪声现象。用它可以得到连续变化的二维图像，例如可以用它来模拟人体的随机运动，蚂蚁行进的线路，也可以通过计算分形和模拟云朵、火焰等非常复杂的纹理。Perlin噪声对各个点的计算是相互独立的，非常适合使用图形处理器进行计算。

创建Perlin噪声函数，需要有一个噪声函数和一个插值函数：

1）噪声函数基本上是一个种子随机发生器。它需要有一个整数作为参数，然后根据这个参数得到一个随机数。对于相同的两个参数，会得到相同的结果。

2）可以在两值之间进行平滑插值，来形成一个可以输入非整参数的连续函数，由此来填充两个随机点之间的非整数的空白部分，目前常用的插值函数有线性插值、余弦插值、立方插值以及多次方插值函数。本文中Perlin利用余弦插值进行平滑，得到了很好的平滑效果。

在文中需要利用二维的Perlin噪声函数对水面纹理进行扰动。首先要构造一个二维梯度场，如图1，将二维噪声面分割为个网格，每个网格点则为噪声面的控制点，每个控制点的梯度方向和长度都是随机产生的，并且是一次性的，但是在求每个噪声控制点的过程中，其梯度是不变的，这就使得Perlin噪声对于相同的整数输入，产生相同的输出。

图1 噪声网格梯度图Fig.1 Gradient map of noise grid

设噪声函数为 PerlinNiose（x，y），I（x，y）为任意一点的噪声值，如果I（x，y）的坐标为整数，则其数值等于原始的数值，如果I（x，y）的坐标不为整数坐标，其数值则由包围它的单位四边形上的四个点来插值求得。其相邻的四个控制点为N（i，y），N（i，j+1），N（i+1，j），N（i+1，j+1），其中 v（i，j）v（i，j+1），v（i+1，j），v（i+1，j+1）分别为这 4 个点的梯度，这 4 个控制点对待插点的的贡献值为：

然后在 x，y 方向上利用 D1，D2，D3，D4对 I（x，y）进行余弦插值，即可得到平滑的噪声平面。其余弦插值函数为

2 OpenGL着色语言

可编程的图形硬件是提高图形程序设计灵活性和效率的一个重要手段，随着图形处理单元GPU的逐渐完善，OpenGL着色语言（GLSL）应运而生，它可以使得开发人员可以很好的控制图形处理管线，实现各种完美的图形渲染效果。

最新的GLSL主要包含顶点着色器（Vertex Shader），片元着色器（Fragment Shader），和几何着色器（Geometry Shader）。

1）顶点着色器 在OpenGL着色语言中，顶点不仅是位置坐标值，还包括法线坐标、纹理坐标、颜色坐标、雾坐标和自定义属性坐标。在顶点处理的过程中，数据通过attribute变量，uniform变量和纹理贴图的方式传递给顶点着色器。经过处理后的数据再通过varying变量和专用的顶点着色器输出变量从顶点着色器输出，并将顶点插值得到的结果传入几何着色器，或者片元着色器。

2）片元着色器 是一个可编程的处理面片数值及数据的单元。片元处理器可以完成对图形的插值，纹理的访问等相关处理，以及实现雾化效果和颜色求和。片元着色器可以处理光栅化生成的点、线、多边形，像素集合及位图等，但面片处理器不能完成多个面片的同时操作。

3）几何着色器 几何着色器的操作对象是图元，包括一维的点图元，二维的线图元，三维的三角形图元。几何着色器利用内置变量gl_VerticesIn获取当前的图元的维数，从而获得图元的每个元素的数值。并且几何着色器要求用户主动设置输入和输出图元的性质。

OpenGL着色器在渲染管线中的位置和作用如图2所示。

图2 OpenGL着色器渲染流程Fig.2 Flowing chart of OpenGL Shader

顶点着色器可以完成顶点替代、法线变换、生成和变换纹理坐标、光照及材质应用的功能；片元着色器则可以实现替代纹理、雾化、像素汇总的功能；几何着色器在图元装配的过程中生成新的图元。

3 动态水面

文中利用Perlin噪声作为驱动源，扰动输入的水面图片，再通过OpenGL渲染语言进行图片中片元法线、颜色操作等，便可形成比较真实的水面。

首先创建一个几何平面，然后把将要当做水面纹理的纯色图片映射到几何平面上，作为动态水面的初始高度场。采用此种方法，可以把三维立体波浪的求解过程变换为对二维平面扰动来求解波浪面。从而较求解传统波动方程，可以大大简化计算过程和减少工作量。

在文中，高度场是由Perlin噪声扰动纹理数据来形成的，纹理上的相应点的高度值是随着噪声控制点的变化趋势而变化的。其波动方程可表示为：

其中x，y为水面相应点的横坐标与纵坐标，t代表当前时刻，则 Z（t）表示在噪声的扰动下，坐标（x，y）处点的高度值。当Z（t）=0 时，表示该点处于水平面状态，当 Z（t）不等于 0 时，则表示该点处于已形成的水波面上。对于该水面，以一定的间距把水面分割为有点的网格面，本文中以1为单位，使得相邻的网格点组成单位矩形面，在网格点上，根据公式1即可求得其对应坐标的数值，不在网格点上的点数值则由相邻的点插值得到。其插值过程如下。

3.1 待插点周围网格点的平滑

对于任意一点的I（x，y），由包围它的四个点进行插值，这四个点分别为 N（[x]，[y]），N（[x]+1，[y]），N（[x]，[y]+1），N（[x]+1，[y]+1），为了得到平滑的效果，在插值之前，先对这四个点进行平滑。平滑按照Perlin噪声的平滑公式进行平滑，以N（[x]，[y]）点为例，得到的结果为：

用同样的方法可以求得其他 3 个点 N（[x]+1，[y]），N（[x]，[y]+1），N（[x]+1，[y]+1）的数值，然后利用得到的平滑后的点，分别在X，Y方向上进行余弦插值。

3.2 余弦插值

余弦插值公式为：

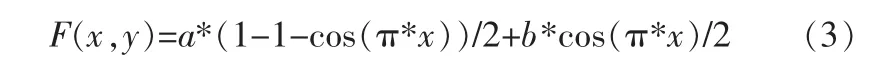
其中a，b代表根据公式2求得的各个网格点的平滑结果，x代表网格点与相应点在X方向的距离，即可看做在插值中，各网格点对待插值点的贡献值。

设在 X 方向的插值结果分别为 F1（x，y），F2（x，y）。

利用这两个结果再在Y方向上进行插值，即得到I（x，y）处的数值。

其中y代表待插点与相应点在Y方向的距离。经过此项插值可获得平滑的水面高度场，此时可得到平滑动荡的水面，此时的水面还没有具备水面的特性，既没有反射、映射等效果。接下来通过水面法线等计算来实现以上效果。

3.3 法线的计算

文中法线的计算是以网格中单位矩形为单位面片的。

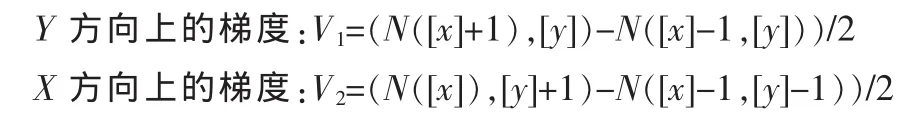
所以该单元面的法线为：

随着水面的波动，各个单元面的法向量也随着变化，由于各个单元面的法向量不同，所以就出现了明暗不同的效果。再通过OpenGL渲染语言对生成的水面进行渲染，对法线进行实时更新，实时计算各个面的法线，同时根据网格中每个点的高度来调节点的颜色值，使得不同高度的点呈现出不同的颜色值，从而实现接近真实水面的色调。

3.4 实时镜面反射

本文中的反射效果根据OSG中的模板缓存[9]来实现的。根据镜面反射[10]原理，在绘制虚拟环境实体时，还要对它施加矩阵变换来实现关于镜面的对称影像。然后将镜面影像写入模版缓存，以防止超出镜面范围的镜像被显示。然后根据反射原理求得观察景物倒影视线与水面的范围，将景物倒影进行投影变换，映射到水面的可视范围，从而对影像与水面混合绘制。随着视点位置的变化，对倒影的可视区域位置也会发生变化，在此重新对倒影进行投影变换，从而获得真实水面影像。

图3 反射原理Fig.3 Principle of reflection

图4 动态水面效果图Fig.4 Flowing warter surface

4 结 论

对动态水面的模拟始终是虚拟现实领域研究的重点之一，本文利用Perlin噪声扰动水面纹理形成水面高度场，同时在 OSG基础上利用OpenGL Shader渲染语言进行水面渲染，并且实现实时的水面映射效果的方法，具有原理简单，计算量小的特点。克服了利用传统高分辨率网格创建水面方法计算量大的缺点。本方法形成的动态水面可以与三维地形等模型一起渲染，可以得到很好的整体效果。

[1]Peachey D.Modeling waves and surf[J].Computer Graphics，1986，20（4）：65-74.

[2]Fournier A，Reeves W T.A simple model of ocean waves[J].Computer Graphics，1986，20（4）： 75-84.

[3]Foster N，Metaxas D.Realistic animation of liquids[J].Graphical Models and Image Processing，1996，58（5）：471-483.

[4]Perlin K.An image synthesizer[J].Computer Graphics，1985，19（3）：287-296.

[5]Johanson C.Real-time water rendering-Introducing the projected grid concept[M].Sweden：Department of Computer Science，Lund University，Master dissertation，2004.

[6]杨怀平，孙家广.基于海浪谱的波浪模拟[J].系统仿真学报，2002，14（9）：1175-1178.

YANG Huai-ping，SUN Jia-guang.Waves simulation based on the wave spectrum of ocean.Journal of System Simulation，2002，14（9）：1175-1178.

[7]李广鑫，丁振国，詹海生，等.一种面向虚拟环境的真实感水波面建模算法 [J].计算机研究与发展，2004，41（9）：1580-1585.

LI Guang-xin，DING Zhen-guo，ZHAN Hai-sheng，et al.A modeling algorithm for realistic water surface simulation in virtual environment[J].Journal of Computer Research and Development，2004，41（9）：1580-1585.

[8]宋利，周源华，周军.基于Fourier合成技术的水波动画[J].计算机工程与应用，2002，（6）：10-11.

SONG Li，ZHOU Yuan-hua，ZHOU Jun.Waves animation based on fourier synthesis[J].Computer Engineering and Applications，2002，（6）：10-11.

[9]曹莉，李绍彬，申闫春.基于OSG的镜面反射特效的实现[J].计算机仿真，2009，26（8）：208-211.

CAO Li，LI Shao-bin，SHEN Yan-chun.Implementation of mirror reflection effect based on OSG[J].Computer Emulation，2009，26（8）:208-211.

[10]马骏，朱衡君，龚建华.基于Cg和 OpenGL的实时水面环境模拟[J].系统仿真学报，2006，18（2）：395-340.

MA Jun，ZHU Heng-jun，GONG Jian-hua.Simulation of realtime water surface based on Cg and OpenGL[J].Journal of System Simulation，2006，18（2）：395-340.