一种逻辑决策的排课算法
2012-09-26屈正庚
屈正庚
(商洛学院 计算机科学系,陕西 商洛 726000)
排课系统是一个典型的NP问题,是一个有约束的、非线性的、模糊多目标优化的、难解的、时空组合的数学问题[1-2]。怎样更好地体现学校各部门之间协同工作能力,怎样让学校的资源更合理化的使用,怎样使教师充分利用却又不疲倦,正是学校的排课系统需要解决的问题,针对这个方面文中提出了一种采用逻辑决策方式去解决实际生活中存在的问题,通过对0和1进行与和或运算,能得到一个合理的课表,也很容易解决排课过程中出现的冲突问题。实践证明得到了很好的效果。
1 解决排课问题的思路
1.1 基本思想
排课系统主要围绕学生、教师、教室、时间4个资源展开活动。在设计系统时,根据实际情况逐步细化每个环节、综合考虑全局利益、重视发挥整体效果、保证系统运行效率[3-5]。所以设计排课系统时力求保证系统的扩充性、灵活性、安全性、易操作性、易维护性等特征。
一般排课过程的基本思想是:
1)根据课程的性质、教师的使用情况、班级开课的多少确定某门课程的时间段。例如英语、专业课安排在早晨,每个班级课程分布均匀,避免在某一些天中没有上课的情况;
2)先后对班级和教师进行扫描,判断该时间段是否有空闲,如果有则给相应班级对应的课程确定教室;没有则重新分配资源;
3)当确定教室以后,检测对应的时间段是否有空余的教室,如果有则符合条件安排这门课程,否则更换资源信息。
1.2 解决问题的流程
排课问题就是对教师、班级、教室、时间等资源去争用并访问的问题,排课算法流程如图1所示。
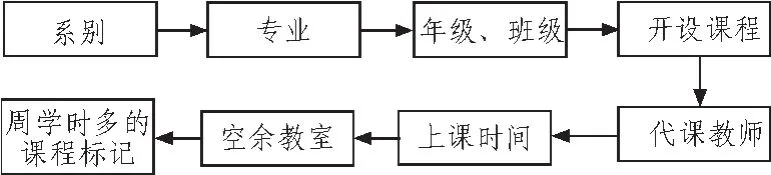
图1 排课流程Fig.1 Scheduling process
基本过程是:1)选择出该系别里的专业对应的年级和班级。列表出该班级在这一学期开设的课程;2)根据优先级的顺序选择课程,包括该课程总学时、周学时、主讲教师等信息。一般情况下先基础后专业,先大班后小班,先困难后容易;3)列出带此门课程的教师信息;4)根据班级情况、教师情况、课程的总学时和周学时确定上课时间段。这一步特别关键,是否产生冲突就在这个地方体现。在排列课表时要以人为本,系统利用边排列边检测的手段进行工作。同时,排课完成后最繁琐的工作就是资源检查和统计、冲突避免和调节;5)根据周学时选出可利用的教室。一门课程周学时多的尽量固定在一个教室里;6)对于周学时和总学时多的课程设置标记。例如对英语、数学等课程一周多次,在安排时至少隔一天,保证上课效果。
2 逻辑决策的排课算法
2.1 算法的思想
根据教学计划,列出每个班级开设课程的进度,建立一个教学进度数据库表。如果对于某一门课程需要合班时,也需要加上一条数据信息。对数据库中班级进度通过一个专用的标志来表示,包括该班级的课程、教师、时间、教室等信息。通过“0,1”字符串来实现排课过程。“0”表示资源未被占用,“1”表示资源已占用[6-7]。
2.2 算法的关键技术
假设09级计算机应用专业一班现在开设3门课程:公共英语、合班课马克思主义哲学、数据结构,对应的周学时分别为4、2、4,对应的教师分别是教师A、教师 B、教师C。按照一周5天上班,每天上课时间段为4大节课。安排课程时一次性连续上2小时。已知3位教师的教学时间和教室使用情况对应的信息字符串如表1所示。
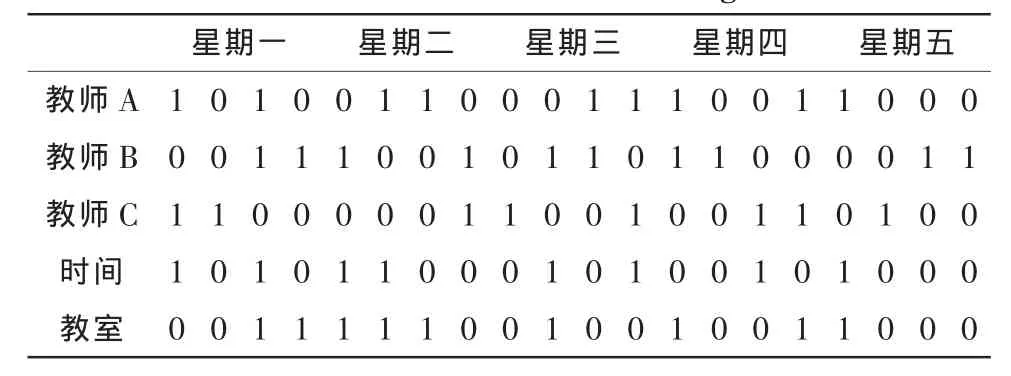
表1 信息字符串Tab.1 Information string
3位教师与时间和教室按位进行逻辑或运算,结果为“0”表示资源不发生冲突,对此班级安排课表如表2所示。

表2 教师课表Tab.2 Teachers curriculum
根据前面介绍的排课规律和基本原则可知,对这3门课程由高到低的方式排序:公共英语>马克思主义哲学>数据结构,英语尽可能在早晨,周学时为4的至少隔1天。经过全面思考与调整,首先教师C的数据结构只能放在周三(5-6)与周五(5-6)恰当,教师A的公共英语放在周一(3-4)与周四(3-4),教师B的马克思主义哲学放在周三(1-2)。
如果教师与时间和教室按位进行逻辑或运算,结果为“1”表示有冲突发生,则进一步对教师与时间和教室按位进行逻辑与运算,结果为“0”表示冲突可以解决,根据课程加权值进行排序,采用协商技术。结果为“1”表示最严重,就要转变决策,这时要回到初始状态,重新分配资源。
3 逻辑决策的算法实验结果
通过上面描述的算法思想和原理,给出了一个仿真系统,利用该系统对排列的课程进行认真分析、仔细的计算,得到了理想的结果,而且算法运行效率高。对发生的冲突解决起来速度快[8-10]。
假设现在只有2个教室供班级上课,一周上课时间5天,每天安排4大节课程,对班级的一周课程进行安排。教学安进度表如表3所示。

表3 班级课程信息表Tab.3 Class course information sheet
从表3中可以看出,3个班级一共开设了6门课程,每个班级一周上12节课程,共有6名教师。对这些数据按照逻辑运算的法则进行安排课表,结果如表4所示。
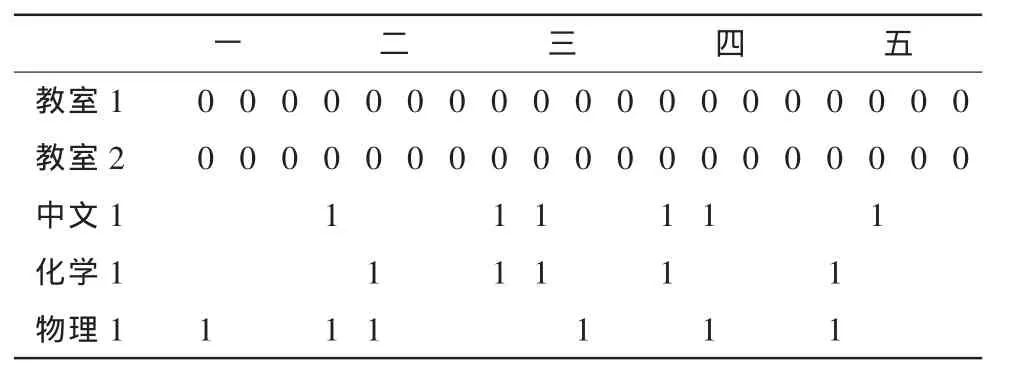
表4 班级课表Tab.4 Class curriculum
地理 1班:周一(1-2)上文学欣赏,周二(1-2)上基础数学,周三(1-2)上哲学,(3-4)上文学欣赏,周四(1-2)上公共体育,(3-4)上基础数学,周五(3-4)上经济学。
化学 1班:周一(1-2)上公共英语,周二(3-4)上文学欣赏,周三(1-2)上基础数学,(3-4)上公共英语,周四(1-2)上大学物理,周五(1-2)上基础等数学。
电子1班:周一(3-4)上经济学,周二(1-2)上公共英语,(3-4)上大学物理,周三(5-6)上公共体育,周四(3-4)上大学物理,周五(3-4)上公共英语。
4 结束语
从以上数据分析,该算法是符合实际要求的,采用此算法可以排列出可靠、满意、稳定的班级课表和教师课表,适合在高等学校使用[11-12]。因此,利用此算法提高管理水平,使教务处的工作变得更加科学化和规范化。该算法以人为本,满足教务处教师、学生及管理人员不同需求,提高资源的利用率,保证课程的教学效果,加强学校的教学质量。
[1]杨东风.自愿选课算法分析与优化研究[J].电子设计工程,2011,19(5):108-110.
YANG Dong-feng.Volunteers course algorithm analysis and optimization research[J].Electronic Design Engineering,2011,19(5):108-110.
[2]祝勇仁,曹焕亚.应用遗传算法求解排课问题[J].计算机应
用与软件,2007, 24(12):130-132.
ZHU Yong-ren,CAO Huan-ya.Application of genetic algorithm to timetable problem[J].Computer Applications and Software,2007,24(12):130-132.
[3]李红婵,户刚,朱颢东.基于群体优势遗传算法的高校排课问题研究[J].计算机工程与应用,2011,47(8):1235-1237.
LI Hong-chan,HU Gang,ZHU Hao-dong.Research of UTP based on population dominant GA[J].Computer Engineering and Applications,2011,47(10):233-236.
[4]金保华,李红婵.采用新型编码GA的高校排课问题仿真研究[J].计算机工程与应用,2011,47(13):1066-1069.
JIN Bao-hua,LI Hong-chan.Simulation study of UTP with new code GA[J].Computer Engineering and Applications,2011,47(13):1066-1069.
[5]张立岩,张世民,秦敏.基于改进粒子群算法排课问题研究[J].河北科技大学学报,2011,32(3):55-58.
ZHANG Li-yan,ZHANG Shi-min,QIN Min.Research in improved particle swarm optimization for schedule arrangement[J].Journal of Hebei University of Science and Technology,2011,32(3):265-269
[6]高武奇,康凤举,钟联炯.基于冲突检测算法的二级排课系统[J].西安工业大学学报,2008,5(28):506-509.
GAO Wu-qi,KANG Feng-ju,ZHONG Lian-jiong.Two-level course arrangement system with collision detection algorithm[J].Journal of Xi’an Technological University,2008,5(28):506-509.
[7]徐成刚,易军凯,肖洋.基于约束逻辑程序设计的排课算法研究[J].计算机工程与应用,2006,42(31):197-199.
XU Cheng-gang,YI Jun-kai,XIAO Yang.Constraint logic programming-based course timetabling algorithm[J].Computer Engineering and Applications,2006,42(31):197-199.
[8]王凤,林杰.高校排课问题的图论模型及算法[J].计算机工程与应用,2009,45(27):240-242.
WANG Feng,LIN Jie.Model of college time-table problem based on graph theory[J].Computer Engineering and Applications,2009,45(27):240-242.
[9]王军,陈建云.基于C#舟运用遗传算法的排课系统[J].电子设计工程,2010,12(18):85-88.
WANG Jun,CHEN Jian-yun.Apply genetic algorithm to design timetabling system based on C sharp[J].Electronic Design Engineering,2010,12(18):85-88.
[10]滕姿,邓辉文,杨久俊.基于遗传算法的排课系统的设计与实现[J].计算机应用,2007,27(12):199-201.
TENG Zi,DENG Hui-wen,YANG Jiu-jun.Timetabling system’s design and implementation based on the genetic algorithm[J].Journal of Computer Application,2007,27(12):199-201.
[11]韦玉,冯速.免疫遗传算法在排课问题中的应用[J].北京师范大学学报,2008,44(2):168-172.
WEI Yu,FENG Su.The application of immune genetic algorithm in the problem of timetabling[J].Journal of Beijing Normal University,2008,44(2):168-172.
[12]GUO Hong-bin,YAN Jing-feng.Research ofuniversity course scheduling system based on evolutionary algorithm[C]//
The 3rd International Conference on Computational Intelligence and Industrial Application (PACIIA2010),2010:238-240.
