K-means聚类算法研究综述

王 千， 王 成， 冯振元，叶金凤

（1.69026部队 新疆 乌鲁木齐 830002；2.西安交通大学 航天航空学院，陕西 西安 710049；3.中国建设银行 苏州常熟支行，江苏 常熟 215500）

K-means聚类算法是由Steinhaus 1955年、Lloyd 1957年、Ball&Hall 1965年、McQueen 1967年分别在各自的不同的科学研究领域独立的提出。K-means聚类算法被提出来后，在不同的学科领域被广泛研究和应用，并发展出大量不同的改进算法。虽然K-means聚类算法被提出已经超过50年了，但目前仍然是应用最广泛的划分聚类算法之一[1]。容易实施、简单、高效、成功的应用案例和经验是其仍然流行的主要原因。

文中总结评述了K-means聚类算法的研究现状，指出K-means聚类算法是一个NP难优化问题，无法获得全局最优。介绍了K-means聚类算法的目标函数、算法流程，并列举了一个实例，指出了数据子集的数目K、初始聚类中心选取、相似性度量和距离矩阵为K-means聚类算法的3个基本参数。总结了K-means聚类算法存在的问题及其改进算法，指出了K-means聚类的进一步研究方向。

1 经典K-means 聚类算法简介

1.1 K-Means聚类算法的目标函数

对于给定的一个包含 n个d维数据点的数据集X={x1，x2，…，xi，…，xn}，其中 xi∈Rd，以及要生成的数据子集的数目K，K-Means聚类算法将数据对象组织为K个划分C={ck，i=1，2，…K}。每个划分代表一个类ck，每个类ck有一个类别中心μi。选取欧氏距离作为相似性和距离判断准则，计算该类内各点到聚类中心μi的距离平方和

显然，根据最小二乘法和拉格朗日原理，聚类中心μk应该取为类别ck类各数据点的平均值。

K-means聚类算法从一个初始的K类别划分开始，然后将各数据点指派到各个类别中，以减小总的距离平方和。因为K-means聚类算法中总的距离平方和随着类别个数K的增加而趋向于减小（当 K=n时，J（C）=0）。因此，总的距离平方和只能在某个确定的类别个数K下，取得最小值。

1.2 K-means算法的算法流程

K-means算法是一个反复迭代过程，目的是使聚类域中所有的样品到聚类中心距离的平方和J（C）最小，算法流程包括4个步骤[1]，具体流程图如图1所示。

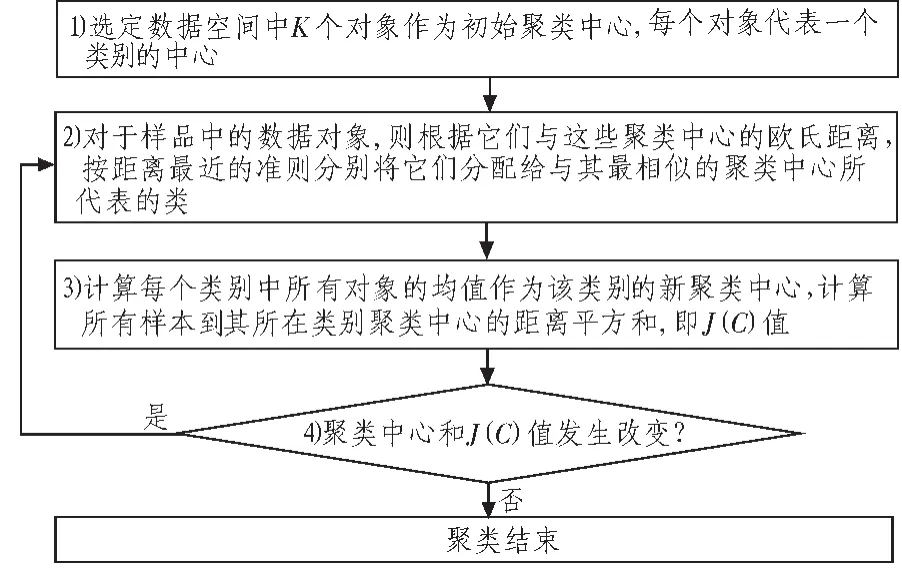
图1 K-means聚类算法流程图Fig.1 Steps of K-means clustering algorithm

1.3 K-means聚类算法实例

图2显示的是K-means算法将一个2维数据集聚成3类的过程示意图。

2 K-means聚类算法是一个NP难优化问题

K-means聚类算法是一个NP难优化问题吗?在某个确定的类别个数K下，在多项式时间内，最小的总距离平方和J（C）值和对应的聚类划分能否得到？目前，不同的学者有不同的答案。

Aristidis Likas等人[2]认为在多项式时间内最小的值和对应的聚类划分能够得到，并于2002年提出了全局最优的K-means聚类算法。但给出的 “The global k-means clustering algorithm”只有初始聚类中心选取的算法步骤，而缺乏理论证明。 很快，pierre Hansen等人[3]就提出“The global k-means clustering algorithm”不过是一个启发式增量算法，并不能保证得到全局最优，文章最后还给出了反例。

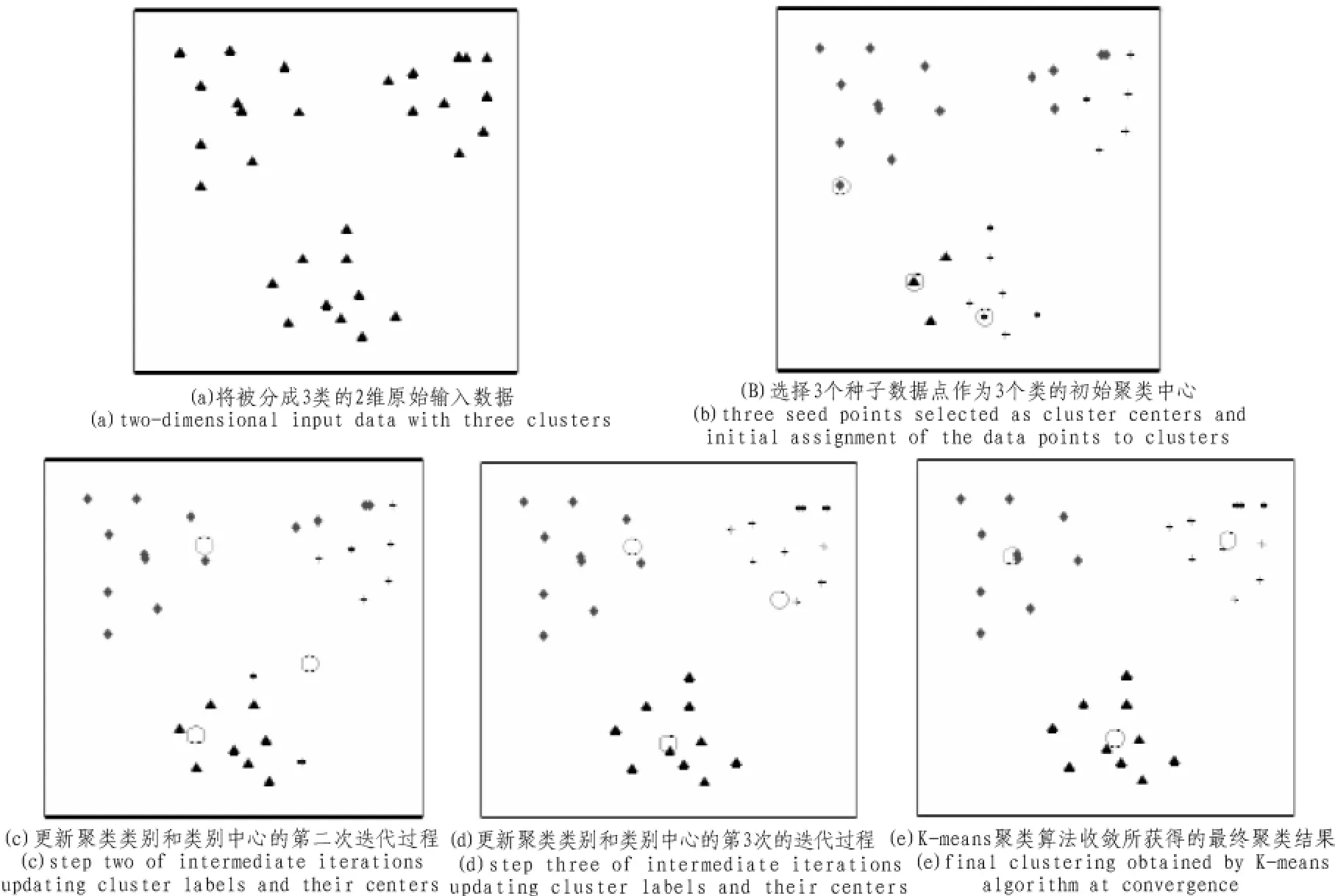
图2 K-means算法示意图Fig.2 Illustration of K-means algorithm

很多学者指出，如果数据点的维数d=1，最小的总距离平方和J（C）值和对应的聚类划分能够在O（Kn）2时间内使用动态规划获得，例如Bellman and Dreyfus[4]。Pierre Hansen等人[3]认为，K-means聚类算法时间复杂度未知。

但是，更多的学者认为，对于一般的数据维数d和类别个数K，K-means聚类算法是一个NP难优化问题[5]。Sanjoy Dasgupta等人认为即使在类别个数K=2的情况下，K-means聚类算法也是一个NP难优化问题。Meena Mahajan等人[6]认为即使在数据点的维数d=2下，对于平面的K-means聚类问题，也是NP难的。本研究也认为，对于一般的数据维数d和类别个数K，K-means聚类算法是一个NP难优化问题。K-means聚类算法是一个贪心算法，在多项式时间内，仅能获得局部最优，而不可能获得全局最优。

3 K-means聚类算法的参数及其改进

K-means聚类算法需要用户指定3个参数：类别个数K，初始聚类中心、相似性和距离度量。针对这3个参数，K-means聚类算法出现了不同的改进和变种。

3.1 类别个数K

K-means聚类算法最被人所诟病的是类别个数K的选择。因为缺少严格的数学准则，学者们提出了大量的启发式和贪婪准则来选择类别个数K。最有代表性的是，令K逐渐增加，如K=1，2，…，因为K-Means聚类算法中总的距离平方和J随着类别个数K的增加而单调减少。最初由于K较小，类型的分裂（增加）会使J值迅速减小，但当K增加到一定数值时，J值减小速度会减慢，直到当K等于总样本数N时，J=0，这时意味着每类样本自成一类，每个样本就是聚类中心。如图3所示，曲线的拐点A对应着接近最优的K值，最优K值是对J值减小量、计算量以及分类效果等进行权衡得出的结果。而在实际应用中，经常对同一数据集，取不同的K值，独立运行K-means聚类算法，然后由领域专家选取最有意义的聚类划分结果。

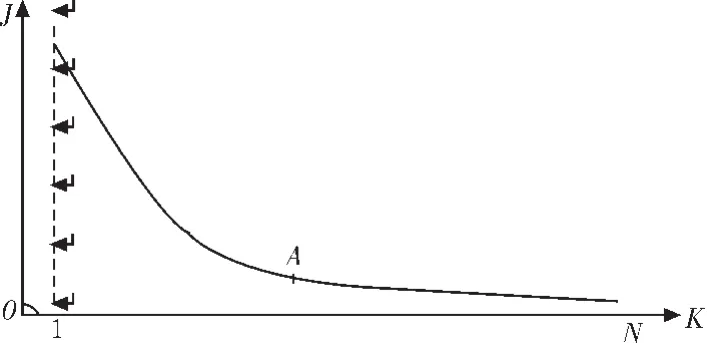
图3 J-K关系曲线Fig.3 Relationship curve between J and K

并非所有的情况都容易找到J-K关系曲线的拐点，此时K值将无法确定。 对类别个数K的选择改进的算法是Ball&Hall[7]于1965年提出的迭代自组织的数据分析算法（Iterative Self-organizing Data Analysis Techniques Algorithm，ISODATA），该算法在运算的过程中聚类中心的数目不是固定不变的，而是反复进行修改，以得到较合理的类别数K，这种修改通过模式类的合并和分裂来实现，合并与分裂在一组预先选定的参数指导下进行。

3.2 初始聚类中心的选取

越来越对的学者倾向于认为最小化总距离平方和J（C）值和对应的聚类划分是一个NP难优化问题。因此，K-means聚类算法是一个贪心算法，在多项式时间内，仅能获得局部最优。而不同的初始聚类中心选取方法得到的最终局部最优结果不同。因此，大量的初始聚类中心选取方案被提出。

经典的K-means聚类算法的初始聚类中心是随机选取的。Selim S Z，Al-Sultan K S于1991年提出的随机重启动K-means聚类算法是目前工程中应用最广泛的初始聚类中心选取方法，其过程如图4所示。王成等人提出使用最大最小原则来选取初始聚类中心[8]，与其它方法不同的是，该过程是一个确定性过程。模拟退火、生物遗传等优化搜索算法也被用于K-means聚类算法初始聚类中心的选取。四种初始聚类中心选取方法的比较可见文献[9]。自从Aristidis Likas等人[2]提出“The global k-means clustering algorithm”，对其的批评[3]、讨论和改进就没有停止过[10]。

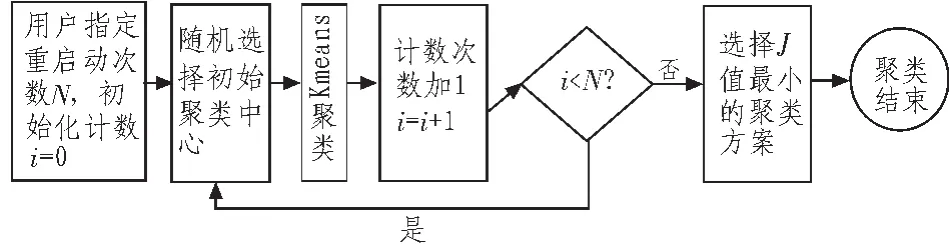
图4 多次重启动K-means聚类算法流程图Fig.4 Steps of multiple restarts K-means clustering algorithm

3.3 相似性度量和距离矩阵

K-means聚类算法使用欧式距离作为相似性度量和距离矩阵，计算各数据点到其类别中心的距离平方和。因此，K-means聚类算法划分出来的类别都是类球形的。实际上，欧式距离是Minkowski距离在m=2时的特例，即L2距离。在采用Lm距离进行K-means聚类时，最终类中心应是每一类的m中心向量。Kashima等人于2008年使用L1距离，最终聚类中心使每一类的中位向量。 对于一维数据集 X={x1，x2，…，xi，…，xn}而言，中位数M比均值x¯对异常数据有较强的抗干扰性，聚类结果受数据中异常值的影响较小。Mao&Jain[11]于1996年提出使用Mahalanobis距离，但计算代价太大。在应用中，Linde等.于 1980年提出使用Itakura-Saito距离。Banerjee等人2004年提出，如果使用Bregman差异作为距离度量，有许多突出优点，如克服局部最优、类别之间的线性分离、线性时间复杂度等。

4 K-means聚类算法的其他改进

在K-means聚类算法中，每个数据点都被唯一的划分到一个类别中，这被称为硬聚类算法，它不易处理聚类不是致密而是壳形的情形。模糊聚类算法能摆脱这些限制，这些方法是过去20年间集中研究的课题。在模糊方法中，数据点可以同时属于多个聚类，Dunn等人[12]于1973年提出了模糊K-means聚类算法。

5 结束语

笔者也相信K-means聚类是一个NP难优化问题，但这需要更加严格的数学理论证明。因此，K-means聚类算法是一个贪心算法，在多项式时间内，仅能获得局部最优，对K-means聚类算法的研究也将继续。但是对K-means聚类算法的研究和改进应注意以下几点：

1）笔者感兴趣的是现实世界问题的实际解决方案，模式分析算法必须能处理非常大的数据集。所以，只在小规模的例子上运行良好是不够的；我们要求他的性能按比例延伸到大的数据集上，也就是高效算法（efficient algorithm）。

2）在现实生活应用中数据里经常混有由于人为误差而引起的噪声。我们要求算法能够处理混有噪声的数据，并识别近似模式。只要噪声不过多地影响输出，这些算法应能容忍少量的噪声，称为算法的健壮性（robust）。相对于L2距离，L1距离有较强的健壮性。但相似性度量和距离矩阵的选取，不是一个理论问题，而是一个应用问题，需要根据问题和应用需要需求，假定合适的模型。例如，采用不同Lm的距离，K-means聚类的结果一般是不同的。

3）统计稳定性即算法识别的模式确实是数据源的真实模式，而不只是出现在有限训练集内的偶然关系。如果我们在来自同一数据源的新样本上重新运行算法，它应该识别出相似的模式，从这个意义上讲，可以把这个性质看作输出在统计上的健壮性。样本读入次序不同，一些聚类算法获得的模式完全不同，而另一些聚类算法对样本读入次序不敏感。从这个角度来讲，最大最小原则比随机重启动、模拟退火、生物遗传在初始聚类中心选取上要好。

4）K-means聚类算法的很多变种引入了许多由用户指定的新参数，对这些参数又如何自动寻优确定，是一个不断深入和发展的过程。

5）K-means还存在一个类别自动合并问题[1]，在聚类过程中产生某一类中无对象的情况，使得得到的类别数少于用户指定的类别数，从而产生错误，能影响分类结果。其原因需要在理论上深入探讨，但这方面的论文和研究很少。聚类的意义，这也是所有的聚类算法都面临的问题，需要在数学理论和应用两方面开展研究。

[1]Anil K J.Data clustering:50 years beyond K-Means[J].Pattern Recognition Letters，2010，31（8）：651-666.

[2]Likas A，Vlassis M，Verbeek J.The global K-means clustering algorithm[J].Pattern Recognition，2003，36（2）:451-461.

[3]Selim S Z，Al-Sultan K S.Analysis of global K-means，an incremental heuristic for minimum sum-of-squares clustering[J].Journal of Classification，2005（22）:287-310.

[4]Bellman R，Dreyfus S.Applied dynamic programming[M].New Jersey：Princeton University Press，1962.

[5]Aloise D，Deshpande A，Hansen P，et al.NP-hardness of euclidean sum-of-squares clustering[J].Machine Learning，2009，75（2）：245-248.

[6]Mahajan M，Nimbor P，Varadarajan K.The planar K-means problem is NP-hard[J].Lecture Notes in Computer Science，2009（5431）：274-285.

[7]Ball G，Hall D.ISODATA，a novel method of data analysis and pattern classification[M].California：Technical rept.NTIS AD 699616.Stanford Research Institute，1965.

[8]WANG Cheng，LI Jiao-jiao，BAI Jun-qing，et al.Max-Min K-means Clustering Algorithm and Application in Post-processing of Scientific Computing[C]//Napoli：ISEM，2011：7-9.

[9]Pena J M，Lozano J A，Larranaga P.An empirical comparison of four initialization methods for the K-means algorithm[J].Pattern Recognition Letters，1999（20）：1027-1040.

[10]Lai J Z C，Tsung-Jen H.Fast global K-means clustering using cluster membership and inequality[J].Pattern Recognition，2010（43）：1954-1963.

[11]Mao J，Jain A K.A self-organizing network for hyperellipsoidal clustering（hec）[J].IEEE Transactions on neural networks，1996（7）：16-29.

[12]Dunn J C.A fuzzy relative of the isodata process and its use in detecting compact well-separated clusters[J].Journal of Cybernetics，1973（3）：32-57.