基于关系代数树的查询优化方法实例分析

冯凯平，李晓良

（1.四川烹饪高等专科学校信息技术系 四川 成都 610072；2.中国科学院上海微系统与信息技术研究所 上海 200050）

基于网络的自适应性测试是一种先进的考试方式，在考试过程中，系统对题库的访问频率很高，当参试者较多时，对数据库的访问将更加频繁，特别是随着数据库不断增容，数据库中的数据量迅猛增长，这将导致数据库系统的性能下降，直接影响到系统的性能及应用。因此，数据库查询速率的高低成为决定自适应测试成功与否的重要因素之一。

基于关系代数树的查询优化方法，其基本思想是将选择、连接等操作的运算符在遵循关系代数等价变换规则的原则下，尽可能深地移到关系树的底部[1]。对使用诸如SQL的某种语言书写的查询进行语法分析，将查询语句转换成按某种有用方式表示查询语句结构的关系代数树，把关系代数树转换成基于关系代数表达式的逻辑查询计划[2]。

1 关系代数等价变换规则

设R和S各表示一个关系、πL为投影（L为投影属性）、σC为选择 （c为选择条件）、δ为消除重复、γL为聚集与分组（L为属性）、∞C为连接（c为连接条件）、×为关系的积。

1.1 涉及选择的定律

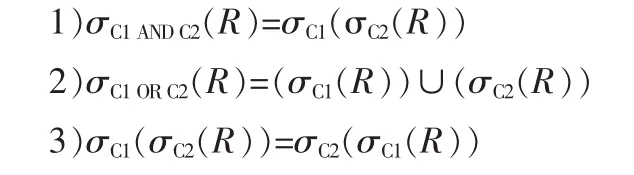
对涉及两参数的选择定律：

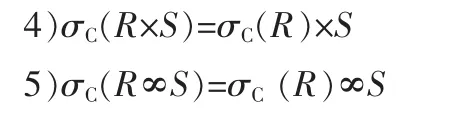
1.2 涉及投影的定律

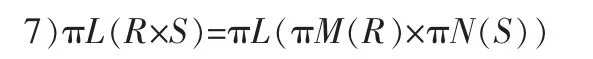
1.3 有关连接和积的定律

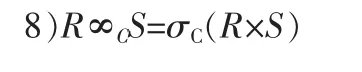
2 查询计划的改进

将关系代数操作符进行组合，把一个操作符应用到其他的一个或多个操作符之上形成一个表达式树。这棵树的叶节点是关系的名字，内部节点被标记为操作符，这个操作符应用到它的子女代表的关系上。通过各个操作符的上移或下移，实现查询优化[1-4]。

2.1 实例1

查询答对难度级别为2的某道题目的所有考生。

假设有以下关系：

TitleTable（题目号，答案，难度，区分度，猜度，类别，……）

AnswerTable（考生姓名，题号，作答，bInit，……）

对于关系AnswerTable，每答一道题产生一个元组。

1）按关系的乘积查询

select考生姓名

from TitleTable，AnswerTable

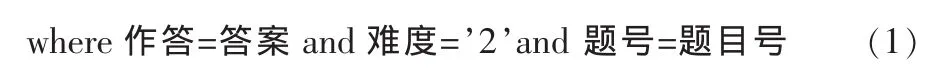
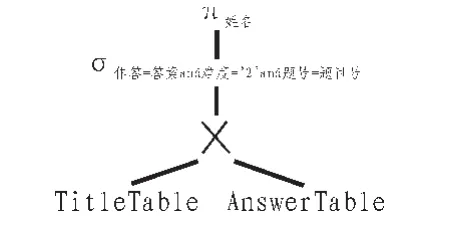
图1 由式（1）对应的逻辑查询计划Fig.1 By type（1） the corresponding logic inquires the plan

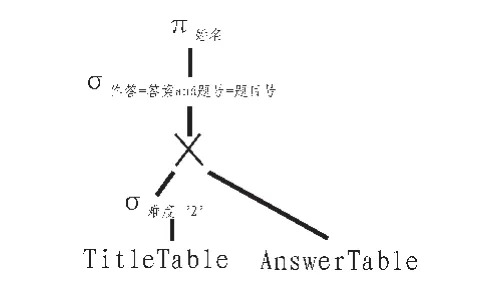
图2 对图1的一个改进查询计划Fig.2 In figure 1 improvement inquires the plan

式（1）所对应的代数树结构如图1所示。在这个逻辑查询计划中，首先在最底层实行两个数据表的积，通过使用乘积操作符来连接FROM列表中的关系。下一步做一个表示WHERE子句的选择操作，最后一步是投影到SELECT子句的列表上。

为了实现相同的操作，并提高查询效率，可以将选择操作符σ尽量下移[1-3]，其依据来自于关系表达式等价变换规则①和④。如图2所示为一个改进了的查询计划。在这个计划中，由于提前对数据表TitleTable关于难度值进行了筛选，减少了关系积的规模[3]，使得查询速率得以提高。

经过在 HP6500服务器、WINDOWSE 2000 SERVER操作系统平台、SQL SERVER环境下测试，查询速率提高大约65-75%。事实上，由于查询优化器的作用，其效率的提高远不止于此。

其对应的SQL语句如式（2）。

select考生姓名

from （select*from TitleTable where 难度=’2’）as a，Answer-Table as b

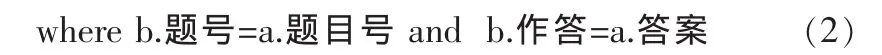
2）按关系的连接查询

根据等价变换规则⑧，可将图1的关系积转换为图3的关系连接，此关系代数树实现相同的结果。在树中，WHERE子句中的条件“题号=题目号”应用到两个关系的乘积上，成为等值连接，形成将一个选择和一个乘积结合成一个连接的操作。通常，连接比乘积产生的元组要少，因此，连接的查询效率要高于乘积的查询效率。对应的SQL语句如式（3）。

select考生姓名

from TitleTable as a inner join AnswerTable as b on b.题号=a.题目号

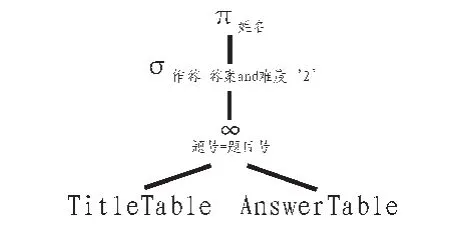
图3 基于连接的查询计划Fig.3 Based on the inquires connection plan

经测试，图3的查询速率比图1高10%左右，这主要是关系TitleTable中关于题号没有重复元组，否则图3的查询效率比图1会更高。

根据等价变换规则⑤将图3转换为图4，图4在图3的基础上得到了较大改进。

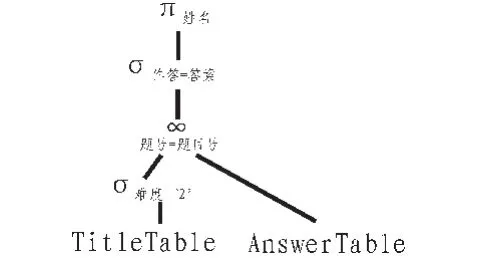
图4 对图3的改进查询计划Fig.4 In figure 3 improvement inquires the plan

2.2 实例2

查找对题目猜度最高并且答对该题的考生

1）带子查询的查询计划

带IN条件的代数树结构比较特殊，如图5所示，上方的σ操作符属于一个两参数选择，该结点之下有一个左子结点，它表示要对其做选择操作的关系AnswerTable；以及一个右结点，它表示作用到关系AnswerTable的每个元组上的条件表达式。

图5和式（4）分别示出其关系代数树和SQL表达式。

select考生姓名

from AnswerTable

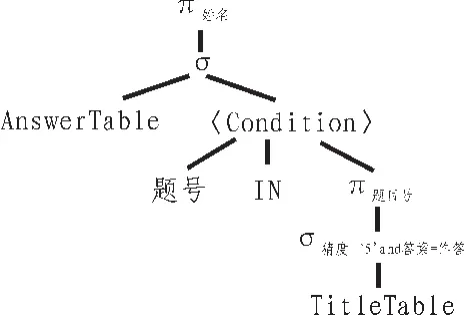
图5 应用IN条件Fig.5 Application condition IN

2）去除子查询的查询计划

存在IN条件的代数表达式通常出现在子查询中。

在实际操作中尽量避免子查询[5]，否则，将子查询应用到关系中的每个元组时都要计算一篇子查询，这无疑是一笔巨大的开销。

消除IN条件的基本方法如下：

假设有一个两参数选择（图5上方的σ），其中第一个参数为 R，第二个参数是形如t IN S的＜Condition＞，t是R的（某些）属性组成的一个元组，按如下方式对树作变换：

a）用S的表达式树替换＜Condition＞。

b）用一个单参数选择σC替换两参数选择 （图6上方的σ），其中C是元组t的每个分量与关系S中相应的属性取等值的条件。

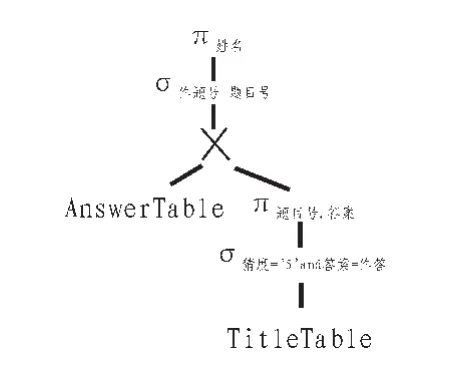
图6 去除IN条件Fig.6 Remove IN conditions

c）给一个参数，它是R与S的积。

根据以上规则，对图5进行相应变换，得到图6逻辑查询计划。表达式如式（5）。

select考生姓名

from AnswerTable as a，（select题目号， 答案 from Title Table where猜度=”5”）as b

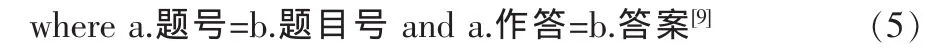
经测试，按图6建立的查询计划比图5查询速率提高大约70%。

为了进一步提高查询速率，对图6的乘积操作，可按图1到图3的变换规则变换成连接操作。

2.3 实例3

为了确定题目的有效度，需要查找作答了某道题所有考生的平均特质水平与该试题难度级别接近的题目。

数据表如下：

AnswerTable（考生姓名，题号，作答，bInit，……）

StudentTable（姓名，地址，性别，特质水平，……）

将平均特质水平与难度参数值之差的绝对值小于0.3作为确认标准，其SQL表达式如式（5）。

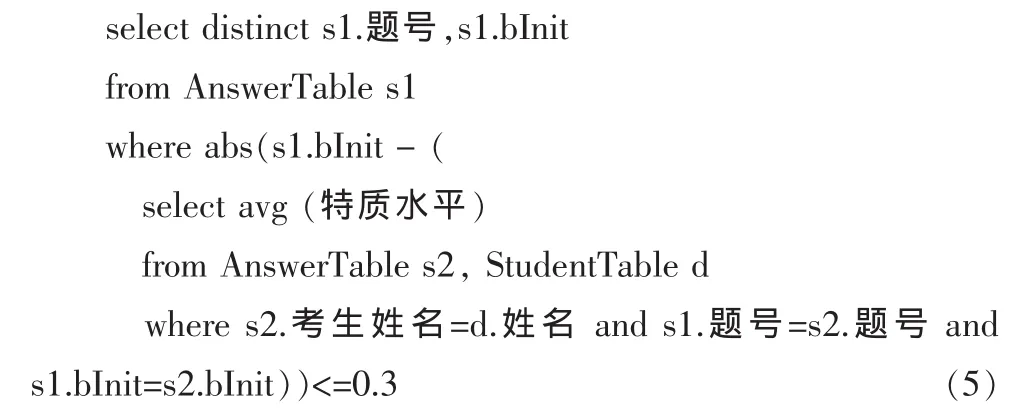
在式（5）所对应的关系代数树中，如图7所示，把子查询的WHERE子句分解成两个，并使用该子句的一部分把关系的积转换成等值连接。在这棵树的结点上使用了别名s1、s2、d。代数表达式在代数树的顶部结束，投影到所期望的属性上并消除重复。

图7 把式（5）转换成逻辑查询计划Fig.7 Mules（5） convert logic inquires the plan

图7是可以改进的，条件是：

1）δ在树的顶部；

2）AnswerTable s1中的“考生姓名”不出现在投影 πs1.题号，s1.bInit中；

3）AnswerTable s1与它的连接对象（图7中的右下部分）之间的连接能够将 AnswerTable s1中的“题号”、“bInit”属性与AnswerTable s2中的属性取等值。

由于这些条件均成立，则可以分别用 “s2.题号”、“s2.bInit”替换“s1.题号”、“s1.bInit”。 因此，图 7 中的上方的一个连接符可以去除。改进后的逻辑查询计划如图8所示。

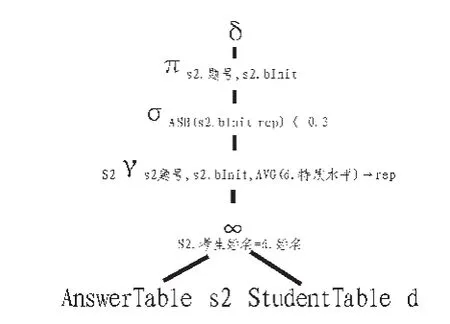
图8 图7的简化Fig.8 Figure 7 simplification

2.4 查询优化原则小结

1）选择σ应尽可能下移到表达式树中的下方。如果一个选择条件是多个条件用and连接，则可以把该条件分解并分别将每个条件下移。

2）投影π也可被下移到树中的下方，可加入新的投影。

3）消除重复δ有时可以不用，或者移到更方便的位置。

4）某些σ可以与其下方的积相结合以便把操作转换成等值连接。

3 操作代价的估计

图3对两个关系TitleTable、AnswerTable分别进行投影、选择和连接。投影的代价是可以精确估计的，而选择代价和连接代价需要通过“统计量收集”过程来估计[1-6，8]。

3.1 投影大小的估计

对于关系 AnswerTable（考生姓名，题号，作答，bInit），并在以下简称为An。假设4个属性的长度分别为 6、4、1、1个字节，设每个元组的头需要12字节，如此，关系An的每一个元组占24字节。设块为2 048字节长，其中块头占24字节。因此，每块可存放168个元组。假设总的元组数为10 000，即T（An）=10 000，需要的块数为 60，即 B（An）=60。

现在考虑投影S=π姓名（An），关系S的元组长度仅为6字节长，而T（S）仍为10 000。但是，现在却可以在一个块中放入 337 个元组，故 B（S）=30。

从而该投影缩减了关系约1倍，显著减少了系统的I/O操作频率，加快了DBMS扫描器扫描速率[3]。

3.2 连接大小的估计

对于关系TitleTable（题目号，答案），并在以下简称为Ti，假设共计8 000个元组。

用V（Ti，题目号）表示Ti中“题目号”属性不同值的元组种类数目。由于Ti关于题目号无重复元组，所以V（Ti，题目号）=8 000。然而，对于An关于题号是有重复的，其重复度需要根据参试人数、试卷的题量、考生的特质水平级别数来确定。

作以下假定：

1）根据全校可试机器台数，假设一次参试人数为500人。

2）在自适应性测试中，每位参试者的题量是不等的，假设平均值为20道题。

3）每位参试者的特质水平不同，简单地分为5级。

一次考试系统总抽题量为T（An）=20×500=10 000。 考虑到每个考生特质水平的不同，所答题目的级别也不同，同一题目在不同特质水平考生中的分布系数大约为4/5=0.8，因此，每道题被抽取的概率大约为20×0.8/8 000=0.002，出现的次数为 0.002×10 000=20。 V（An， 题号）被确定为

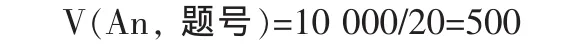
最终对连接后元组数T（An∞Ti）的估计为

T（An∞Ti）=T（An）T（Ti）/Max（V（An， 题号），V（Ti， 题目号））[1]=10 000×8 000/Max（500，8 000）=10 000

根据题目元组大小、磁盘页面大小、每页元组行数，DBMS扫描器在连接An、Ti的过程中至少全表扫描磁盘大约800 万次[3-9，10]。

3.3 选择大小的估计

图3所涉及的选择是逻辑等值比较，其大小相对容易估算。

假设题库中每道题目均仅有A、B、C、D 4种答案，并且4种答案是均匀分布的。因此，在发生了连接的关系An∞Ti中，逻辑表达式“作答=答案”就只有4种情形，按3/4的答对率计算，令x=4/3。另假设题目的难度级别有5种，令y=5。

已知 T （An∞Ti）=10 000。 对于 S=σ 作答=答案 and 难度=’2’（An∞Ti）， 通过下式求得经选择后新关系 S的元组数目：

分别将 x、y 代入（6）式，得 T（S）=10 000/x/y=1 500。

3.4 优化后的代价估计

采用类似的方法对图4进行大小估计。但是，由于优化后，关系Ti与An的共同属性值题目号违反了“值集的保持[1]”的假设，其估计值不太准确。可按以下方法大致估计：

在图 4查询计划中，对 Ti先进行选择 σ难度=’2’操作，假设难度值按均匀分布考虑，得到 T（Tiσ）=8 000/5=1 600。

此时再将其与关系An按题号连接，DBMS扫描器仅需扫描160万次即可，较大幅度地实现了优化。再向上进行σ作答=答案操作，仍能得到 T（S）=1 500。

4 结束语

SQL查询优化的实质就是在结果正确的前提下，用优化器可以识别的语句，尽量减少表扫描的I/O次数，进而减少表搜索。在数据库的管理、开发和应用过程中，SQL查询语句性能的优劣直接影响整个信息系统的效率，特别是大型数据库优化过程更为重要，其效率高的查询语句和效率低的查询语句速度相差可以达到几倍甚至上百倍。文中以应用实例为基础，以关系代数树结构为主线，结合数据库理论对关系数据库的查询优化机制，分析并实现对SQL语句的优化，进而保证数据库高效可靠地运行。

[1]Molina H G，Ullman J D，Widom J.Database system implementation[M].Palo Alto， California:Stanford University，2007.

[2]司训练，徐文静.代数树架构下高价谓词查询优化机制的算法设计[J].情报杂志，2007（1）：61-63.

SI Xun-lian，XU Wen-jing.Algorithm design of expensive predicate query optimization mechanism based on algebra tree framework[J].Intelligence magazine，2007（1）：61-63.

[3]王峥，王亚平.关系代数与SQL查询优化的研究[J].电子设计工程，2009，17（8）：110-112.

WANG Zheng，WANG Ya-ping.Research on relational algebra and SQL query optimization[J].Electronic Design Engineering，2009，17（8）：110-112.

[4]徐丽萍，金雄兵.一个并行查询优化器的设计与实现[J].计算机工程与科学.2007，29（2）：104-106.

XU Li-ping，JIN Xiong-bing.Design and realizat ion of a parallel query opt im izer[J].Computer Engineering&Sciencf，2007，29（2）：104-106.

[5]孙海东，张杨.一种分布式数据库多属性划分查询优化算法[J].微计算机应用，2010，31（3）：47-49.

SUN Hai-dong，ZHANG Yang.A distributed database query optimization algorithm for multi-attribute classification[J].Microcomputer Applicati NS，2010，31（3）：47-49.

[6]曲卫民，孙乐.XML数据查询中值匹配查询代价估计算法[J].软件学报，2005，16（4）：561-569.

QU Wei-min，SUN Le.A result size estimation algorithm for value predication in XML query[J].Journal of Software，2005，16（4）：561-569.

[7]吴胜利，王能斌.面向对象数据库中查询代价的估算[J].计算机研究与发展，1998，35（1）：69-73.

WU Sheng-li，WANG Neng-bin.Estiation of query cost in object-oriented database systems[J].Computer Research&Development，1998，35（1）：69-73.

[8]伍军云，徐少平.一种新的关系数据库查询优化方法[J].计算机与现代化，2006（7）：33-35.

WU Jun-yun，XU Shao-ping.A new query processing optimization algorithm based on statistic[J].Computer&Modernzation，2006（7）：33-35.

[9]佚名.数据库优化查询计划方法 [EB/OL].[2010-08-26].http://wenku.baidu.com/view.

[10]樊新华.关系数据库的查询优化技术[J].计算机与数字工程，2009，37（12）：188-190.

FAN Xin-hua.Optimizati on technology for queries in relational database[J].Computer&Digital Engineering，2009，37（12）：188-190.

[11]刘云生，彭楚冀.一种实时数据库查询执行方法的设计[J].计算机应用，2005，25（2）：279-282.

LIU Yun-sheng，PENG Chu-ji.Design of a query execution method for real-time database[J].Computer Applications，2005，25（2）：279-282.