城市交叉路口分级模糊控制器设计

2012-09-26宋美剑

物流技术 2012年13期

陆琳，张虹，宋美剑

（贵州财经大学，贵州贵阳 550004）

1 引言

经济社会的迅速发展给城市交通带来了巨大压力，常用的扩大交通基础设施建设的做法因受制于政府财政约束，作用空间已不大，在现有城市硬件设施的基础上，利用现代信息技术开发城市智能交通管理和控制系统对解决目前日益紧张的城市交通问题就显得尤为必要了。Chiu[1]设计了一个双输入双输出的模糊决策系统用于多交叉口交通网络；刘智勇[2]提出一种递阶模糊神经网络交通控制方法，采用控制子系统和协调层以提高控制精度。现有文献所构建模型主要是采用结构参数固定的模糊控制系统，对于复杂环境下的城市交通控制问题，不确定因素和子系统间的相互藕合作用增多，结构参数固定的模糊控制系统显然无法处理此类问题。针对这一问题，本文提出了一种新的分级模糊控制器，用于交叉路口交通流的控制与优化。

2 分级模糊控制器设计及应用

2.1 分级模糊控制器结构

分级模糊控制器的效能在于有效减少规则数，易于提取模糊规则。基于这一思想，设计分级模糊控制器如图1所示。

在图1中，绿灯增益模块和红灯损失模块（第一级模块）分别根据各车道上安装的信号检测器检测该车道的交通信息情况，并通过该信息来判断当前该模块交通流方向的交通拥堵状况，确定绿灯增益模块繁忙度和红灯损失模块的紧急度，并且两模块同时将确定结果传输给判决模块（第二集模块），再由判决模块比较两模块的的繁忙度和紧急度，决定当前绿灯是否调整跳转。绿灯增益模块的输入量采用当前绿灯相位信号灯转换的瞬间为起点开始计时，记录下在规定时间内通过该车道的车辆数作为变量X的论域，t=10S。红灯损失模块的输入量是采用当前红灯相位的上游车道检测器所检测到的排队等待通行的车辆数和红灯持续累计时间作为变量Y的论域。绿灯增益模块的输出为绿灯繁忙度，红灯损失模块的输出为红灯紧急度。第二级的判决模块根据第一级两个模块输出量的信息，在经过一系列的模糊推理运算后，将所得的结果做出判断对比，从而决定绿灯是否调整跳转，做出相应的模糊决策，并把该决策模糊化为一个实数值输出，其范围取(0～1)。当被反模糊化后的这个实数值超过某个特定值时，绿灯调整跳转，否则绿灯保持不变。

2.2 模糊规则的设计与提取

（1）在绿灯增益模块中，为了实现模糊控制将离开车辆数模糊化，需要将绿灯时间分为A,B两部分：A部分主要采集交叉路口当前相位上车辆状态参数，采集时间为10s；B部分是对模糊决策的延时，判断依据为当前两个方向车流量的变化量。同时保证车辆的行车速度不超过25km/h，则在10s内通过该路口的车辆数大约为10辆，计时起点均以当前绿灯相位的信号灯转换的瞬间为准，变量X的论域为10s内通过的车辆数，取(1-10)，并将其分为五个模糊子集:很少、少、中等、多、很多，其从属函数如图2所示。

（2）在红灯损失模块中，因为影响输入量Y的变化论域为到达车辆数的车队排队长度。以贵阳市某些路段的交叉路口在不同时段车流量的实测数据为依据分析，本系统的检测距离为100m左右。通常情况下，车辆间距与车辆本身的长度平均为5m左右，所以输入量Y的变化论域为(0-20)。并将其分为五个模糊子集: 很多、多、中等、少、很少，其从属函数如图3所示。

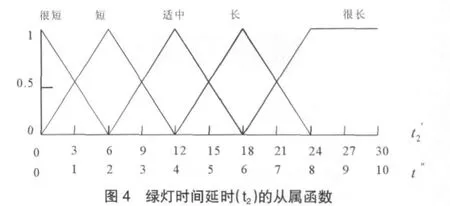
（3）本系统以不同相位间交通信号灯的转化作为系统的输出量。且各个相位间的关系都在于对当前绿灯的延时。贵阳市某些路段的交叉路口在不同时段车流量的实测数据为依据分析，本系统对直行取30s，左行取10s，则该相位绿灯延时的论域分别为(0-30)和(0-10)，并将其分为5个模糊子集：很长、长、适中、短、很短，其从属函数如图4所示。

（4）本系统采用矩阵方式对模糊控制规则进行设计，并根据现有相关知识和交警的实际操作来确定本系统的模糊规则。其具体控制规则见表1。

在表1中，当绿灯增益模块和红灯损失模块方向间的车流状态处于互补时，本系统对绿灯的延时均取“适中”，其目的是为了保证两个模块在车流量相差不多的情况下，尽可能快速地均衡疏散当前的车流。表1中共包含了如下多条条件语句：

规则1：X=很少，且Y=很少，则t2=很短；

规则2：X=很少，且Y=很少，则t2=很短；

规则3：X=很少，且Y=中等，则t2=很短；

规则4：X=很少，且Y=多，则t2=很短；

规则5：X=很少，且Y=多，则t2=很短；

规则6：X=少，且Y=很少，则t2=很短；

规则7：X=少，且Y=少，则t2=很短；

规则8：X=少，且Y=中等，则t2=短；

规则9：X=少，且Y=多，则t2=适中；

规则10：X=少，且Y=很多，则t2=长；

规则11：X=中等，且Y=很少，则t2=很短；

规则12：X=中等，且Y=少，则t2=短；

规则13：X=中等，且Y=中等，则t2=适中；

规则14：X=中等，且Y=多，则t2=长；

规则15：X=中等，且Y=很多，则t2=很长；

规则16：X=多，且Y=很少，则t2=短；

规则17：X=多，且Y=少，则t2=适中；

规则18：X=多，且Y=中等，则t2=长；

规则19：X=多，且Y=多，则t2=很长；

规则20：X=多，且Y=很多，则t2=很长；

规则21：X=很多，且Y=很少，则t2=适中；

规则22：X=很多，且Y=少，则t2=长；

规则23：X=很多，且Y=中等，则t2=很长；

规则24：X=很多，且Y=多，则t2=很长；

规则25：X=很多，且Y=多，则t2=很长。

运用模糊推理算法对结果进行还原计算，然后再输出精确量。

2.3 模糊隶属度函数调整方法

分级模糊控制器对较多的输入参数进行了分块分级处理，但仍然包含了较多的隶属度函数，若凭经验知识选取隶属函数，带有较大的主观性，并且，固定系统参数模糊控制器在应对大幅度波动交通流状况时，控制效果较差。根据交通的实际状况对模糊控制器隶属度函数进行自适应调整，并且利用智能优化算法调整分级模糊控制器的隶属度函数，可以改善控制系统的效果。源于遗传算法（GA）的分布估计算法（EDAs）是一种新的智能优化算法，其原理是采用群体中先进的个体，即适应度较高个体，然后统计其概率分布作为进化模型产生下一代子群，更能反映变量间的相互关系，准确度也更高。本文提出的分级模糊控制器运作采取如下步骤：（1）初始化隶属度函数，进行模糊控制；（2）统计交叉路口交通参数，计入历史数据库中；（3）交通流模拟器根据历史数据库交通参数模拟交通流，运用EDAs优化交通流模拟器，找出适合于当前交通流的模糊隶属度函数，将其送入模糊控制器加以更新。

2.4 仿真实验

以贵阳市中山路实测数据为依据，该交叉口为3*3，12条交通路段的十字路口。根据实测，车辆的平均时速为35km/h，车辆直行的统计概率为0.65，左转为0.2，右转为0.15。EDAs算法设置如下：N=2 000，Se=600。根据路段的实地调查，定时控制器平均通行车辆的平均等待时间为5.52s/辆，而采用分级模糊控制器通行车辆的平均等待时间缩短为4.67s/辆，优化达15.4%,显示该分级模糊控制器能提高道路的使用效率，效果较好。