巧用SPSS做均值向量检验

2012-09-26石岩涛

统计与决策 2012年12期

石岩涛

0 引言

为了实现用SPSS软件进行单总体均值向量的检验的目的，文[1]巧妙地运用了SPSS软件，成功地实现了对单总体均值向量的假设检验。在检验中，文[1]用到了SPSS运行后的一个结果，该结果是被称作F统计量的F值，再通过两总体均值的比较与单总体均值向量的假设检验间的Hotelling T2统计量T2、T1的关系转换求得T1的值，再利用T2分布的性质实现了均值向量的检验。文[1]的方法弥补了不能用SPSS软件直接做多元均值检验的缺憾。然而，均值向量的检验是可以通过F-检验法来实现的。如果在做均值向量的检验时，有一种方法能够更便捷地利用文[1]中得到的F值，那么，这种方法也更容易得到推广。

1 F1与F 2关系式的理论推导

由文[2]、[3]可知，正态总体的多元均值检验，是对假设

做检验。

即

且：

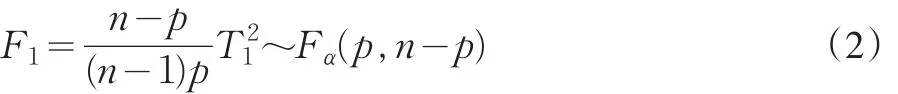
而在两总体均值比较的假设检验中，若假设两总体的协方差阵相等，则统计量：

其中，样本 X、Y皆来自p维正态总体，即X～N(μ1,Σ )、Y～N(μ2,Σ ) ；n1,n2是样本容量；协方差阵Σ的估计值：

其中，SX、SY为两样本的协方差阵；LX、LY是两样本离差阵。

当n1=n, n2=1时，随机样本Y就退化成一组观测，此时，两总体均值比较的假设检验就可视作单总体均值向量的检验，即：

而样本离差阵：

将（5）式代入（4）式有：

将（6）式代入（3）式得：

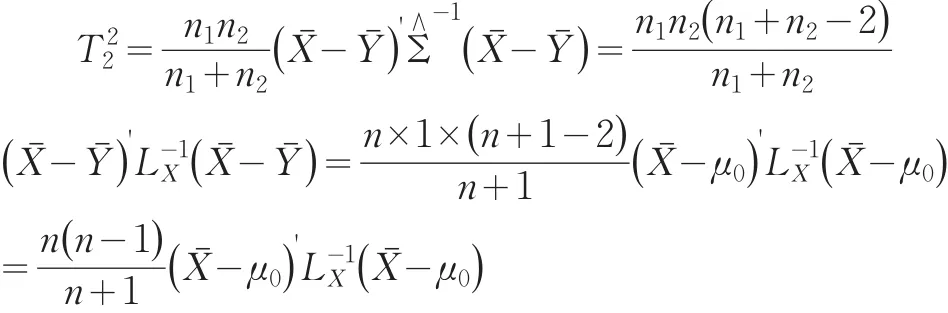
即：

比较（1）、（7）两式，可得：

由于在两总体均值的比较的假设检验中，有：

由（8）、（9）两式及 n1=n, n2=1的假设前提，有：

将（10）代入（8）式得：

将（11）式代入（2）式得：

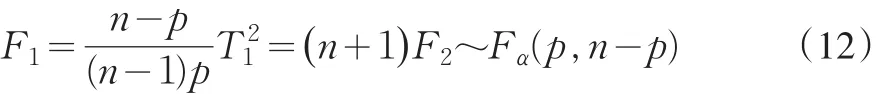
由于F2的值是可以把对均值向量的检验视作两总体均值比较的问题时而通过运行SPSS得到，进而通过（12）式求得F1，于是，均值向量的假设检验问题便可迎刃而解了。

2 利用新方法的多元均值检验

[例]【4】人的出汗多少与人体内钠和钾的含量有一定的关系，今测了20名健康成年女性的出汗多少（x1）、钠的含量（x2）和钾的含量（x3），其数据列于表1，假定x=(x1,x2,x3)'服从三元正态分布。试在显著性水平α=0.05下，检验 H0：μ=μ0=(4 ,50,10)'，H1：μ≠μ0

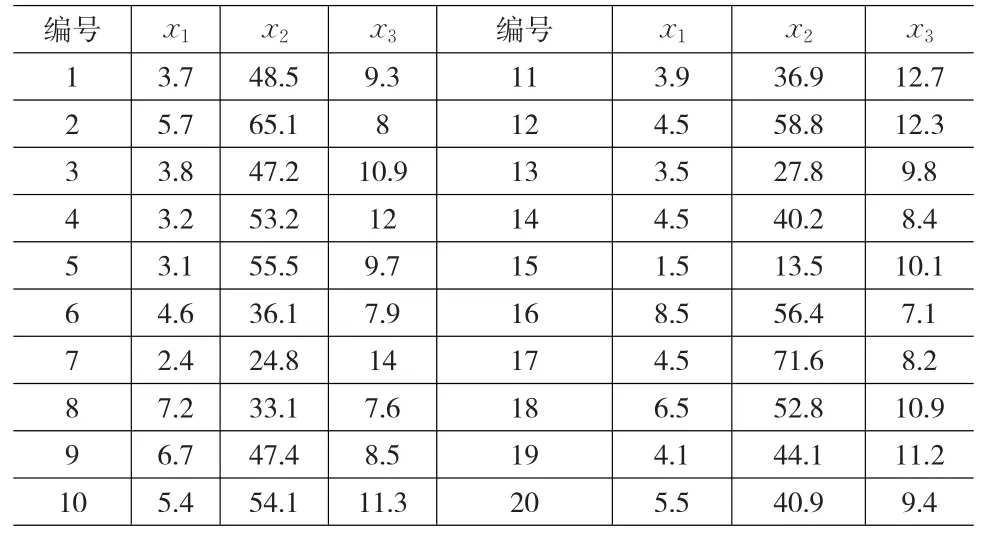
表1 成年女性出汗成分数据

解：将表1的观测数据看作是两总体均值比较检验的样本X，即设n1=20，对应的群组变量值设为1；设全国平均值 μ0=(1 7.5, 27.5, 5, 35)'为样本 Y ，即 n2=1 ，且对应的群组变量值设为2。然后，如文[1]那样，在SPSS17.0中点击“ Analyze→General Linear Model→Multivariate”，将x1、x2、x3选入“Dependent variebles”，将group选入“fixed factor(s)”中，点击OK即可得到输出结果（表2）。