时间偏好动态不一致与社会养老保险研究
2012-09-26刘建颖
刘建颖
0 引言
公共养老保障具有三个主要功能:首先,它是一种强迫个体进行储蓄的承诺机制;其次,它实现了老年人之间的收入再分配;再次,它确保了个体能抵御健康和死亡风险。对退休行为的研究是伴随着现代社会保障体系的建立开始的。退休从本质上看,就是个体永久地退出劳动力市场。它可分为自愿退休与非自愿退休两种情况。对于个体而言,自愿退出劳动力市场总是一个可行的选择。
本文将详细分析存在社会养老保险时,时间偏好动态不一致情形下,退休年龄内生时的两期模型。笔者期望通过将时间偏好动态不一致性引入对社会养老保险的分析,重新考察个体跨期决策中退休行为的决定,试图得到个体跨期决策的时间不一致性是能够解释观察到的退休行为的异常性的;引入时间偏好的动态不一致可能有助于对政府未来的改革政策的有效性进行相关预测。
1 模型的基本假设
我们在Cremer和Pestieau(2003)关于退休年龄内生时的两期模型的分析框架下引入时间偏好动态不一致,期望对时间偏好动态不一致情形下,养老保险制度如何影响经济中真实的宏观经济变量有所认识。
假设时间偏好的动态不一致不仅在代际间存在,在代际内也存在。假设偏好为拟双曲贴现偏好。根据Frederick et al.(2002),将具有时间不一致性的个体区分为两种类型:老练型个体和天真型个体。
假设每个人都存在着“自我控制”问题,用β表示,但当事人意识到的“自我控制问题”的程度为,即个体认为自身在将来会遇到“自我控制问题”的程度为。这两种类型的个体在进行效用最大化选择时,情形如下:
(1)老练型个体,能完全意识到自身存在“自我控制”问题,并能准确地预测自己将来的行为。有β=β̂<1。
(2)天真型个体,完全不能意识到自身存在的“自我控制”问题,因而会错误地预测将来的行为;有β<β̂=1。
假设个体生活两期:年轻期和年老期。两期的长度均标准化为1。年轻时,也就是第一期,个体的劳动供给是无弹性的。年老时,也就是第二期,劳动供给内生决定。这是一个具有内生劳动供给和内生退休年龄的跨期消费模型。
假设个体的劳动生产率ω是随机的,其累积分布函数为F(⋅),密度函数为 f(⋅)。养老保险体系一般通过征收收入税的形式来平衡预算。我们假设第一期工资税税率为θ,第二期养老保险税税率为θ′,其中θ,θ′∈( )0,1。年轻时(第一期),个体决定储蓄的数量s,s仅能在退休后才能获得收益。定义r为外生利率水平。假设人口增长率为n,它是外生给定的。记Lt-1为t期时的老年人,Lt为t期时的年轻人,且Lt=Lt-1⋅(1+n)。年老时(第二期),个体决定最优退休年龄。假设γ为第二期时的工作长度,其中γ∈( )0,1,则1-γ为退休期长度。由于第二期的长度已标准化为1,我们在下文中为叙述方便起见,不妨也称γ为最优退休时刻(或最优退休年龄)。
年轻期(第一期),个体的劳动生产率为ω,工作时间为1,所以其工资收入为ω,缴纳工资税ωθ,税后工资收入一部分用来储蓄,一部分用来消费。
年老期(第二期),个体的劳动生产率为ω,工作时间为γ,所以其工资收入为ωγ,缴纳养老保险税ωγθ′,则第二期的税后收入为ωγ(1-θ′)。年老时(第二期),个体在年轻期(第一期)的储蓄收入变为s(1+r),个体退休后获得养老金收益b。同时假设个体在年老时(第二期)因工作时长γ会有一(用货币度量的)负效用--gγ(其中A>0,g>0)。它表明年老时(第二期)工作时间γ越长,损失的效用越大。假设个体退休后会从休闲中获得正效用+h(1-γ)(其中 B>0,h>0),它表明退休期长度(1-γ)越大,从休闲中获得的正效用越大。
假设个体在年轻期(第一期)和年老期(第二期)的消费水平分别为c1和c2,个体的跨期效用函数为U=u(c1)+βδ⋅u(c2),其中β代表时间偏好不一致的短期贴现因子,δ代表时间一致的长期贴现因子(β>0,δ>0)。这表明个体在代际间存在着时间偏好的动态不一致性。假设u为即期效用函数,对所有个体均一样,它是递增的凹函数,满足古典的Inada条件。
于是个体在年轻期(第一期)时的消费水平为c1=ω(1-θ)-s,在年老期(第二期)时的消费水平为ωγ(1-θ′)+s(1+r)+b ,个体在第二 期的 效用 水平 为
假设养老金收益函数为
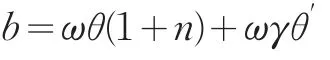
养老金收益b必须在个体退休后才支付。也就是说,个体必须真实地完全退出劳动力市场后,才能获得养老金收益b。由=ωθ′>0可看出,退休后获得的养老金收益b与退休时刻γ正相关。即个体工作时间越长,退休后获得的养老金收益越多;个体工作时间越短,退休后获得的养老金收益也相应变少。在第3节中,个体退休后获得的养老金b与退休时刻γ无关;但在本节中,我们引入了时间偏好的动态不一致,个体退休后获得的养老金收益b与退休时刻γ正相关。
2 最优退休年龄
年轻期(第一期),个体的最优化问题为
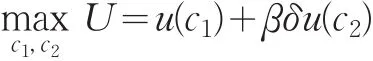
其中:
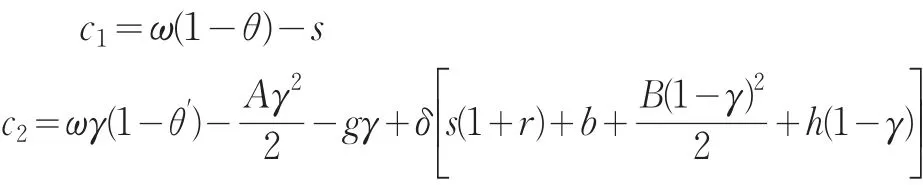
于是个体在第一期时通过选择最优储蓄量s,最大化如下目标函数:

年老期(第二期),个体在代际内存在着时间偏好的动态不一致性。老年个体面临着如下权衡取舍关系:一方面,现在若继续工作,则能在未来获得更多养老金,但同时也会有一工作时的负效用--gγ ;另一方面,若现在立即退休,则可以享受更多的闲暇,获得正效用但其退休后获得的养老金收益b也会减少。
个体在代际内存在的时间偏好动态不一致性使得个体对工作期赋予更多的权重;老年个体在评估上述权衡取舍关系中后者时,使用了贴现因子βδ。
个体在年老期(第二期)时,通过选择最优退休时刻γ*来最大化第二期消费。个体在年轻期(第一期)做优化问题时,考虑到退休时刻γ由第二期决定,γ=γ*;选择最优储蓄水平s最大化第一期的目标函数。
下面我们先来求解第二期的最优化问题。年老期(第二期),个体的最优化问题为

个体通过选择最优退休时刻γ,最大化上述目标函数。
将b=ωθ(1+n)+ωγθ′代入目标函数,得到

关于γ的一阶条件为:

可求得
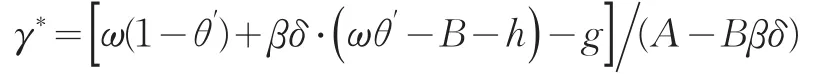
假设内点解条件满足,如A-Bβδ>0。
由比较静态分析,易知
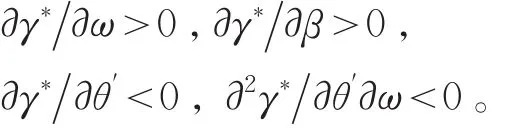
下面我们通过解释相应的经济学含义,可以看到引入时间偏好的动态不一致性后,影响个体最优退休时刻γ*的相关因素。
由∂γ*∂ω>0可知,最优退休时刻γ*是关于个体劳动生产率ω的增函数。即个体的劳动生产率ω越高(工资水平越高),他会选择工作更长时间并更晚退休。因此工资水平高的个体相对于工资水平低的个体会工作更长时间,更晚退休。从经济学直觉上理解,对于相对富裕的个体而言,其第二期的消费——休闲的相对价格要低一些,因此会比相对贫穷的个体更加努力工作并更晚退休。由∂γ*∂β>0可知,时间不一致性贴现因子β越大,最优退休时刻γ*也越大。在时间偏好动态不一致情形下,0<β<1表示时间偏好动态不一致的个体对当前期赋予更大的权重,其偏好类型是当前偏好型的。β越大,表示个体对未来越看重,此时最优退休时刻γ*也越大,个体越倾向于更晚退休;β越小,表示个体对当前期越看重,此时最优退休时刻γ*也越小,个体越倾向于提前退休。
老练型个体,能完全意识到自身存在的时间偏好动态不一致性问题,并能准确地预测自己将来的行为。有β=β̂<1。老练型个体真实的退休时刻为 γ(β ),预测的退休时刻为 γ(β̂);由 β=β̂知,γ(β)=γ(β̂)=γ*,老练型个体能正确预测其真实退休时刻;
天真型个体,完全不能意识到自身存在的时间偏好动态不一致性问题,因而会错误地预测将来的行为;有β<β̂=1。天真型个体真实的退休时刻为 γ(β ),预测的退 休 时 刻 为 γ(β̂);由 β<β̂及 ∂γ*∂β >0 可 知 ,γ*=γ(β)<γ(β̂),因此天真型个体会高估其真实退休时刻。由∂γ*∂θ′<0可知,最优退休时刻γ*是关于养老保险税税率θ′的减函数。即养老保险税税率θ′越高,个体越倾向于提前退休。
由 ∂2γ*∂θ′∂ω<0 可知,个体的劳动生产率 ω 越高(工资水平越高),养老保险税税率θ′对最优退休年龄γ*的影响更显著。
进一步地,我们有如下定理。
定理1在时间偏好动态不一致的两期模型中,老练型个体和天真型个体都会提前退休(即提前退出劳动力市场)。
证明:老练型个体,能完全意识到自身存在的时间偏好动态不一致性问题,并能准确地预测自己将来的行为。有β=β̂<1,其中β为个体真实的时间偏好动态不一致的贴现因子;β̂为其预测的时间偏好动态不一致的贴现因子。于是有即老练型个体真实的退休时刻γ()β和预测的退休时刻γ()是完全一致的。
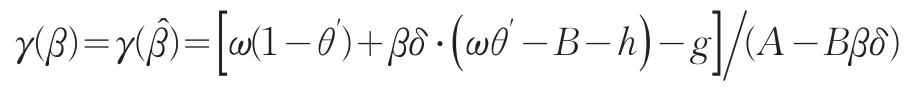
由 ∂γ(β) ∂β >0 可知,γ(β)=γ(β̂)< γ(1)。
这表明时间偏好动态不一致情形下,老练型个体的实际退休年龄要小于时间偏好一致性情形下个体的退休年龄。即老练型个体会提前退休。
天真型个体,完全不能意识到自身存在的时间偏好动态不一致性问题,因而会错误地预测将来的行为。
有β<β̂=1,其中β为个体真实的时间偏好动态不一致的贴现因子;β̂为其预测的时间偏好动态不一致的贴现因子。
天真型个体预测的退休时刻为

=(ω (1-θ′)+δ(ω θ′-B-h)-g ) (A-Bδ)=γ(1)
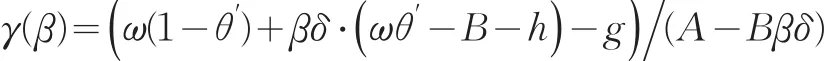
由 ∂γ(β) ∂β >0 可知,γ(β)< γ(β̂)=γ(1)
即天真型个体真实的退休时刻γ()β小于其预测的退休时刻γ()。
天真型个体实际的退休时刻为
这表明时间偏好动态不一致情形下,天真型个体的实际退休年龄要小于时间偏好一致性情形下个体的退休年龄。即天真型个体会提前退休。
综上,时间偏好动态不一致情形下,老练型和天真型个体都会提前退休。
3 养老金收益
定理2在时间偏好动态不一致的两期模型中,老练型个体退休后实际获得的养老金数额等于其预计获得的养老金数额;天真型个体退休后实际获得的养老金数额小于其预计获得的养老金数额。
证明:养老金收益水平为:
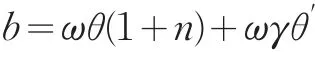
个体实际获得的养老金收益是根据其实际退休年龄来进行支付的,个体预计获得的养老金收益是根据其预计的退休年龄来进行计算的。
4 最优储蓄量
个体在年轻期(第一期)做优化问题时,考虑到退休时刻γ由第二期决定,γ=γ*;选择最优储蓄水平s*来最大化第一期的目标函数。
个体在第一期时的最优化问题为
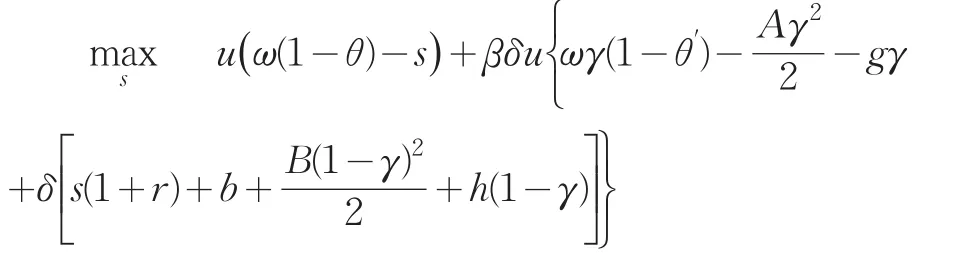
其中
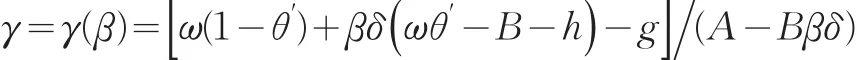
关于s的一阶条件为:
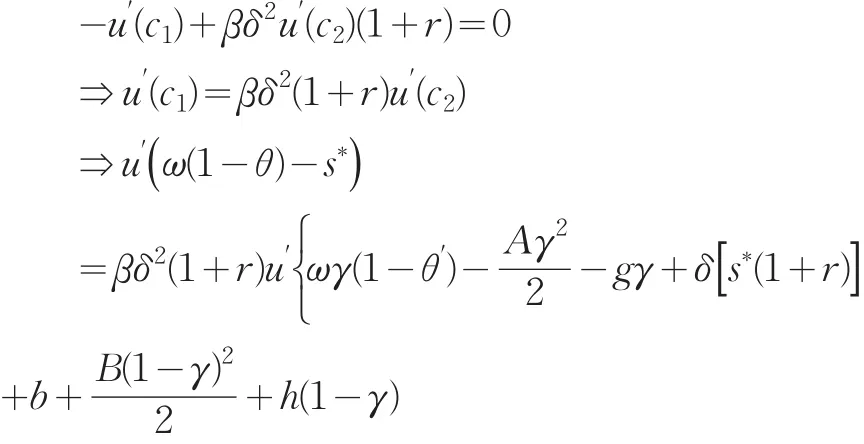
上式意味着,减少一单位工作期消费所造成的效用损失等于增加(1+r)单位退休期消费得到的被βδ2贴现后的效用增加。
将上式对β求导,得到
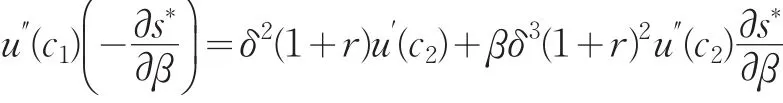
于是有
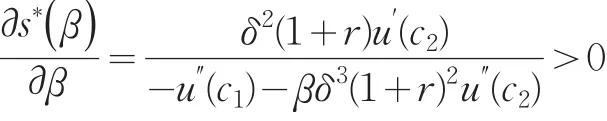
由 u′(c1)=βδ2(1+r)⋅u′(c2)可以看到,若 δ(1+r)=1 成立,则有
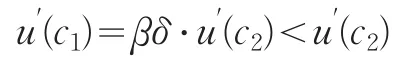
于是c1>c2。
可见,在时间偏好动态不一致情形下,无论是老练型个体,还是天真型个体,他们都不能平滑消费,年轻时会过度消费。我们可以这样来理解:在时间偏好动态不一致情形下,0<β<1表示时间偏好动态不一致的个体对当前期赋予更大的权重,其偏好类型是当前偏好型的。此时个体更看重当期消费,于是年轻期(第一期)会过度消费而储蓄不足。
进一步地,我们有如下定理:
定理3在时间偏好动态不一致性下,经济中的一个帕累托改进是:延长个体的退休年龄或提高其年轻期的储蓄水平。
证明:个体的效用水平为:
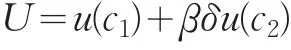
定义:ϕ(β)=U(γ (1))-U(γ ( β))
则有:ϕ(1)=U(γ (1))-U(γ (1))=0
将函数ϕ(β)在β=1的邻域附近泰勒展开,有ϕ′(1)=0,ϕ″(1)> 0 。
于是存在区间(βˉ,1) ,使得该区间内 ϕ(β)>0 。这表明若将个体的真实退休时刻从γ(β)增加到γ(1),其效用水平将会提高。这说明,对经济中个体而言,提前退出劳动力市场并不是一个好的选择。在帕累托意义上,若能延长个体的退休年龄,对其将是一个帕累托改进。
定义:ξ(β)=U(s ( 1))-U(s ( β))
则有:ξ(1)=U(s ( 1))-U(s ( 1))=0
将函数 ξ(β)在 β=1的邻域附近泰勒展开,有 ξ′(1)=0,ξ″(1)> 0 。
5 结论
本文将代际间和代际内的时间偏好动态不一致引入退休年龄内生时的两期模型,得出经济中的老练型个体和天真型个体都会提前退休(即提前退出劳动力市场)。这些结论和现实中观察到的老年人越来越倾向于提早退出劳动力市场也是相符的。战后,绝大多数实行养老保险体系的国家,都出现了老年人口劳动参与率持续下降的现象。老年人越来越倾向于提早退出劳动力市场的现实情况,伴随着老年人口健康状况的改善和预期寿命的提高一同出现,意味着个体越来越倾向于作出提早退休的决策。而伴随着老年人越来越倾向于提早退休的是养老保险体系的不断完善与覆盖面的不断扩大,这意味着二者之间存在着一定的联系。本文从时间偏好动态不一致的角度,分析了养老保险对个体退休决策的影响。
[1]Cremer,H.,Pestieau P.The Double Dividend of Postponing Retire⁃ment[J].International Tax and Public Finance,2003,(10).
[2]Diamond,P.,Koszegi,B.Quasi-Hyperbolic Discounting and Retire⁃ment[J].Journal of Public Economics,2003,(87).
[3]Frederick,S.,Loewenstein,G.,O’Donoghue,T.Time Discounting and Time Preference:A Critical Review[J].Journal of Economic Literature,2002,(40).
[4]Laibson,David Golden Eggs and Hyperbolic Discounting[J].Quarterly Journal of Economics,1997,(112).
