固溶态Cu-Ni-Si合金时效过程的相变动力学

王俊峰，贾淑果,，陈少华，刘 平，宋克兴，刘红勋

(1. 河南科技大学 材料科学与工程学院，洛阳 471003；2. 河南科技大学 河南省有色金属材料科学与加工技术重点实验室，洛阳 471003；3. 中铝洛阳铜业有限公司，洛阳 471039)

固溶态Cu-Ni-Si合金时效过程的相变动力学

王俊峰1，贾淑果1,2，陈少华3，刘 平1，宋克兴1，刘红勋1

(1. 河南科技大学 材料科学与工程学院，洛阳 471003；2. 河南科技大学 河南省有色金属材料科学与加工技术重点实验室，洛阳 471003；3. 中铝洛阳铜业有限公司，洛阳 471039)

通过分析固溶态Cu-Ni-Si合金时效过程中导电率的变化，根据导电率与新相析出量之间的关系计算时效过程中新相的转变比率，在此基础上，确定不同温度下描述时效析出相转变比率与时效时间的Avrami相变动力学经验方程和导电率随时间变化的导电率方程，绘制出动力学“S”曲线，并且用固态热分解反应机理的积分方程验证用Avrami经验方程来描述合金的析出过程的正确性。对Cu-Ni-Si合金在500 ℃时效8 h后的析出相进行选区电子衍射花样标定，发现析出相为δ-Ni2Si和β-Ni3Si。

Cu-Ni-Si合金；时效；转变比率；相变动力学

引线框架是半导体元器件与集成电路封装的主要材料，日本和德国是世界上最大的引线框架铜带出口国，其中以日本产量最大，我国则起步较晚[1−2]。理想的引线框架材料的主要性能指标如下：导电率(IACS)大于80%，抗拉强度大于600 MPa，显微硬度大于180HV[3−4]。作为一种性能优异的时效强化型合金，Cu-Ni-Si系合金因具有高强度、良好的导电性以及低廉的价格，已成为应用前景最为广阔的引线框架材料[5−10]。Cu-Ni-Si系合金在时效过程中，从过饱和固溶体中析出溶质原子Ni和Si，形成新相，新相的含量、形状及分布对合金的性能有很大的影响[11]。而影响该相变的因素很多，要对该相变过程作出完整分析是不可能的。但为了工艺目的，可以用一个单一的Avrami经验方程来描述在恒温下整个转变过程已完成转变部分的比率[12]。由于导电率对析出相的析出非常敏感[13−15]，因此通过导电率的变化对析出相形成的动力学进行研究以得出其Avrami经验方程，对实际生产将具有一定的参考意义。

本文作者通过固溶态Cu-Ni-Si合金时效时导电率的变化计算出新相的转变率，推导出合金在不同温度下的Avrami经验方程和导电率经验方程，根据Avrami经验方程推断出新相的转变机制，并用固态热分解反应机理的积分方程式验证了该合金在400 ℃时效时的转变机制，为该合金的实际生产提供理论依据。

1 实验

试验用Cu-Ni-Si合金的成分(质量分数)如下：2.8%Ni，0.7%Si，0.15%Mg，余量为Cu。合金的生产工艺如下：合金液经过连铸连轧为厚度为20 cm的板材，然后在热轧机上轧制至厚度为15 mm，随后喷水冷却到室温，将试样在900 ℃固溶2 h。将试样分别在400、450和500 ℃时效不同时间(15 min、30 min、1 h、2 h、4 h、6 h、8 h)。

合金的固溶和时效处理在N2保护下的RJX−3−12型管式电阻炉中进行，正常工作时炉温波动±3 ℃，时效时通N2保护并在时效后空冷。导电率试样尺寸为100 mm×3 mm×0.3 mm，电阻测量使用ZY9987型数字式微欧计，合金的导电率是由所测得的电阻值，再根据公式转换而来的，其中L为被测样品的长度，B为被测样品的宽度，H为被测样品的厚度，R为测得的电阻值，导电率值采用国际退火铜标准(%，IACS)。析出相形貌在JEM−2100型高分辨透射电镜上进行观察，电镜试样经电解双喷减出薄区，电解液是HNO3与CH3OH的体积比为1:3的混合溶液，电解液工作温度为−30 ℃。

2 结果与分析

2.1 Cu-Ni-Si合金时效析出相转变比率的测定及计算

由于Cu-Ni-Si合金导电率对相的析出非常敏感,故通过该合金在时效过程中导电率的变化来研究其析出转变过程。当合金时效时，溶质原子自过饱和固溶体中析出形成新相，此时析出相的转变比率φ可定义为

式中：b和n为常数。b取决于温度、原始相的成分和晶粒尺寸等因素；n取决于相变类型和形核位置。求出b和n就可以确定析出相的转变比率与时间的关系，推断析出相的转变机制。合金在一定温度下时效时，导电率随时间的变化为指数关系。而由式(1)可知，φ与t呈指数关系，因此，可以假定合金的导电率σ与析出相转变比率φ有如下线性关系：

当时效刚开始时，新相转变尚未开始，此时φ=0，合金的导电率应为初始导电率为σ0，即固溶后合金的导电率；当导电率达到最大值σmax时，第二相转变结束，此时φ=1。由表1可以看出：当时效时间由6 h至8 h时，导电率变化不大，可以认为这段时间已达到该温度下的σmax。由A=σmax−σ0求出A，再由实验测得的各时刻的导电率(σ)算出相应的析出相转变比率φ(见表1)。

2.2 Cu-Ni-Si合金的相变动力学方程及导电率方程

将式(2)转化为

两边取两次对数可得

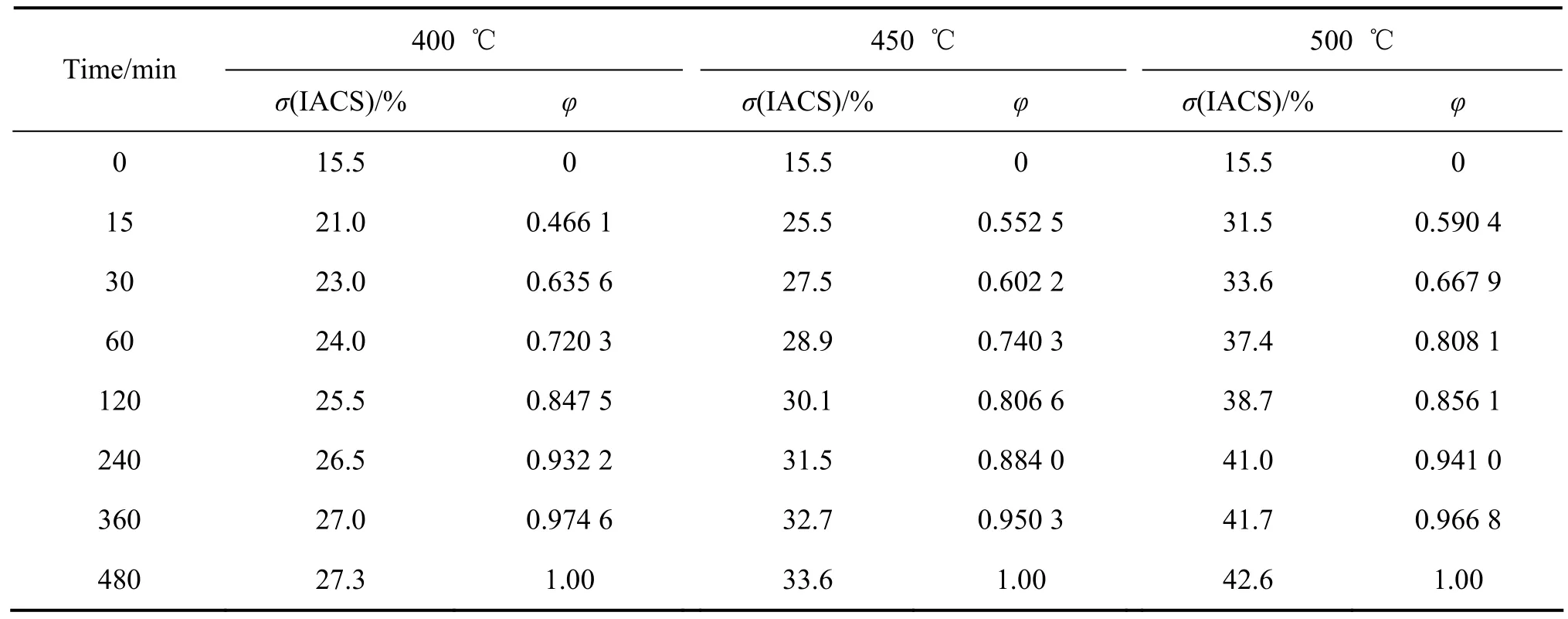
表1 在不同温度下合金的电导率与析出相的转变比率Table 1 Electrical conductivity and transformation ratio of precipitates of alloy aged at different temperatures

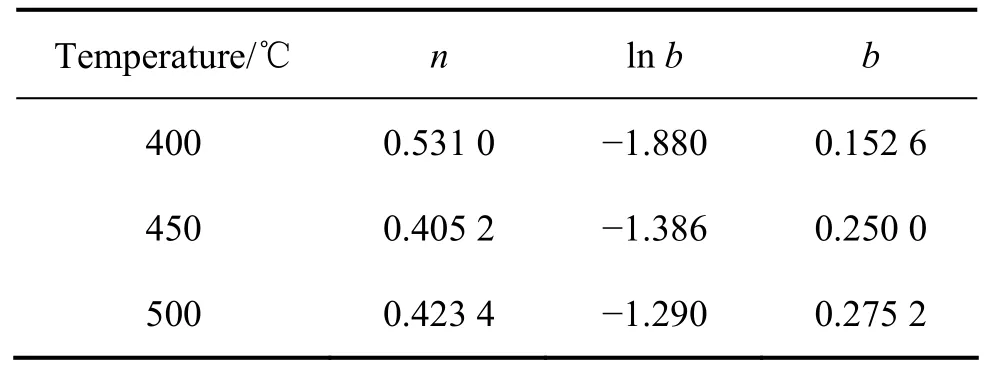
表2 合金在不同温度下的n和b值Table 2 Values ofnandbof alloy at different temperatures

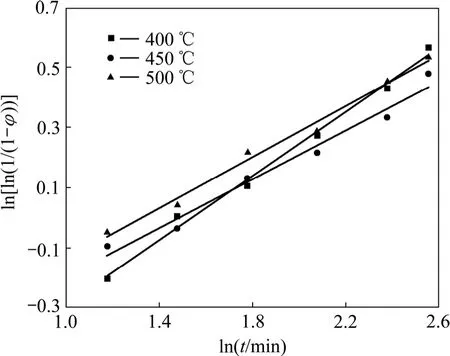
图1 析出相的体积分数与时效时间的对数关系曲线Fig. 1curves of precipitates

将求出的n和b值代入式(2)，可求出固溶态Cu-Ni-Si合金时效的相变动力学方程如下：

400 ℃时，

450 ℃时，

500 ℃时

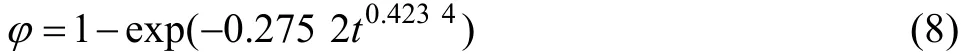
将式(6)、(7)和(8)代入式(2)可得该合金时效时的导电率方程如下：

400 ℃时，

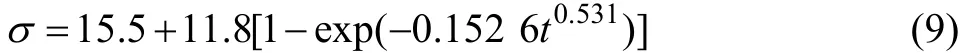
450 ℃时，

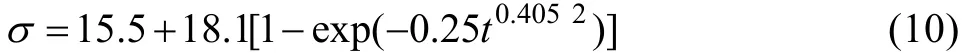
500 ℃时，

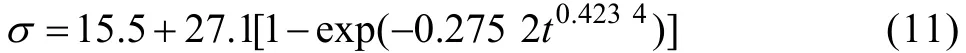
图2所示为由式(6)～(8)作出的该合金在不同时效温度下的相变动力学“S”曲线。从图2可以看出，时效初期转变速度较慢，随时间的延长转变速度增加，在转变末期，转变速度逐渐变缓，并且在时效初期，温度越高，析出新相的体积分数越大，时效1 h后，400 ℃时效的析出相转变比率高于450 ℃时效时的析出相转变比率，这是因为400 ℃时σmax较小，并且在时效时导电率很快就接近σmax，导致在计算转变比率时，时效后期400 ℃的转变比率较高。

2.3 转变机制

固溶态Cu-Ni-Si合金的析出反应方程可看作A(固溶体)→B(固溶体)+C(新相)

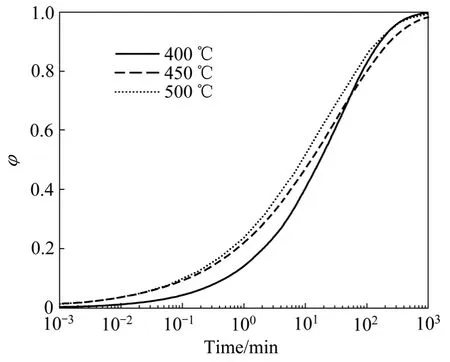
图2 合金在不同温度下的相变动力学曲线Fig. 2 Phase transformation kinetics curves of alloys at different temperatures

固溶体分解速率为

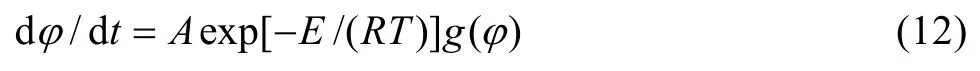
式中：g()φ取决于反应机理；A为Arrhenius方程中的指数前因子；E为析出激活能。对式(12)两边积分，得到下面的方程：

式(12)和式(13)分别是时效析出反应的微分和积分动力学方程。目前常用的积分形式的动力学方程及与之对应的反应机理见表3[16]，表中k=Aexp[−E/(RT)]。

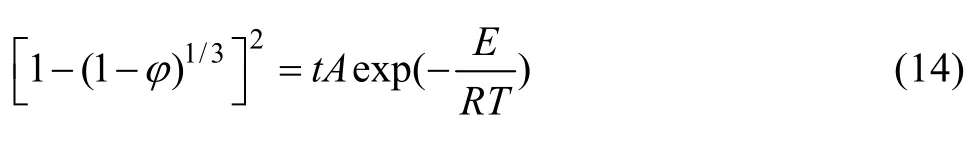
式中：Aexp[−E/(RT)]在400 ℃时可以看作常数，设为a。对式(14)两边同时取对数得：

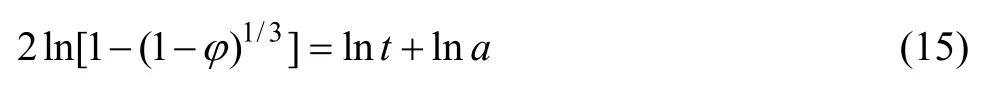
表3 积分形式的动力学函数及反应机理与n的对应关系[16]Table 3 Relation among integral kinetics functions, corresponding reactive mechanisms andn[16]

利用表1中400 ℃时效时的时间t和转变比率φ作出2ln[1−(1−φ)1/3]与lnt的关系图，如图3所示，通过拟合得出其斜率为0.86，与1很接近，再一次验证了Cu-Ni-Si合金在400 ℃时效时的反应机理为受三维扩散控制的反应机理。

由表2可知：固溶态Cu-Ni-Si合金在400～500 ℃时效时n值在0.4至0.53之间，排除误差的影响，可以认为n值与0.53相近，故可以认为固溶态Cu-Ni-Si合金在时效时的反应机理为受三维扩散控制的反应机理，这说明用Avrami经验方程可以很好地描述合金的析出过程。

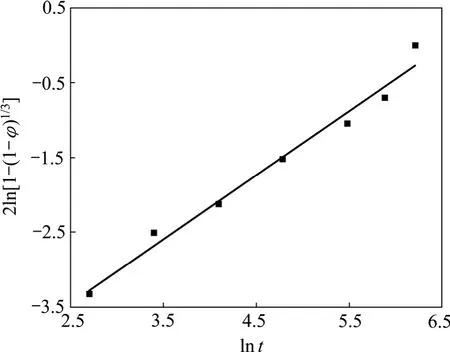
图3 合金在400 ℃时效时2ln[1−(1−φ)1/3]和lnt的关系曲线Fig.3 2ln[1−(1−φ)1/3]—lntdiagram of alloy aged at 400 ℃

2.4 析出相结构

图4所示为Cu-Ni-Si合金在500 ℃时效8 h的显微组织。从图4(a)可以看出析出相呈弥散分布，从图4(b)可以看出析出相呈圆盘状(白色箭头所指)，这与合金受三维扩散控制的反应机理的分析一致。通过对合金的析出相进行选区电子衍射分析，并对其进行标定(见图4(d))，发现析出相为δ-Ni2Si和β-Ni3Si。

图4 Cu-Ni-Si合金在500 ℃时效8 h析出相的形貌及电子衍射花样标定Fig.4 Morphologies and its indexing of diffraction patterns of precipitates of Cu-Ni-Si alloy: (a), (b) Bright-field images; (c) Selected area diffraction pattern of precipitate in Fig.4(b); (d) Schematic diagram of selected area diffraction pattern

3 结论

1) 固溶态Cu-Ni-Si合金时效过程中导电率的增加量与析出相存在线性关系，合金相变过程可以通过时效过程中导电率的变化反映出来。

2) 通过导电率的变化推导出固溶态Cu-Ni-Si合金在试验温度下的相变动力学方程和导电率方程，该合金在450 ℃时效时的相变动力学方程和导电率方程分别为φ=1−exp(−0.25t0.4052)和σ=15.5+18.1× [1−exp(−0.25t0.4052)]。

3) 固溶态Cu-Ni-Si合金在400～500 ℃时效时受三维扩散机理控制，Avrami经验方程能够正确描述合金的析出过程。

4) Cu-Ni-Si合金在500 ℃时效8 h后的析出相为δ-Ni2Si和β-Ni3Si。

REFERENCES

[1]张 毅, 刘 平, 田保红, 贾淑果, 范 丽. Cu-Ni-Si合金冷变形及动态再结晶行为研究[J]. 功能材料, 2010, 41(3): 446−449. ZHANG Yi, LIU Ping, TIAN Bao-hong, JIA Shu-guo, FAN Li. Study on cold deformation and dynamic recrystallization behavior of Cu-Ni-Si alloy[J]. Journal of Functional Materials, 2010, 41(3): 446−449.

[2]张 毅, 刘 平, 田保红, 陈小红, 贾淑果, 任凤章, 龙永强.时效对Cu-3.2Ni-0.75Si-0.30Zn合金组织和性能的影响[J]. 功能材料, 2007, 38(6): 908−910. ZHANG Yi, LIU Ping, TIAN Bao-hong, CHEN Xiao-hong, JIA Shu-guo, REN Feng-zhang, LONG Yong-qiang. Effect of agingon microstructure and properties of Cu-3.2Ni-0.75Si-0.3Zn alloy[J]. Journal of Functional Materials, 2007, 38(6): 908−910.

[3]雷静果, 刘 平, 赵冬梅, 康布熙, 田保红. 用导电率研究Cu-Ni-Si-Cr合金时效早期相变动力学[J]. 材料热处理学报, 2003, 24(4): 22−26. LEI Jing-guo, LIU Ping, ZHAO Dong-mei, KANG Bu-xi, TIAN Bao-hong. Study on the transformation kinetics of early stage aging of Cu-Ni-Si-Cr alloy by measuring the electric conductivity[J]. Transactions of Materials and Heat Treatment, 2003, 24(4): 22−26.

[4]龙永强, 刘 平, 刘 勇, 张伟民. 高性能Cu-Ni-Si合金材料的研究进展[J]. 材料导报, 2008, 22(3): 48−51. LONG Yong-qiang, LIU Ping, LIU Yong, ZHANG Wei-min. Progress in research on high performance Cu-Ni-Si alloys[J]. Materials Review, 2008, 22(3): 48−51.

[5]HUANG Fu-xiang, MA Ju-sheng, NING Hong-long, CAO Yun-wen, GENG Zhi-ting. Precipitation in Cu-Ni-Si-Zn alloy for lead frame[J]. Materials Letters, 2003, 57: 2135−2139.

[6]SU Juan-hua, LI He-jun, DONG Qi-ming, LIU Ping, KANG Bu-xi. Prediction and analysis of the aging properties of rapidly solidified Cu-Cr-Sn-Zn alloy through neural network[J]. Journal of Materials Engineering and Performance, 2005, 14(3): 363−366.

[7]SUN Z, LAITEM C, VINCENT A. Dynamic embrittlement at intermediate temperature in a Cu-Ni-Si alloy[J]. Materials Science and Engineering A, 2008, 447(1/2): 145−152.

[8]张凌峰, 刘 平, 康布熙, 赵冬梅, 田保红, 董企铭. Cu-3.2Ni-0.75Si-0.30Zn合金时效过程的动力学分析[J]. 中国有色金属学报, 2003, 13(3): 717−721. ZHANG Ling-feng, LIU Ping, KANG Bu-xi, ZHAO Dong-mei, TIAN Bao-hong, DONG Qi-ming. Kinetics of aging process of Cu-3.2Ni-0.75Si-0.30Zn alloy[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(3): 717−721.

[9]李 伟, 刘 平, 马凤仓, 刘心宽, 陈小红, 张 毅. 时效与冷变形对 Cu-Ni-Si 合金微观组织和性能的影响[J]. 稀有金属, 2011, 25(3): 330−335. LI Wei, LIU Ping, MA Feng-cang, LIU Xin-kuan, CHEN Xiao-hong, ZHANG Yi. Effects of aging and cold deformation on microstructure and properties for Cu-Ni-Si alloy[J]. Chinese Journal of Rare Metals, 2011, 25(3): 330−335.

[10]SU Juan-hua, DONG Qi-ming, LIU Ping, LI He-jun, KANG Bu-xi. Research on aging precipitation in a Cu-Cr-Zr-Mg alloy[J]. Materials Science and Engineering A, 2005, 392(1/2): 422−426.

[11]陈 健, 刘雪飘, 梁 欢. 铜镍钴铍合金的时效相变动力学方程[J]. 机械工程材料, 2011, 35(1): 19−21. CHEN Jian, LIU Xue-piao, LIANG Huan. Aging transformation kinetic equation of CuNiCoBe alloy[J]. Materials for Mechanical Engineering, 2011, 35(1): 19−21.

[12]盖伊A G, 赫仑J J. 物理冶金学原理[M]. 北京: 机械工业出版社, 1981: 259−291. GUY A G, HREN J J. Elements of physical metallurgy[M]. Beijing: China Machine Press, 1981: 259−291.

[13]董琦袆. 低浓度Cu-Ni-Si合金的组织及性能研究[D]. 长沙:中南大学, 2010. DONG Qi-yi. Study on microstructure and property of the low concentration Cu-Ni-Si alloy[D]. Changsha: Central South University, 2010.

[14]黄金亮, 叶权华, 刘 平, 刘 勇，田保红. 用导电率研究Cu-Cr-Zr-Y合金的相变动力学[J]. 材料热处理学报, 2006, 27(2): 132−136. HUANG Jin-liang, YE Quan-hua, LIU Pin, LIU Yong, TIAN Bao-hong. Study on kinetics of phase transformation of Cu-Cr-Zr-Y alloy though measurement of electric conductivity[J]. Transactions of Materials and Heat Treatment, 2006, 27(2): 132−136.

[15]曹育文, 马营生, 唐祥云, 王碧文, 王世民, 李 红. Cu-Ni-Si系引线框架用铜合金成分设计[J]. 中国有色金属学报, 1999, 9(4): 723−727. CAO Yu-wen, MA Ying-sheng, TANG Xiang-yun, WANG Bi-wen, WANG Shi-min, LI hong. Design of Cu-Ni-Si copper alloy for lead frame[J]. The Chinese Journal of Nonferrous Metals, 1999, 19(4): 723−727.

[16]陈镜泓, 李传儒. 热分析及其应用[M]. 北京: 科学出版社, 1985: 112−135. CHEN Jing-hong, LI Chuan-ru. Thermal analysis and application[M]. Beijing: Science Press, 1985: 112−135.

(编辑 龙怀中)

Kinetics of phase transformation of solution-treated Cu-Ni-Si alloy during aging treatment

WANG Jun-feng1, JIA Shu-guo1,2, CHEN Shao-hua3, LIU Ping1, SONG Ke-xing1, LIU Hong-xun1
(1. School of Materials Science and Engineering, Henan University of Science and Technology, Luoyang 471003, China; 2. Henan Key Laboratory of Advanced Non-Ferrous Materials, Henan University of Science and Technology, Luoyang 471003, China; 3. CHINALCO Luoyang Copper Co., Ltd., Luoyang 471039, China)

The transformation ratio of new phase in Cu-Ni-Si alloy was calculated in terms of analyzing the electrical conductivity variations and the relationship between the electrical conductivity and the quantity of new phase. Both the Avrami phase transformation kinetics equation and the electrical conductivity equation changing with the aging time were derived at different temperatures, the transformation kinetics “S” curve was drawn. Then, though integral functions of the reactive mechanism of thermal decomposition of solid solution, the Avrami formulation for describing the kinetics of the phase transformation is proved to be correct. The precipitates areδ-Ni2Si andβ-Ni3Si phases by indexing the selected field diffraction pattern of precipitates of Cu-Ni-Si alloy aging at 500 ℃ for 8 h.

Cu-Ni-Si alloy; aging; transformation ratio; phase transformation kinetics

TG146.1

A

国家高新技术研究发展计划资助项目(2006AA03Z528)；河南省教育厅科技攻关项目(2009A430007)；河南科技大学科研创新能力培育基金项目(2010CZ0008)

2011-10-14；

2012-05-07

贾淑果，教授，博士；电话：13525410580；E-mail: sgjia@mail.haust.edu.cn

1004-0609(2012)10-2862-06