不锈钢厚板K-PAW三维瞬态温度场的数值模拟

李瑞英

(大庆师范学院 物理与电气信息工程学院，黑龙江 大庆 163712)

0 引言

小孔等离子弧焊接(K-PAW)是适合于中厚板的高效焊接工艺，在设备造价、维护费用、操作复杂度及焊枪灵活度等方面都具有较强的优势[1]。焊接热过程对小孔的形成起着决定性作用，等离子弧焊接温度场的数值分析，能够为K-PAW参数优化及其焊接过程自动化的实现提供理论依据，具有重要的意义[2]。由于K-PAW焊接过程的复杂性，目前关于K-PAW焊接过程数值模拟的研究尚少见报道，一些研究者利用平面Guass热源描述K-PAW的焊接热输入[3-5]，不是很符合K-PAW焊接的实际情况。只有考虑等离子弧热流沿焊件厚度方向的体积分布和等离子弧沿焊板厚度(熔池深度)方向上的“挖掘”作用等因素，对K-PAW焊接过程的数值模拟时才会比较准确。

采用复合三维锥体热源模式，建立了运动电弧作用下的K-PAW焊接热过程的数值模型，间接考虑相变潜热和流场的作用，预测其焊接9.5 mm不锈钢0Cr18Ni9厚板时三维瞬态焊接温度场的动态演变。

1 温度场数学模型

运动电弧作用下的小孔等离子弧焊接过程包括熔化、热传导、辐射、对流、蒸发和凝固等诸多复杂的物理化学变化过程，如图1所示[6]。

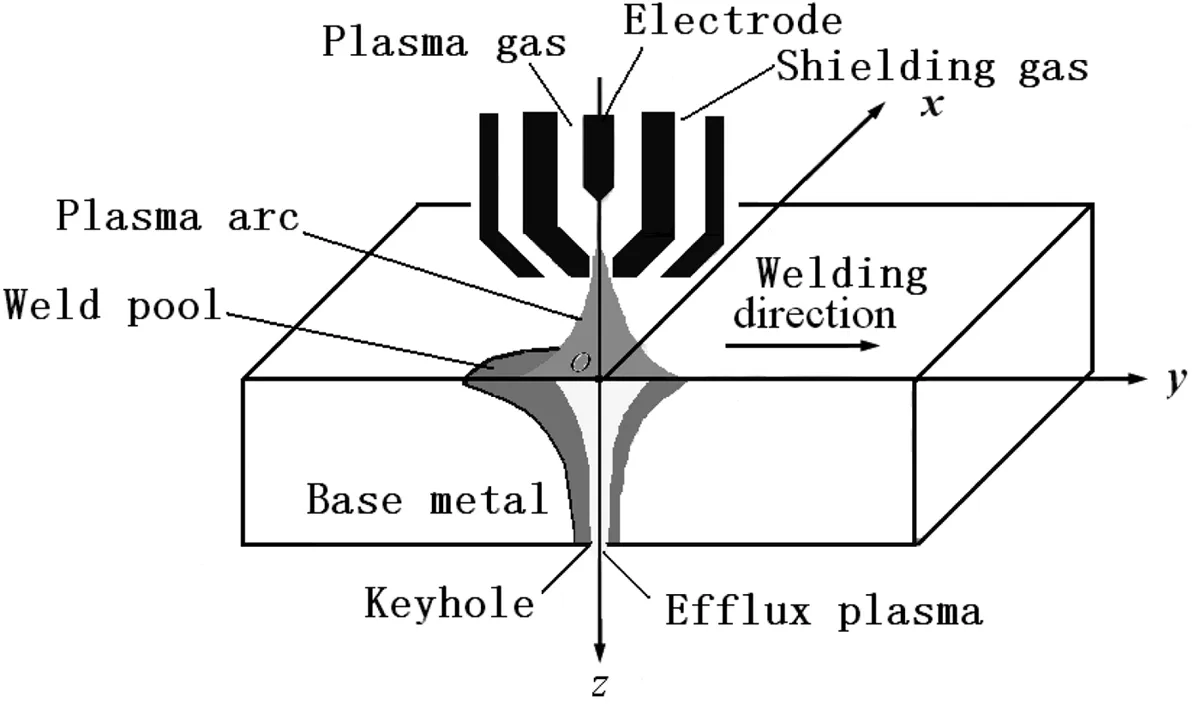
图1 K-PAW示意图[6]

1.1 控制方程

移动坐标系(x,y,z)下，各向同性、无体内热源物体中控制温度分布和热流传导的热传导方程为：

(1)

式中：x，y，z是移动坐标系；T(x,y,z,t)是位置坐标(x,y,z)与时间t的函数；ρ是工件密度；Cp是比热容；v0是焊接速度；T是温度；t是焊接时间；k是热导率；Q是热源项，间接考虑相变时为相变潜热。

1.2 边界条件

1.2.1 初始条件

起弧时，能量守恒方程的初始条件为

t= 0 ，T(x,y,z, 0 )=Ta

(2)

式中：Ta为环境温度。

1.2.2 边界条件

在焊件的上表面边界条件为

-k

(3)

(4)

Qevp=mevpLe

(5)

Qc=ac(T-Ta)

(6)

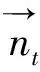
下表面边界条件为

-k

(7)

Qc=ac(T-Ta)

(8)

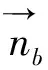
侧面(x= 焊件的半宽)为

(9)

两个端面(即沿y方向的两个端面)为

(10)

对于焊件对称面(x= 0)，绝热边界条件为

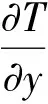
(11)

1.3 复合三维椎体热源模型

小孔等离子弧焊接热源沿厚度方向分布的特点决定了平面热源作用模式不符合实际。小孔等离子弧焊接过程中，等离子流的作用力很大，对熔池形状及小孔形状具有决定性的作用[2]，考虑到轴向热传导，采用实质是一系列平面高斯热源沿焊件厚度z方向叠加而成的复合三维锥体热源模式(Hybrid three-dimensional conical heat source, HTDC)。

复合三维锥体热源模式是沿z方向(即焊件厚度方向)分布的体积热源模式，在垂直于z轴的各个平面(xoy)内，热流分布半径沿厚度方向呈线性衰减，而焊件厚度方向中心轴(z轴)上，最大热流密度Q0保持不变，如图2所示。复合三维锥体热源模型的数学表达式为：

(12)

(13)

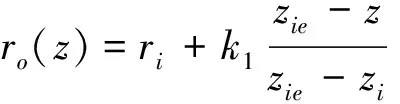
(14)

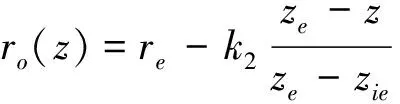
(15)

式中：δQo是热流密度分布参数；r是热流作用区域的半径；xo，yo是热源初始位置；zi是热源作用于焊件下表面的z坐标位置；ze是热源作用于焊件上表面的z坐标位置；zie是热源作用于焊件上、下两部分分界线的z坐标；ri是焊件下表面热流作用区域的半径；re是焊件上表面的热流作用区域的半径；k1，k2是常量。以上参数可通过试验或经验获得。

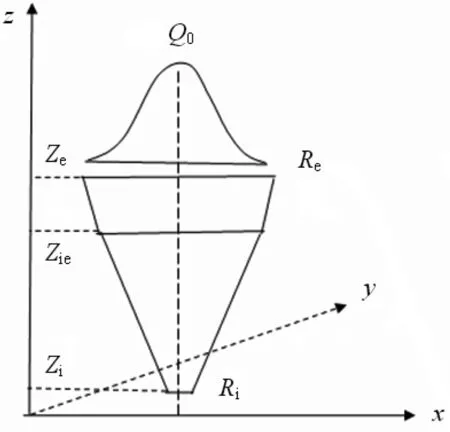
图2 HTDC热源模型图

2 焊接过程物理模型的建立

被焊工件的材料为奥氏体不锈钢0Cr18Ni9，用剪板机将板材剪切成尺寸为200 mm × 80 mm × 9.5 mm的小试件，试样尺寸如图3所示。

数值模拟计算结果的准确性与材料热物性能参数选取的是否准确有着直接的联系。计算中所涉及的热物性参数可分为随温度变化的热物性参数与不随温度变化的热物性参数两大类，其中不随温度变化的热物性参数和被焊工件的化学成分参见文献[7]，而用于材料温度场计算的比热容Cp、综合热传导系数ac、热导率k等热物性参数均是温度的函数，随温度呈非线性变化，如图4所示。

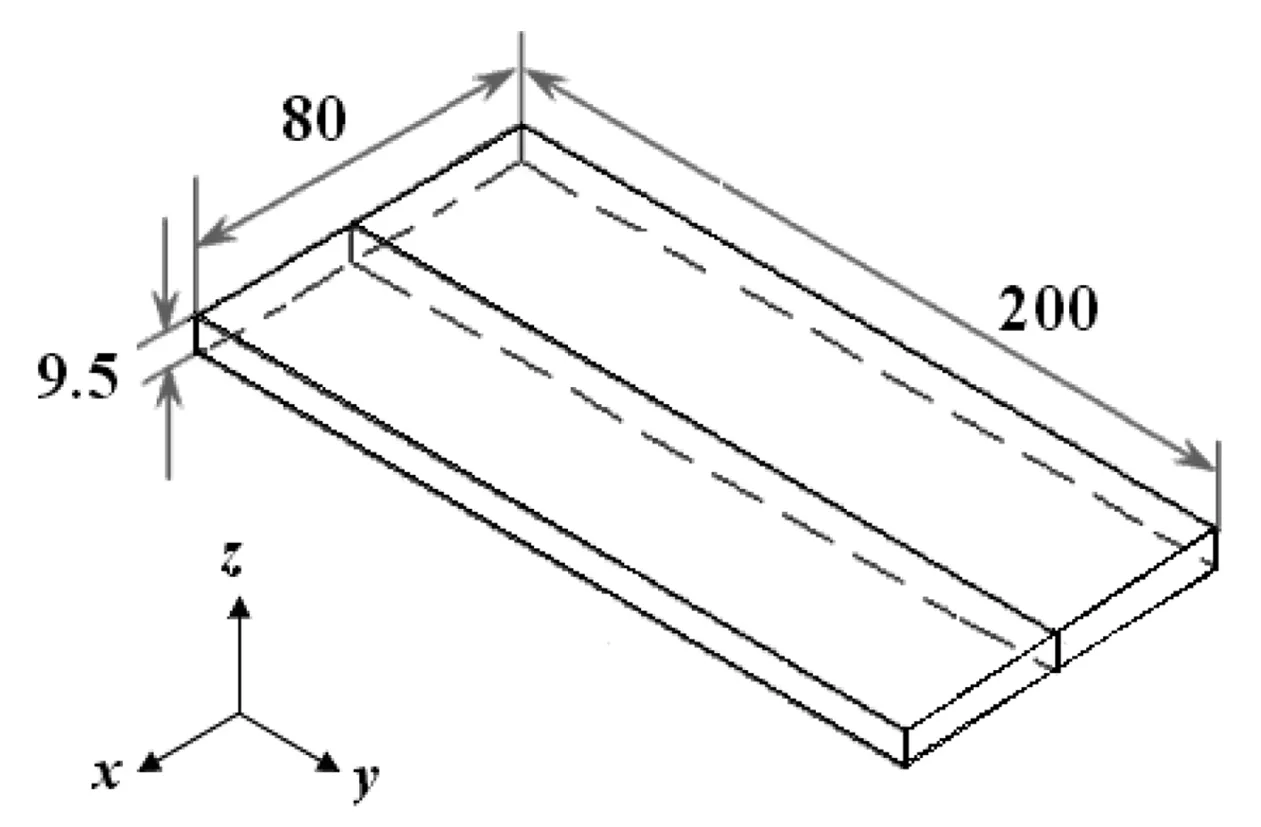
图3 试样尺寸

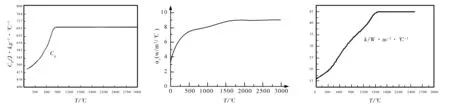
(a) 比热容Cp随温度的变化规律 (b) 综合热传导系数ac随温度的变化规律 (c) 热导率k随温度变化的取值规律

3 数值分析与实验对比

针对具体的K-PAW焊接工艺和条件(9.5 mm厚1Cr18Ni9Ti：I=250A，U=31.7V，V0=2mm/s)，对焊接热源模式进行校正。利用校正所得的HTDC热源模式，综合考虑熔池内部对流散热、熔池表面蒸发散热、熔池固-液界面的相变潜热和材料的热物性参数随温度呈非线性变化等诸多因素，利用计算机语言编程实现。通过数值计算，求解上述定解条件和控制方程。在进行数值模拟计算时，设焊件表面与周围空气的换热系数为25W/(m2·K)。

数值模拟结果表明，引弧后大约经过5s焊接热过程达到宏观准稳态。图5为从开始引弧到达到宏观准稳态这一焊接过程三维温度场的动态演变，焊接温度场的温差间隔为200 K，分别给出了从1s到5s不同时刻，焊件的上表面、横截面、纵截面焊接温度场的动态演变规律。

图5a为固定坐标系下不同时刻焊件上温度场分布。可以看出，在引弧不到1s，焊件上表面的最高温度已达到熔点以上，这是因为K-PAW属于高能量密度焊接，能够瞬间将焊件加热到材料熔点以上的温度。电弧刚刚引燃时，上表面只有一小部分金属熔化，焊件上的温度梯度比较大，熔池周围热影响区的温度比较低。随着焊枪向前推移，焊件上温度升高的速度非常快，等温线迅速向外扩张，等温线的覆盖面积快速变大。3s时焊件上的温度明显升高，高温面积明显变大。之后，焊件后部温度梯度慢慢减小，高温面积逐渐增大。图5b为不同时刻熔深最大处的焊件横截面的温度场分布。随着焊接时间延长，宽度和深度方向等温线的范围均逐渐变大，温度梯度逐渐变小，且温度场的分布沿y轴方向，即焊缝中心线对称。图5c为不同时刻焊件纵截面的焊接温度场的分布情况。随着焊枪向前推移，深度方向等温线的范围均逐渐变大，沿x轴方向，即电弧运动的前后方向焊接温度场的分布不对称，电弧前方的温度梯度变化不大，电弧后方的温度梯度却不断变小。主要由于电弧对焊件前、后方部分的加热时间不同，传热过程不断变化所致。

整个图5表明，在对焊件加热的过程中，焊件上等温线的范围不断扩大，高温面积也逐渐向外扩大。时间为4s和5s时焊件上的焊接温度场分布基本相同，表明5s时K-PAW焊接温度场已达到准稳态。焊件向周围环境散失热量的多少与焊件上的温度分布成正比，焊件温度升高，散失的热量也跟着增多。起弧时，由于焊件上的温度较低，散失的热量就较少，电弧传给焊件的热量大于焊件散失的热量，从而使焊件内部的热量越来越多，焊件的温度越来越高。随着焊枪不断向前推移，焊件上的整体温度不断升高，向周围环境散失的热量也不断增加，散失的热量与电弧传给焊件的热量之差越来越小。当焊件上的温度达到某一特定值时，二者处于平衡状态，即焊件散失的热量等于电弧传给焊件的热量，焊件上的焊接温度场达到宏观准稳态，且随着焊枪的移动同焊接电弧一起向前移动，等温线也随电弧的移动前移。

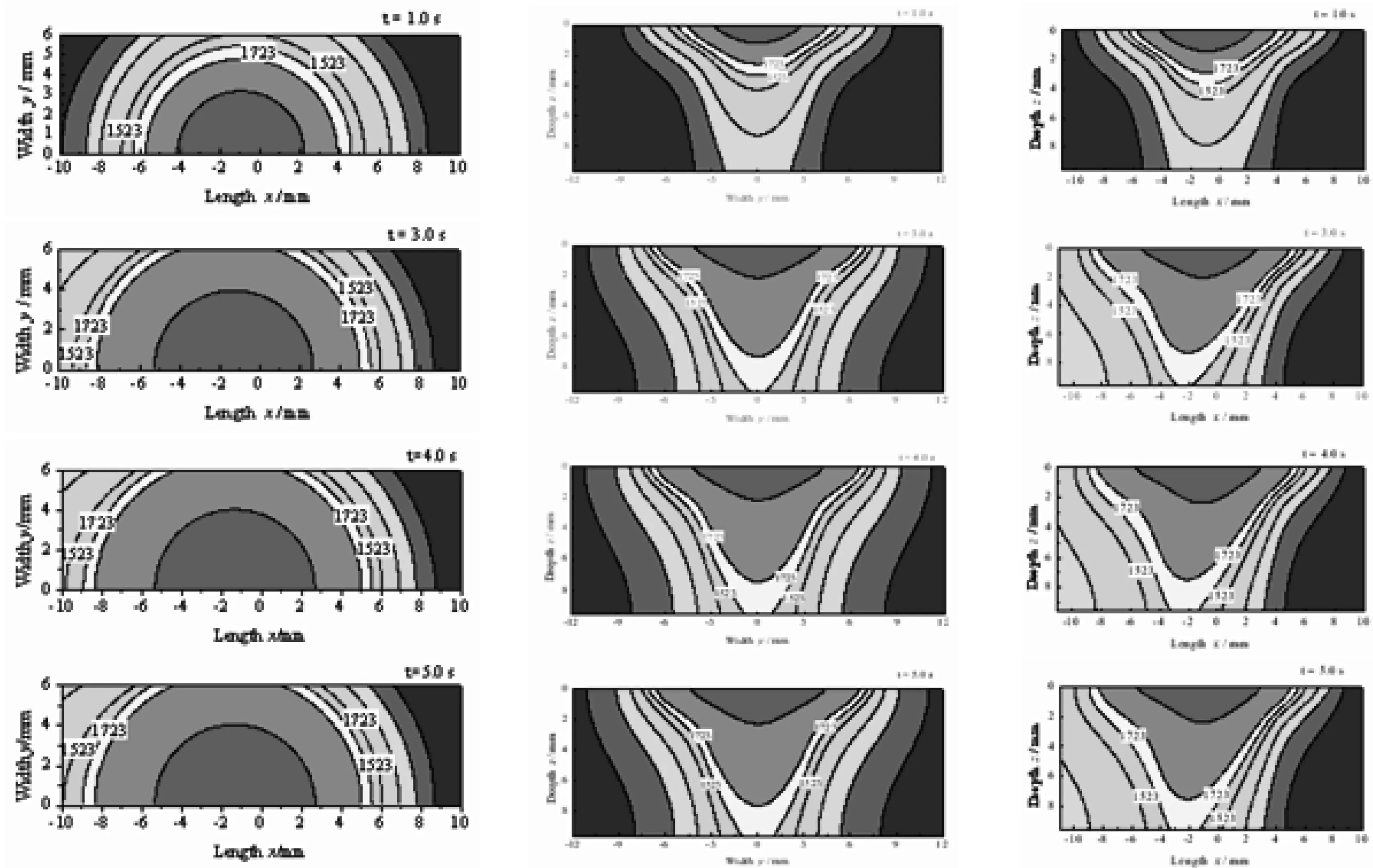
(a) Top surface (b) Cross section (c) Symmetry section

1723 K是不锈钢焊板材料0Cr18Ni9的熔点，通过观察此温度等温线的变化可观察到不同时刻熔池形状的动态演变规律。据此提取熔合线的坐标，并对其进行了实验验证。图6为基于复合三维锥体热源模式的K-PAW焊接9.5 mm不锈钢厚板不同时刻，熔池横截面计算值与实验值的比较。结果表明：在起弧后的一段时间(t< 4.0s)内熔池的上表面熔池宽度和熔池深度计算结果与实验结果有一定差别(这主要是因为计算模型考虑因素与实际焊接环境有一定的差别所导致的)，随着时间的延长，二者的差别逐渐减小，引弧4.0s以后，计算值与实测值基本吻合。对达到准稳态时的焊缝横截面的计算结果进行了实验验证，计算结果与实验结果的比较如图7所示。结果表明：在不考虑表面变形的前提下，上、下表面熔池宽度和熔合线在焊件内的形状与走向，计算值与实测值吻合较好。但达到宏观准稳态之前的熔池基本形状的精度还有待于进一步提高，需在今后工作中继续改进。

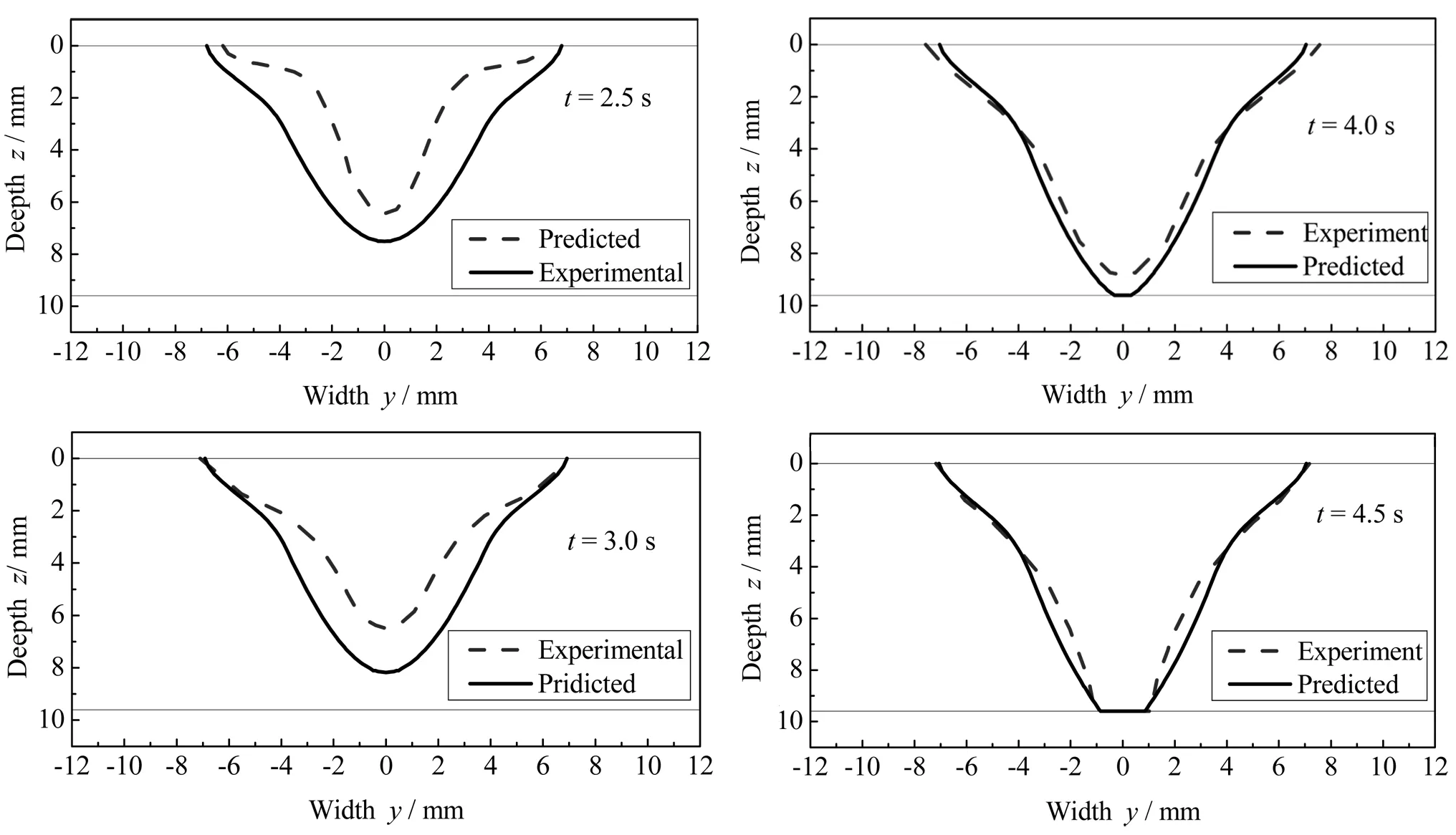
图6 不同时刻熔池横截断面计算值与实验值比较

图7 准稳态时焊缝横截断面计算值与实验值比较

4 结语

1) 通过分析小孔等离子弧焊接工艺的特点，考虑了沿焊件厚度方向的电弧热流密度，建立了适合于K-PAW焊接不锈钢0Cr18Ni9厚板的复合三维锥体热源分布模式和三维动态数值计算模型。

2) 利用所建的热源模型，预测了K-PAW从引弧到达到宏观准稳态过程中焊接温度场和熔池形状的动态演变。结果表明，在不考虑熔池上、下表面变形的前提下，达到宏观准稳态时，焊缝上、下表面熔宽和熔合线在焊件内的形状与走向，计算值与实验值吻合较好，但达到宏观准稳态之前的熔池基本形状的精度还有待于进一步提高。

[参考文献]

[1] 武传松,王怀刚,张明贤.小孔等离子弧焊接热场瞬时演变过程的数值分析[J].金属学报,2006,42(3):310-316.

[2] 王怀刚.三维瞬态小孔等离子弧焊接温度场的数值模拟[D].济南：山东大学硕士学位论文,2005.

[3] 占焕校,王勇,韩涛,等.42CrMo钢表面激光宽带熔凝有限元模拟[J].热加工工艺,2007,36(12): 64-68.

[4] Dong Honggang, Gao Hongming, Wu lin. Numerical simulation of heat transfer based on phoenics during stationary plasma arc welding prosess[J]. Transactions of the Chain Welding Insistution,2002,23(4):24- 36.

[5] 孙俊生,武传松. PAW+TIG电弧双面焊接小孔形成过程的数值模拟[J].金属学报,2003,39(1):79-84.

[6] 李明.等离子焊接气体保护效果数值模拟研究[D].兰州:兰州理工大学硕士学位论文,2007.

[7] 李瑞英.基于SYSWELD的三维瞬态GTAW温度场与应力场的有限元分析[D].东营:中国石油大学(华东)硕士学位论文,2008.