铁电薄膜的介电性质

董云峰，崔 莲

(大庆师范学院 物理与电气信息工程学院，黑龙江 大庆 163712)

0 引言

铁电薄膜一直以来被人们广泛地研究，因为其可以应用于动态随机存取存储器、薄膜传感器、微波设备和红外探测器等[1]。当这些器件的尺寸减小时，表面和尺寸效应对薄膜的应用起了决定性的作用，这主要是由于长程相互作用在铁电材料中起了重要作用。而晶格动力学研究是认识铁电材料性质的本质，因为软模联系于铁电相变。

最近，在实验上，铁电薄膜的晶格动力学已经用不同的技术进行了研究，如红外线椭圆偏光法[3]、太赫时域分光镜[4]和拉曼光谱[5]等。这些研究揭示了铁电薄膜的晶格动力学性质与体材料有着明显的区别。在理论上，据资料所知，仅仅有个别报道铁电薄膜的晶格动力学性质。Wesselinowa[6]应用格林函数技术，在横场Ising模型的框架下，研究了铁电薄膜的动态性质，并指出相对于体材料，铁电薄膜的软模频率变小，而阻尼效应增大。

众所周知，铁电薄膜表面附近的状态与薄膜内部是不同的。由于长程库仑相互作用，许多表面因素，例如间界应力、杂质和电极逐渐影响铁电薄膜的内部结构。Lü和Cao[7]首先引入了表面过渡层来研究这种逐渐过渡的结构对夹持在两金属电极间铁电薄膜静态性质的影响。他们的模型与上述理论模型相比更加实际，因为上述理论模型中存在铁电薄膜的表面到内部结构的突变。至今，含有表面过渡层的铁电薄膜的动态行为未见报道。本文我们将在平均场近似的软模理论框架下，研究含有表面过渡层的铁电薄膜介电函数的实部和虚部随温度变化的动态特性。

1 模型和理论

目前，实际应用的铁电薄膜主要结构是薄膜被夹持在两个平行电极之间，电极可以是金属或者半导体材料。这里假设是金属电极，为理想导体，两个电极被短路，薄膜为绝缘材料。结构模型如图1所示，夹持在两金属电极间含有表面过渡层、厚度为2L的铁电薄膜，在过渡层内体系的性质由表面连续地过渡至薄膜内部。选取薄膜的生长方向为z方向，垂直生长方向的平面为xy平面，将坐标原点取在薄膜中心。由于薄膜很薄，我们假设薄膜是单畴的。铁电薄膜极化方向沿z轴正方向，薄膜表面处极化不连续造成的退极化场完全被金属电极屏蔽，并且在平行于薄膜表面的xy平面内薄膜的性质相同，变化仅仅沿着膜厚方向。

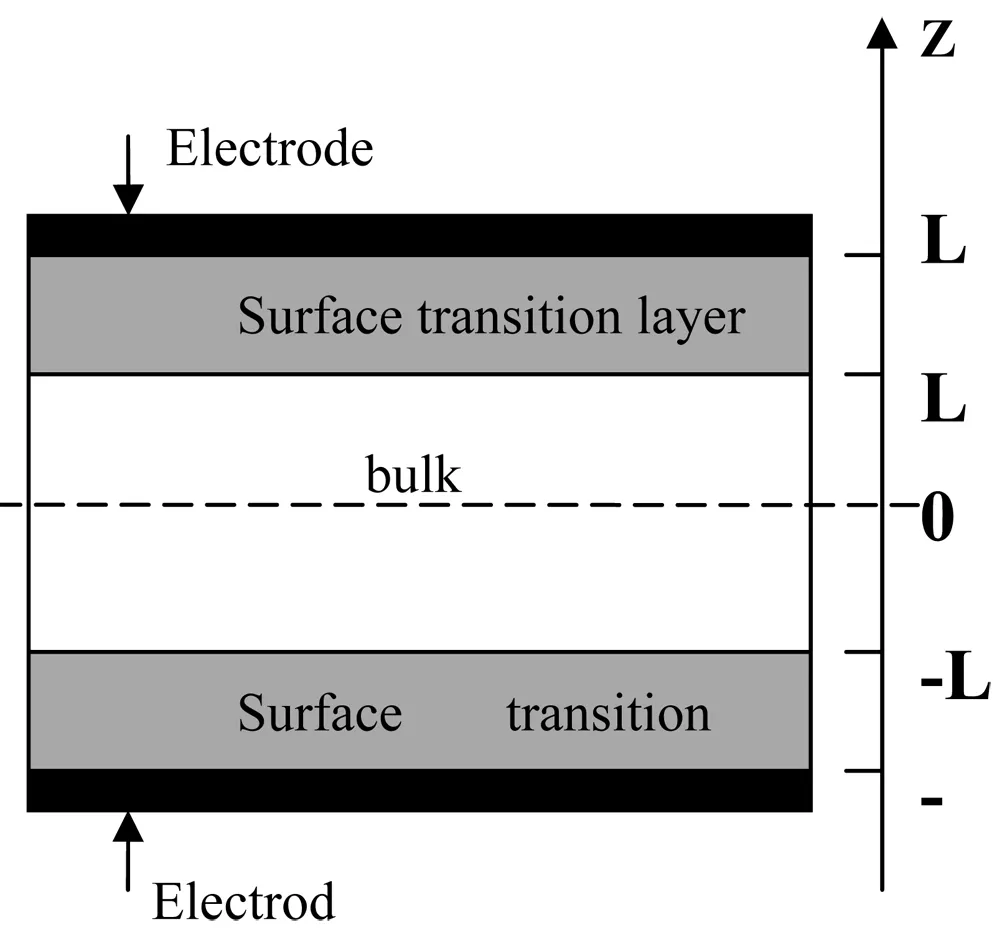
图1 含有表面过渡层的铁电薄膜结构

我们以二级相变铁电薄膜为研究对象进行数值计算。

平均相对介电常数为

(1)

其中

(2)

(3)

如果负责铁电相变的软膜位于布里渊区中心，那么薄膜的软膜频率为

(4)

由于

〈Q〉=P/nq

(5)

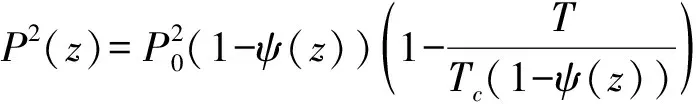
(6)

其中，n——单位体积的原胞数；q——振动离子的有效电荷量(绝对值)。

我们可以将方程(4)写为

(7)

其中，Tc——体材料的居里温度；P0——是零温时的饱和极化强度。

最后得到

(8)

(9)

(10)

其中，Γ(ζ)——重整化后的铁电薄膜的阻尼；Ω(ζ)——重整化后的铁电薄膜的软模频率。

(11)

(12)

为保证在任意位置处体系都处于稳定的铁电相，体系应满足条件Ω2(ζ)>0。

由于目前实验上还没有关于ψ(ζ)函数具体形式的报导，数值计算中常假设ψ(ζ)可以简单的表示成如下关系，这种假设并不影响结论的一般性[100]：

(13)

式中l2S，l1S——分别表示上下表面过渡层在薄膜中的边界位置；λ2，λ1——分别表示上下表面过渡层对体系饱和极化的影响程度。

假设η1,η2表示单个表面过渡层占薄膜厚度的百分比，即相对厚度，定义η1=(l-l1S)/2l和η2=(l-l2S)/2l。

在以下的计算中，取薄膜两个表面过渡层是对称的构型，所以，η=η1=η2,λ=λ1=λ2，并且令表面过渡层的厚度为lS=l-l1S=l-l2S。

2 数值结果和讨论

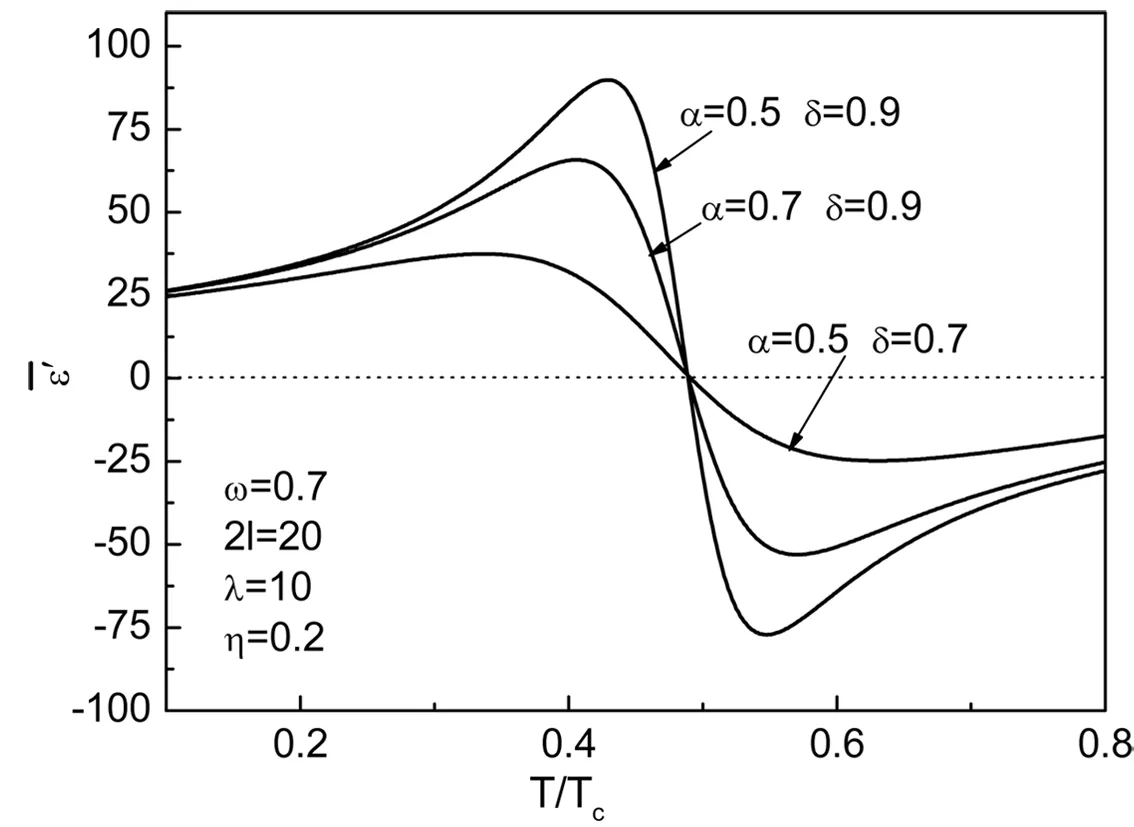
(a)

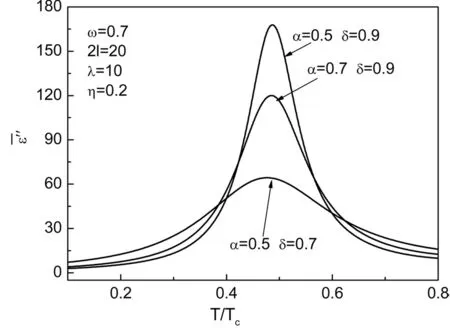
(b)

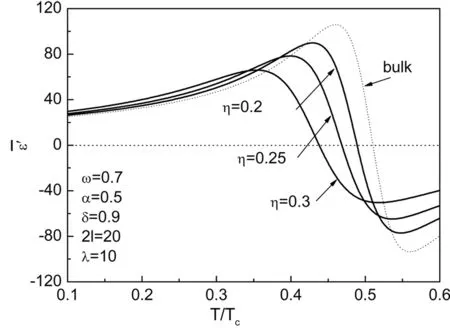
(a)

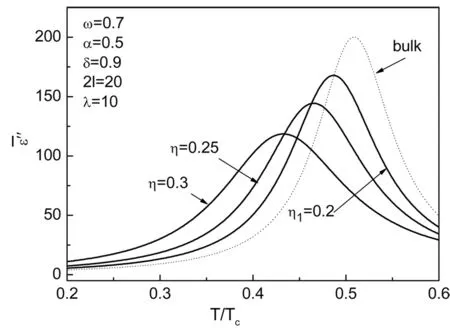
(b)

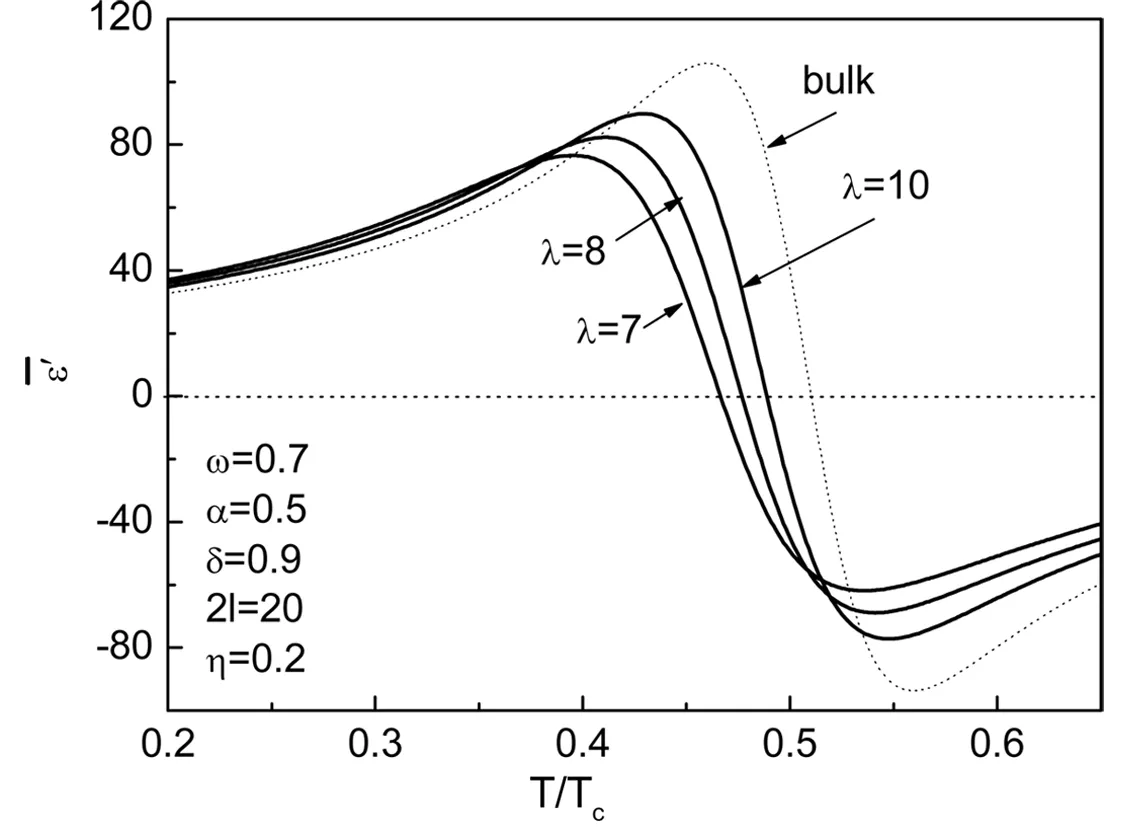
(a)

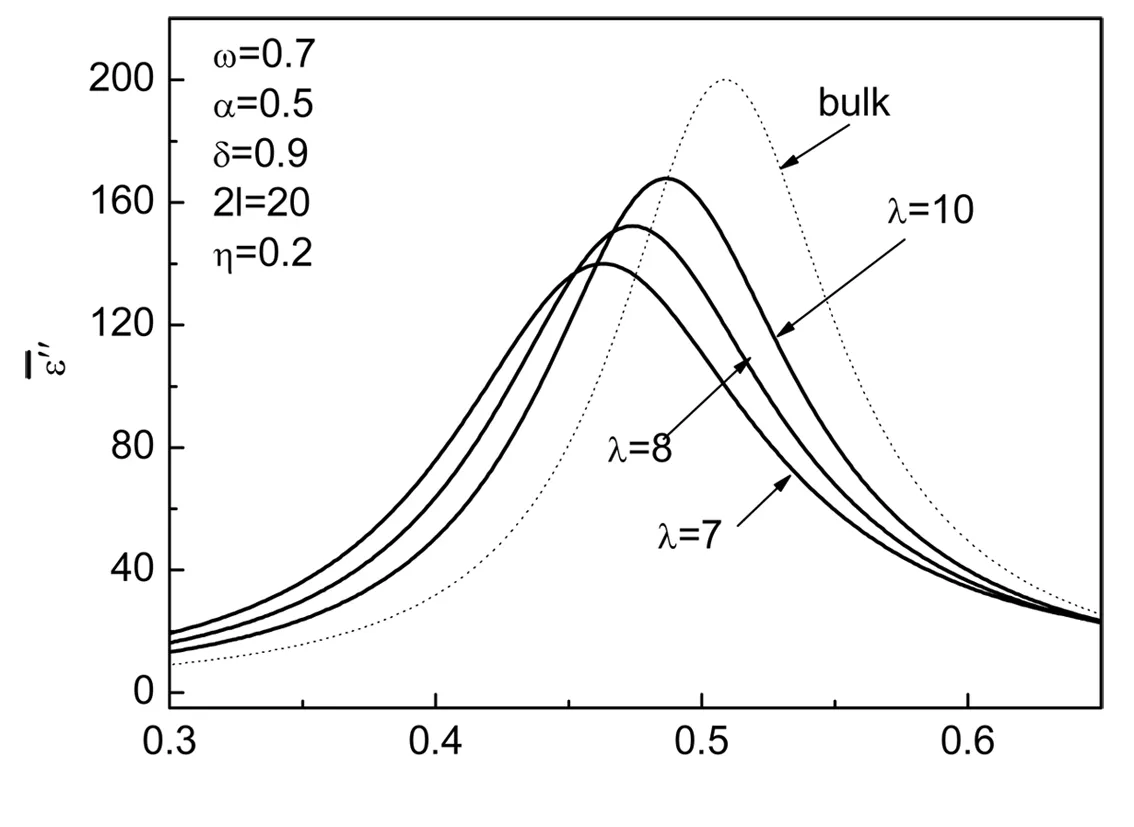
(b)

3 结语

本文在平均场近似的软膜理论基础上，研究了含有表面过渡层的铁电薄膜的介电函数随温度变化的动态性质，得到了定性的结论：表面过渡层对铁电薄膜的介电函数性质的影响不能忽略；随着表面过渡层作用的增加，铁电薄膜的介电函数的实部和虚部像低温移动，并且峰值降低。

[参考文献]

[1] M. Misra, K. Kotani, T. Kiwa,et al. THz time domain spectroscopy of pulsed laser deposited BaTiO3 thin films[J].Appl Sur Sci., 2004, 237: 421-426.

[2] S.K. Streiffer, C. Basceri, C. B. Parker,et al. Ferroelectricity in thin films: The dielectric response of fiber-textured (BaxSr1-x) Ti1+ yO3+zthin films grown by chemical vapor deposition[J]. J. Appl. Phys.,1999, 86: 4565- 4575.

[3] A.A. Sirenko, C. Bernhard, A. Golnik, et al. Soft-mode hardening in SrTiO3 thin films[J].Nature,2000, 404: 373-376.

[4] D.A. Tenne, A. Soukiassian, X.X. Xi,et al. Lattice dynamics in BaxSr1 xTiO3 thin films studied by Raman spectroscopy[J]. J. Appl. Phys., 2004, 96: 6597-6605.

[5] Ikufumi Katayama, Hiroshi Shimosato, Masaaki Ashida, et al. Thickness dependence of the soft ferroelectric mode in SrTiO3 thin films deposited on MgO[J]. J. Luminescence.,2008, 128: 998-1000.

[6] J.M. Wesselinowa. Dynamical Properties of Thin Ferroelectric Films Described by the Transverse Ising Model[J].Phys. Stat. Sol., 2002, 231: 187-191.

[7] T. Lü,W. Cao. Generalized continuum theory for ferroelectric thin films[J].Phys. Rev. B,2002, 66: 024102-1-024102-5.