烷基-取代自由基闭环反应的区位选择性

徐 珍 珍, 赵 东 霞, 杨 忠 志

( 辽宁师范大学 化学化工学院, 辽宁 大连 116029 )

0 引 言

取代的5-己烯自由基进攻双键碳原子而形成五元或六元环的分子内加成反应,在有机合成中引起了广泛的兴趣,被很多的实验[1-2]和理论化学家[3-5]所研究。图1所示即为烷基取代的5-己烯自由基的闭环反应。该反应有两种反应途径:一种是自由基C1进攻5号双键碳原子生成五元环产物,称为5-exo型；另一种是自由基进攻6号碳原子生成六元环产物,称为6-endo型。实验上一般认为,5-己烯自由基的环化加成(反应1、2、4、5)具有较高的区位选择性,形成的是五元环产物[1,4,6-8]。然而,当C5位置上有取代基(反应3),将会由于空间位阻效应,而生成6-endo型产物[5-7,9]。反应6和7也是由于空间效应,以生成大环为主要产物[3-4]。

1. R1=H, R2=H, R3=H, R4=H 2. R1=Me, R2=H, R3=H, R4=H 3. R1=H, R2=Me, R3=H, R4=H 4. R1=H, R2=H, R3=Me, R4=H 5. R1=H, R2=H, R3=Me, R4=Me 6. R1=Me, R2=H, R3=Me, R4=H 7. R1=Me, R2=H, R3=Me, R4=Me

图1 烷基-取代的自由基闭环反应分别生成5-exo型异构和6-endo型异构的产物

Fig.1 The alkyl-substituted radical ring closure additions, producing two isomers, 5-exoand 6-endoisomers

本文主要是利用Fukui函数和广义Fukui函数[10],分别结合局域HSAB原理,预测图1中所示的7个烷基-取代的自由基闭环反应的区位选择性以及反应之间的活性序列,其中活性指标是利用ABEEMσπ方法[11-14]获得的。

1 理 论

1.1 Fukui函数和广义Fukui函数

Fukui函数,f(r),是概念密度泛理论中预测分子活性位点的重要反应性指标之一,Parr和Yang等[15]将其定义为

(1)

根据HSAB原理以及局域HSAB原理,提出了广义Fukui函数[10]fG(r)的概念,如式(2)所示：

fG(r)=NMf(r)

(2)

其中,NM为体系的原子个数。从它的定义式中可以看出,广义Fukui函数是归一化到原子个数NM的,并且体系中任意r处的活性不仅与电荷的变化f(r)相关,而且还与体系的原子个数NM相关。

1.2 局域硬软酸碱(HSAB)原理

局域HSAB原理指出[16],两个分子发生反应并不在Fukui函数最大的地方,而是发生在局域软度(局域软度等于体系的整体软度与Fukui函数的乘积)几乎相等的地方。由于本文所研究的反应属于分子内的反应,因而整体软度为一定值,所以使用Fukui函数即可,即分子内的反应是发生在Fukui函数几乎相等的地方。使用中心原子的Fukui函数或广义Fukui函数差的绝对值(Δf或ΔfG)来体现这一原理,如式(3)和(4)所示：

Δf=|f1-f5/6|

(3)

(4)

2 计算细节

本文所有反应物均是在UB3LYP/6-311++G(d,p)方法下,使用Gaussian-03程序优化得到的。在同样的基组和方法下进行振动频率的计算,均无虚频出现。反应物中心原子的Fukui函数和广义Fukui函数是通过ABEEMσπ模型[11-14]得到的。

3 结果与讨论

3.1 反应物的构象

以5-己烯自由基的闭环加成反应(反应1)为例,在UB3LYP/6-311++G(d,p)水平下,通过改变二面角φC1C2C3C4和φC2C3C4C5的角度,从-180°～180°,每隔10°改变一次,获得了如图2所示的能量曲线。从图中可以看出,共获得了5个能量最低的构象,分别是转动二面角φC1C2C3C4,得到1-c(cc)、1-b和1-a；而转动二面角φC2C3C4C5得到了1-bb(b)、1-e(ee)和1-d三个构象,其中a、b(bb)和d型构象属于near-attack型构象,而c(cc)和e(ee)属于直线型构象。其中,直线型构象1-c(cc)和1-e(ee)的能量最低,而1-e(ee)型构象又是直线型中能量最低的。尽管1-b(1-bb)的能量低于1-a和1-d,但是从它们的结构上来看,1-a和1-d中自由基碳原子距离C5原子要更近一些,因此更容易发生自由基进攻反应。因此,选择构象1-a、1-d和1-e作为研究对象。其他反应物也能够得到与图2相类似的能量曲线,因此,在后面的讨论中选择构象a、d和e作为研究对象。

3.2 区位选择性的预测

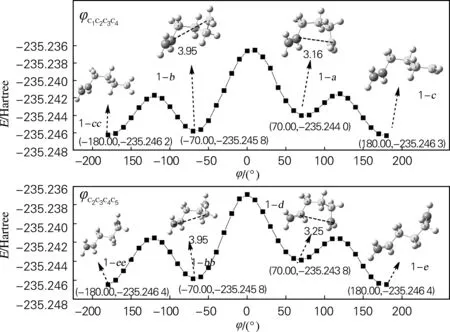
图2 UB3LYP/6-311++G(d,p)水平下,改变5-己烯自由基中的二面角φC1C2C3C4和φC2C3C4C5所得到的能量曲线(括号中所列的是二面角的角度和所对应的构象的能量)

Fig.2 The variation of the total energy with the dihedral anglesφC1C2C3C4andφC2C3C4C5of 5-hexenyl radical at the level of UB3LYP/6-311+ +G(d,p) (The angle and the energy of stable conformers are presented in the brackets)

3.3 反应间活性序列的预测

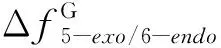
Δf5-exo×102Δf6-endo×102ΔfG5-exoΔfG6-endoExperimental rate constantsk5-exok6-endo1a1.110 62.072 60.188 80.352 3d1.095 22.016 60.186 20.342 8 1.000 00.020 0e1.197 52.292 30.203 60.389 72a0.300 82.940 00.060 20.588 0d 0.124 22.696 40.024 80.539 3e 0.077 43.063 00.015 50.612 63a6.781 72.317 91.356 30.463 6d6.704 32.349 31.340 90.469 9e6.853 52.708 41.370 70.541 74a0.681 32.114 50.136 30.422 9d0.569 52.167 40.113 90.433 5e0.515 62.470 10.103 10.494 05a0.410 12.738 90.094 30.630 0d0.406 42.602 00.093 50.598 51.400 00.020 0e0.085 22.766 20.019 60.636 26a4.905 92.956 71.128 40.680 0d4.777 73.242 31.098 90.745 70.022 00.040 0e5.218 73.220 51.200 30.740 77a4.201 72.823 51.092 40.734 1d4.296 22.788 21.117 00.724 9<0.000 20.020 0e4.473 13.193 41.163 00.830 3注:k是相对速率常数[4]。

4 结 论

在ABEEMσπ模型下获得的Fukui函数以及广义Fukui函数,结合局域HSAB原理,能够很好地预测烷基-取代的自由基环化反应的区位选择性。此外,主要产物的广义Fukui函数,还能够准确地预测出这一个系列反应之间的活性序列,与实验测得速率常数有很好的关联一致性。广义Fukui函数作为分子间的反应性指标,在预测分子内反应间的活性序列方面,也能够取得令人满意的结果。

[1] BECKWITH A L J, EASTON C J, SERELIS A K. Some guidelines for radical reactions[J]. Journal of the Chemical Society, Chemical Communication, 1980(11):482-483.

[2] MIRANDA N, DAUBLAIN P, HORNER J H, et al. Carboxylate-substituted radicals from phenylselenide derivatives. Designs on models for coenzyme B12-dependent enzyme-catalyzed rearrangements[J]. Journal of the American Chemical Society, 2003, 125:5260-5261.

[3] TUZUN N S, AVIYENTE V. A computational study on the substituent effect of diallylamine monomers in their cyclopolymerization reactions[J]. The Journal of Physical Chemistry A, 2002, 106:8184-8190.

[4] BECKWITH A L J. Regio-selectivity and stereo-selectivity in radical reactions[J]. Tetrahedron, 1981, 37:3073-3100.

[5] LEACH A G, WANG R X, WOHLHIETER G E, et al. Theoretical elucidation of kinetic and thermodynamic control of radical addition regioselectivity[J]. Journal of the American Chemical Society, 2003, 125:4271-4278.

[6] BECKWITH A L J, BLAIR I A, PHILLIPOU G. Substituent effects on the cyclization of hex-5-enyl radical[J]. Tetrahedron Letters, 1974, 15:2251-2254.

[7] BECKWITH A L J, BLAIR I A, PHILLIPOU G. Preferential cis cyclization of 6-hepten-2-yl and related radicals. Example of orbital symmetry control[J]. Journal of the American Chemical Society, 1974, 96:1613-1614.

[8] WALLING C, CIOFFARI A. Cyclization of 5-Hexenyl Radicals[J]. Journal of the American Chemical Society, 1972, 94:6059-6064.

[9] BECKWITH A L J, LAWRENCE T. The effect of non-bonded interactions on the regioselectivity of cyclization of the hex-5-enyl radical[J]. Journal of the Chemical Society, Perkin Transactions 2, 1979(11):1535-1539.

[10] ZHAO D X, XU Z Z, YANG Z Z. Local HSAB rationalization of Diels-Alder reactions by means of ab initio and ABEEMσπ methods:stereoselectivity and reaction rate[J]. International Journal of Quantum Chemistry, 2012, DOI:10.1002/qua.24173 (in press).

[11] YANG Z Z, WANG C S. Atom-bond electronegativity equalization method.1. calculation of the charge distribution in large molecules[J]. The Journal of Physical Chemistry A, 1997, 101:6315-6321.

[12] WANG C S, YANG Z Z. Atom-bond electronegativity equalization method. II. Lone-pair electron model[J]. Journal of Chemical Physics, 1999, 110:6189.

[13] CONG Y, YANG Z Z. General atom-bond electronegativity equalization method and its application in prediction of charge distributions in polypeptide[J]. Chemical Physics Letters, 2000, 316:324-329.

[14] ZHAO D X, LIU C, WANG F F, et al. Development of a polarizable force field using multiple fluctuating charges per atom[J]. Journal of Chemical Theory and Computation, 2010, 6:795-804.

[15] PARR R G, YANG W T. Density-functional Theory of Atoms and Molecules[M]. Oxford:Oxford University Press, 1989.

[16] GAZQUEZ J L, MENDEZ F. The hard and soft acids and bases principle:an atoms in molecules viewpoint[J]. The Journal of Physical Chemistry, 1994, 98:4591-4593.