基于AHP复合熵的公路建设项目TOPSIS排序模型＊

2012-09-25李晓伟

武汉理工大学学报（交通科学与工程版） 2012年5期

李晓伟陈红马娟

（西安建筑科技大学土木学院1）西安 710055）

（公路大型结构安全教育部工程中心2）西安 710064）（长安大学公路学院2）西安 710064）

公路建设项目排序是公路网规划的重要内容，排序结果好坏直接影响着公路网规划的实施效果.目前，国内外学者对此进行了大量的研究［1－6］，构建了公路建设项目排序指标体系，提出了层次分析法、灰关联投影法、单元重要度分析、熵值法、动态改进以及模糊数学等公路建设项目排序方法，极大地推动了公路建设项目的科学化决策.本文在给出公路建设项目排序评价指标体系的基础上，提出了基于AHP复合熵的公路建设项目TOPSIS排序模型.该模型充分考虑了专家知识经验以及数据本身蕴涵的信息，采用AHP与熵值法综合确定了评价指标的权重，以求同时反映专家知识经验的主观性和实测数据的客观性.同时，通过构建加权标准化决策矩阵，计算公路建设项目与正负理想方案的距离，进而计算公路建设项目与正理想方案的贴近度来确定公路建设项目的实施序列.最后，将该模型应用于5条公路建设项目排序，验证了该模型的实用性与有效性.

1 公路建设项目排序影响参数

本文在借鉴前人研究成果［7－10］的基础上，从公路建设的紧迫性、公路在公路网中所处地位的重要性、公路建设的经济性以及交通改善效果等角度出发，选择路段饱和度等6个具有代表性的分项指标组成排序影响参数体系，如表1所列.

表1中，路段饱和度和路段行政级别系数主要从交通负荷强度和交通矛盾突出程度反映公路建设的紧迫性；路段重要度系数主要反映路线在促进区域经济发展上的重要程度；内部收益率主要从公路建设带来的效益角度考虑项目建设的要求；交通服务质量改善率及交通运行效率改善率则主要从提高路网运行效率和交通质量的角度考虑项目的建设需求.

表1 公路建设项目排序影响参数

2 公路建设项目TOPSIS排序模型

公路建设项目排序，设有n个待选的排序项目A＝｛A1，A2，…，An｝，影响参数为C＝｛C1，C2，…，Cm｝，N＝｛1，2，…，n｝，M＝｛1，2，…，m｝，i∈N，j∈M，参数的权重为 w＝（w1，w2，…，wm），Y＝（yij）n×m表示项目集Ai对参数集Cj的决策矩阵：

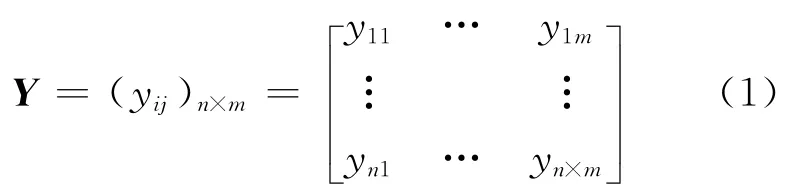
2.1 标准化决策矩阵

对参数进行标准化处理，基于影响参数的计算方法和含义分析，可知影响参数Cj均为效益型指标.

则指标决策矩阵标准化处理后可表示为

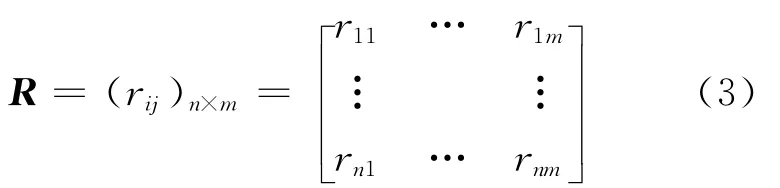
2.2 确定影响参数权重

权系数是以某种数量形式对比、权衡被评价事务总体中诸因素相对重要程度的量值，针对同一组指标数值，不同的权重系数会导致截然不同的评价结论.考虑到公路建设项目排序过程中既包含专家群体的知识、经验和价值的判断等主观因素，也有实际调查数据的客观信息特征，因此本文将主观赋权法（层次分析法——AHP［11］）和客观赋权法（熵值法［12－13］）结合起来确定评价指标的权重，以求更客观全面地反映评价指标的重要性和问题的实际情况.设AHP法给出的主观权重为w′i，熵值法给出的客观权重为 w″i，则最终确定的权重wi为

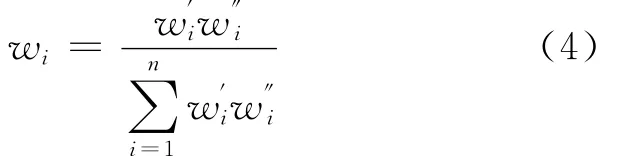
2.3 构造加权标准化决策矩阵

将标准化决策矩阵和评价指标权重相结合构造加权标准化决策矩阵Z＝（Zij）m×n.式中：zij＝rijwj.则加权标准化矩阵可表示为

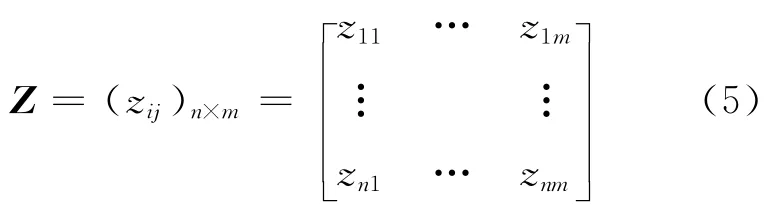
2.4 确定正负理想项目方案

由于评价指标均为效益型指标，因此借鉴TOPSIS思想可确定加权标准化决策矩阵的正负理想项目方案为

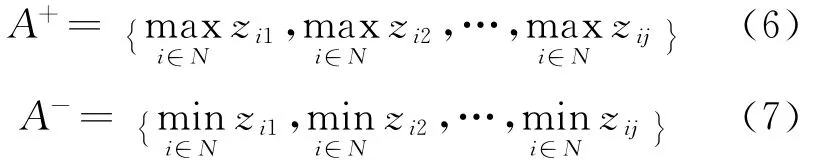
2.5 计算距离与相对贴近度

设公路建设项目Ai到正理想方案的距离为，到负理想方案的距离为.则

则0＜fi＜1，当fi接近0时，愈接近0，公路建设项目Ai愈靠近负理想方案，该项目建设需求就愈低；当fi接近1时，愈接近0，方案愈靠近正理想方案，则该项目的建设需求就愈高.

3 实证研究

以某市规划建设的5条公路为例，应用本文的方法对其进行排序，以验证模型的有效性与实用性.通过调查，5条公路建设排序参数属性值计算结果如表2所列.

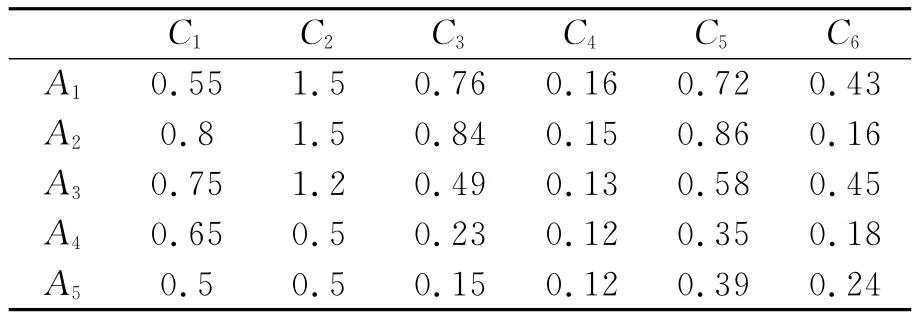
表2 各方案的决策指标计算值

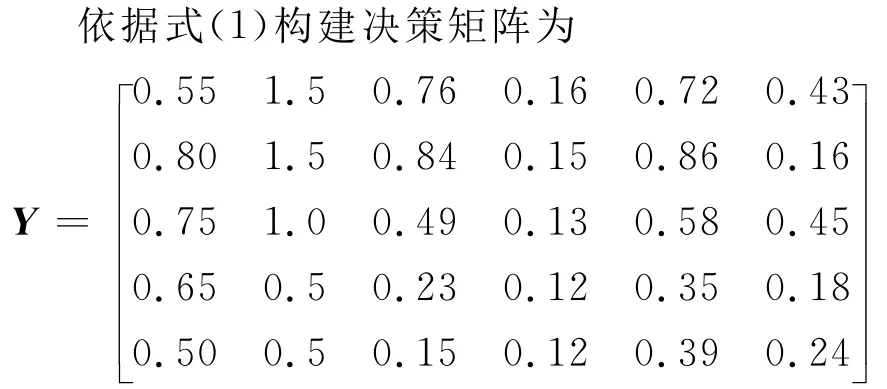
3.1 标准化决策矩阵

依据式（3）将决策矩阵标准化为

3.2 确定影响参数权重

1）AHP确定权重应用1～9标度法构建目标层矩阵和指标层矩阵，在对各判断矩阵进行一致性检验的基础上，通过对矩阵进行层次单排序和层次总排序，可计算指标参数权重如表3所列.

表3 应用AHP确定的参数权重

2）熵值法确定权重因为影响参数指标有6个，即m＝6.

表4 熵值法确定的参数权重

3）综合权重根据AHP法和熵值法确定的权重，应用式（4）确定各指标参数的综合权重wi，计算结果如表5所列.

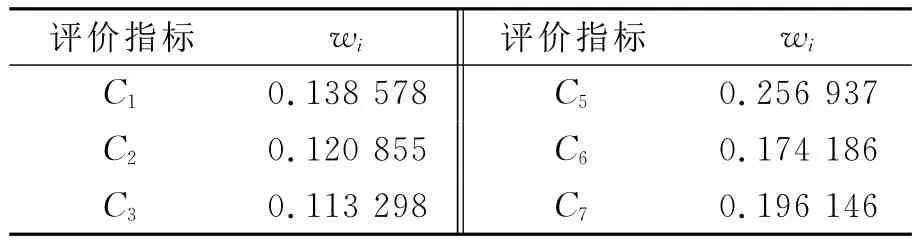
表5 参数的综合权重

3.3 构造加权标准化矩阵

应用式（5）构造加权标准化矩阵为

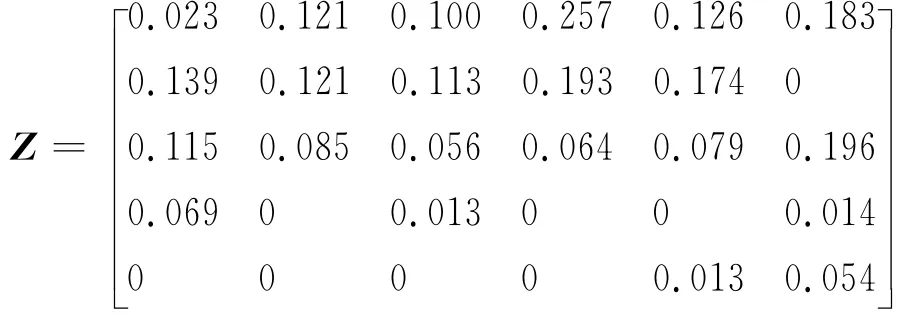
3.4 确定正负理想方案

应用式（7）确定正负理想方案为

3.5 计算距离及相对贴近度

应用式（8～9）计算建设项目Ai到正负理想方案的距离：＝0.126，＝0.375；＝0.206，＝0.338；＝0.227，－＝0.269；＝0.399，＝0.072；＝0.398，＝0.056.

应用式（10）计算建设项目Ai到正理想方案的贴近度：f1＝0.748，f2＝0.621，f3＝0.543，f4＝0.153，f5＝0.123.

故知：f1＞f2＞f3＞f4＞f5.

4 结论

1）本文提出了一种基于AHP复合熵的公路建设项目TOPSIS模型，该模型在构建公路建设项目决策实施矩阵并将其标准化的基础上，结合评价指标权重建立加权标准化决策矩阵，引入运筹学的TOPSIS法确定了决策矩阵的正负理想方案，通过计算公路建设项目与正负理想方案的距离及贴近度来确定公路建设项目的实施序列，为公路建设项目排序提供了一种新途径.

2）本文将主观赋权法——AHP和客观赋权法——熵值法结合起来确定评价指标的权重，充分考虑了专家知识经验以及数据本身蕴涵的信息，能够更客观全面地反映评价指标的重要性和公路建设项目的实际情况.

3）以5条公路建设项目排序为例，应用本文提出的模型对其进行实证分析，验证了该模型的有效性与实用性；研究成果对于统筹安排公路建设时序、科学合理利用资金、减少盲目投资所造成的经济损失等具有重要的理论价值与现实指导意义.

［1］曲大义，王炜，邓卫，等.层次分析法在公路网规划建设项目排序中的应用［J］.公路交通科技，2000，17（5）：102－106.

［2］崔洪军，陆建，王炜.基于多目标灰关联投影法的道路建设项目排序模型［J］.交通运输工程与信息学报，2004，2（3）：83－87.

［3］梁颖，陈艳艳，任福田.基于单元重要度分析的公路网规划项目建设序列论证［J］.北京工业大学学报，2005，31（3）：284－287.

［4］罗君君.基于熵权的公路建设项目排序多目标决策分析［J］.华中科技大学学报：城市科学版，2006，23（3）：62－64.

［5］曹守华，袁振洲，沙滨，等.基于动态理论的公路建设项目序列安排［J］.交通与计算机，2005，23（4）：39－43.

［6］王秉纲，周伟.公路建设项目的模糊排序和投资决策优化［J］.中国管理科学，1997，5（2）：28－31.

［7］田硕.多目标决策下的公路建设项目优化排序研究［D］.西安：长安大学，2007.

［8］彭力.公路网规划评价指标体系与实施决策方法研究［D］.南京：东南大学，2005.

［9］李翠玲.公路建设项目实施序列优化研究［D］.长春：吉林大学，2006.

［10］朱辉.区域干线公路网规划布局方案评价方法研究［D］.长春：吉林大学，2006.