延误航班机场场面滑行优化调度策略研究＊

柳 青 李春玲 宋祥波

（南京航空航天大学民航学院1） 南京 210016） （中国民航大学经管学院2） 天津 300300）

枢纽机场场面控制问题（ASMCP）的核心是航空器路径规划及停机位分配.目前国外研究关注较多的是自动场面控制系统［1－2］、启发式算法求解航班调度次序［3］、场面运行控制和地面等待着陆［4］，以及对多跑道系统（阿姆斯特丹机场）的复杂调度以及高密度航班（达拉斯沃斯堡机场）的实证分析.国内现阶段研究主要使用多Agent仿真建模、TDSP动态算法等解决航空器路径规划和优化问题［5］.本文将延误航班按路径属性归类，依照流水车间作业调度方式对其进行滑行调度，是机场控制区调度作业的最新探索，能丰富处理延误航班应急调度的策略，有较为重要的实际意义.

1 延误航班滑行调度建模

1.1 问题分析

延误航班应急调度是指在出现天气、管制等原因后，高峰小时内大量的进港航班不能按计划到达时间（ETA）降落机场，滑入目标停机位.在出现航班不正常运行的紧急情况时，制定应急调度预案，重新分配调度方案，安排更高效的调度计划是解决地面拥堵的重要途径.调度航班滑行必须遵守相关的安全标准，否则，遇到时刻变化和各种特殊紧急情况，航空器滑行容易产生三类场面冲突［6］，如图1所示.

图1 航班调度过程及滑行三类冲突

航班调度除推入推出目标停机位可能不同外，有大量航班具有同样的滑行路径.正常情况下，不同航空公司飞往不同目的地的不同航班交错进离港.一旦出现航班延误，既有航班计划将被打乱，机场在效率和安全压力下，可以考虑选择更简单、更快速的应急调度策略，流水作业法完全可以模拟车间流水线调度，将具有相同滑行路径的航班进行聚类，统一安排调度，解决大面积延误航班调度同时，有效规避滑行冲突，见图2.

1.2 假设条件

延误航班调度发生于特殊情况，模型建立需要满足一定的假设前提：（1）在时间（0，T）内有一组待降落的航班｛f1，f2，…，fi｝⊆Aarr和一组等待 起飞的航班｛f1，f2，…，fj｝⊆Adep由于特殊原因发生延误；（2）受所带油量限制，进港航班在空中等待落地的时间有限.同样，离港航班在关舱门后，发动机处于运转状态，不会无限期等待，离港等待滑行的时间有限；（3）在一个固定时段内，滑行边上任意节点一次只能通过一架航空器；（4）在一个固定时段内，一架航空器只能在一条滑行边上滑行.

图2 航空器滑行调度转化为流水车间调度过程

1.3 相关符号及模型建立

将经典车间流水线作业的思想应用于应急航班调度建模，具体过程可描述为：在应急高峰时段内有n个需要调度航班fi（i＝1，2，…，n）在m 条滑行道边Rj（j＝1，2，…，m）上滑行，这n个航班依据路径属性可以归类成l组航班簇.在一个航班簇内，航班fi的滑行路径Ri，j（j＝1，2，…，ml），航班滑行路径Ri，j必须通过滑行边Rj，滑行时间记为pi，j.调度目标是在满足路径的要求下，为每架航空器寻找到一条有时间限制的路线，最终使所有航空器总调度滑行时间最小，由此建立延误航班流水调度模型：

模型中，决策变量ti，k为航班i在滑行道Rk上完成滑行的时间；pi，k为航空器i在Rk边上的滑行时间；xijk为二进制决策变量，表示指示变量.如果航班fi在航班fj之前在Rk上滑行，则xijk＝1，否则，xijk＝0；aihk为二进制决策变量，表示指示系数，若航空器i在滑行边h上滑行的次序先于滑行边k，那么aihk＝1，否则记为0；M 为一充分大的正整数；Tsep为不同机型之间按照规定要求的滑行间隔时间，根据不同重量机型选取不同的间隔距离值，用公式Tsep＝dsep／¯v来计算两架飞机最小时间间隔，¯v取值飞机的平均速度.ATAi为到达航班fi的实际降落时间；OBTi为起飞航班撤轮档时间，TTDi为离港航空器的结束滑行的起飞时间.

目标函数（7）指调度优化的总目标是所有进离港航空器调度滑行时间最少；约束（8）为航空器通过滑行边的次序，除了满足滑行时间外，还需要符合民航局规定的最小安全间隔；约束（9）为航空器在不同滑行边上的滑行顺序；约束（10）为降落航班的实际到达时间，也即起始滑行时间；约束（11）为离港航班的实际起飞时间；约束（12）为每架航空器必须降落到地面或者撤开轮档才能开始滑行；约束（13）为对滑行完成时间的正数约束.航班预计降落时间ATAi和撤轮档时间OBTi由空管调度给出时间表；约束（14）为对二进制变量的描述.

2 多粒子群求解算法设计

2.1 粒子群算法求解滑行调度

粒子群算法（particle swarm optimization，PSO）是Kennedy和Eberhart在1995年提出的群智能优化算法，针对NP复杂问题求解，粒子群算法有时间和效率的优势［7－8］，粒子群算法求解调度问题的主要步骤包括：

1）编码机制 首先对模型的参数进行编码.由于调度是基于操作为基础，粒子的顺序代表了调度顺序.用d＝n×m表示微粒的位置矢量，一个粒子可以表示为d维向量，每架航空器均会出现m次.将微粒转化为有序的操作表，再根据每架航空器滑行时间进行调度，进而产生调度方案.举一个3架进场航空器在5条滑行边上滑行的例子，粒子位置 X＝［1，2，3，4，5，2，3，1，5，4，4，1，5，3，2］，根据航空器滑行次序（见表1），路径R1的通过顺序是J1－J2－J3，路径2的调度次序是J2－J1－J3.

表1 航空器滑行次序

2）适应度函数 适应度函数用来评价粒子的性能，函数目标是最小化调度时间，考虑到航空器的安全间隔因素，也就是约束条件（8）.因此，算法用目标函数

M（1－xijk）×min｛tj，k－ti，k－pj，k－Tsep，0｝作为候选方案的适应度函数，其中M（1－xjk）×min｛tj，k－ti，k－pj，k－Tsep，0｝作为约束条件放入到目标函数的惩罚项，一旦最小安全时间间隔小于规定值，则粒子的适应度函数加上无限大的正数项，可以避免进入下一次迭代.

2.2 多粒子群（CPSO）粒子群算法

多粒子群算法步骤如下.

步骤1 根据初始调度计划，计算各航空器在各自路径集Ri上的理想滑行时间.

步骤2 根据延误航班的滑行路径属性进行聚类，同时考虑起降时刻间隔满足等待时间约束的一类航班划分为一组航班簇.

步骤3 设置2层粒子参数，全局最优粒子种群和5个子种群，计算初始子目标值.

步骤4 从5个最优子种群中找出最优适应度函数值Ztemp与当前全局最优适应度最优值进行比较，如果优于，则用新的适应度函数值代替前一轮的最优值.用相应新粒子代替原来的粒子，得到此状态下的每个粒子的个体最优解Xpi.

步骤5 在最优种群的基础上重新产生5个子种群，利用式（8）、（9）移动粒子，产生新的粒子群，重复步骤5，直至完成设定的迭代次数.

步骤6 将Ztemp与目前的适应度最优值进行比较，如果优于，则用新的适应度函数值代替前一轮的最优值.用相应新粒子代替原来的粒子，得到此状态下的每个粒子的个体最优解Xpi.

步骤7 计算调度时间，得到调度方案.

3 算例分析

依算法步骤，首先根据延误航班进离港调度路径和停机位进行属性聚类，延误航班滑行路径可以分为6组待调度的航班簇，见表2.每组航班簇有相同或者相近的停机位，再对6组航班簇进行滑行调度优化.

表2 聚类航班簇流水车间调度

图3 延误航班流水调度

求解航班应急调度模型，设置种群数50，最大迭代次数100，惯性因子0.4.同时，根据每组航班簇的航空器数量不同，设置多粒子种群个数，分别为4，4，2，1，3，4组粒子分别计算.依照假设条件中的风险级别规定，待降航班的调度优先级大于起飞航班，调度过程如图3所示.

从图4的计算结果看，多粒子群算法不到80代即收敛得到全局最优解.但是，多粒子群算法在计算局部小规模的航班簇调度中，相比FCFS方式总体优势不明显，每个局部最优的总和2 501s的总体调度时间效率仅仅提高98s；当将所有延误航班看成一个整体进行全局流水航班调度时，总体调度时间为1 745s，较之FCFS提高了854s（14.2min），见表3.调度结果，对编排新的调度计划有非常有意义的参考价值.

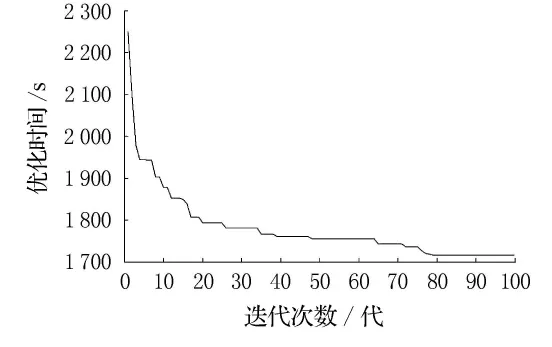
图4 迭代次数与最优解

表3 航班调度结果比较 s

5 结 论

1）延误航班调度问题可以转化为车间调度中特殊的流水线调度方法，处理延误航班需要分析和正确归类有类似属性的航班计划，模拟流水车间处理具有相同工序工件的方式.

2）建立的延误航班应急调度模型可以用来求解不正常航班调度计划，以此提高机场场面控制部门的调度效率和机场容量.通过适应性改进后可以应用于枢纽机场单跑道场面的延误航班调度，具有一定的实际参考价值.

3）多粒子群算法在处理大规模复杂优化问题方面具有时间效率和解空间快速收敛的优势，可以作为此类模型可靠的求解算法之一.

［1］赵文智，王化佳.一个航班备降延误的成本分析［J］.中国民航大学学报，2009，12（6）：45－47.

［2］CAPOZZI B J，DIFELICI J.Towards automated airport surface traffic control：potential benefits and feasibility［C］／／ AIAA Guidance，Navigation，and Control Conference and Exhibit，2004（8）：1－16.

［3］RATHINAM S，MONTOYA J，JUNG Yoon.An optimization model for reducing aircraft taxi times at the dallas fort worth international airport［C］／／26th International Congress of The Aeronautical Sciences，2008：1－14.

［4］ANAGNOSTAKIS I，CLARKE J P.Runway operations planning：a two－stage solution methodology［C］／／Proc.of the 36th Hawaii International Conference on System Sciences（HICSS′03），2003：1－12.

［5］尤 杰，韩松臣.基于多智能体MAS的智能交通控制系统的研究［J］.交通运输工程学报，2009，2（1）：109－113.

［6］王艳军，胡明华，苏 炜.基于冲突回避的动态滑行路径算法［J］.西南交通大学学报，2009，12（6）：933－940.

［7］王万良，周 明，徐新黎，等.基于改进粒子群算法的离子膜车间调度问题研究［J］.控制与决策，2010，25（7）：1021－1025.

［8］李爱国.多粒子群协同优化算法［J］.复旦学报：自然科学版，2004，43（5）：923－925.