公交发车频率与交叉口信控参数的协调关系研究＊

柏海舰 董瑞娟 李文权 张卫华

（合肥工业大学交通运输工程学院1） 合肥 230009） （东南大学交通学院2） 南京 210096）

0 引 言

公交优先的理念已被大多数城市广为接受，优先不仅仅需要宏观政策上的引导，也需要微观技术上的支撑.公交车辆在道路上的优先主要体现在路权优先和信号优先2种形式，本文研究了上游交叉口信号控制参数与公交站点停靠线路发车频率的协调关系，充分体现了公交在微观上的优先.国内外关于交叉口内公交信号优先［1－3］的研究内容较多，但交叉口信控参数与下游公交站点的关系研究极少.有些学者研究了信控条件下的交通间断流模型，但对间断流条件下公交车流特性研究很少.公交站点由于公交车流的短时集中而拥堵的现象屡见不鲜，红灯闲，绿灯堵，严重降低公交站点的服务水平，影响相邻车道的车辆正常运行.因此，研究站点线路发车频率与上游交叉口信控参数的协调关系及其优化方法对缓解公交站点处的拥堵有着重要的作用.本文从间断公交车流形成机理及其特征参数的研究出发，建立间断公交车流特征参数与交叉口信控参数的关系；分析下游公交站点的运行特征，推导间断公交车流条件下，下游公交站点通行能力需满足的公式，从而构建公交站点停靠线路发车频率与上游交叉口信控参数之间的协调关系式.通过实例计算，对二者的关系模型进行求解，验证模型及求解方法的合理性.

1 间断公交车流的特性分析

如图1所示，交叉口的车流运行示意图中，交叉口为4相位信号控制，可假设西进口直行车道的通行能力为Qs，进口直行车道的车流量为qs，交叉口西进口的绿灯时间为tg，信号周期为T.由西进口直行并停靠下游站点的公交车流的总到达率为λs＝ ∑λi.式中：λi＝60／Ni，Ni为第i条线路的发车频率，辆／min.

由图1可见，交叉口下游的交通流由于受信号影响，形成间断交通流.同理，公交车流作为交通流的一部分也形成间断流.因此可根据车流波动理论计算间断公交车流中公交车辆的平均到达率.假设直行绿灯时间内直行车道通过车辆数与通行能力相同，则在直行绿灯时间内，通过的公交车辆数m为

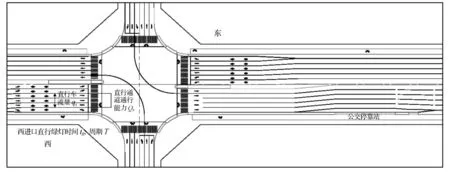
图1 公交站点与上游交叉口关系示意图

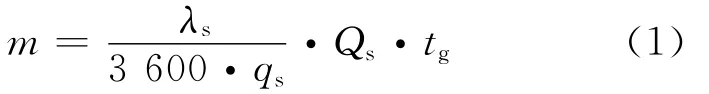
设间断公交车流中连续段的公交车辆到达率为λ，则λ和m满足

将式（1）代入式（2）得

通常左转车流流量相对较小，且其中的公交车流量也较少，本文暂不考虑南北相位公交车流所形成的短间断流，只以直行间断流作为研究对象.红灯闲，绿灯堵的现象主要是因为短时间内有多辆公交车辆到达站点，超过站点的泊位数而导致排队拥堵.因此分析一段车流中，公交车辆的到达特性显得尤为重要.从整条道路来看，交通流呈现间断流特征；从间断流本身内部特性来看，其每一段又可以看作有限总体的简单流，且符合泊松分布规律.

2 间断流条件下站点－上游交叉口系统分析

2.1 站点系统运行特性

如图2所示，假设停靠站点有4个泊位，公交车辆减速进站时间为tj，站内平均上下客服务时间为td，公交车辆最小安全反应车头时距为ta，则1号车开始进站到5号车开始进站的时间间隔为tj＋td·（g／c）＋k·ta.g，T 分别为站点下游交叉口的绿灯时间和周期；B为站点的物理设施最大通过能力［4－7］.则有

图2 公交车进出站点运行示意图

2.2 站点－上游交叉口生灭系统特性

从前文分析可以看出，由于交叉口信控的影响，到达公交站点的公交车流呈现间断流，且每段车流符合泊松分布，符合生灭系统特征，且是有限输入总体的生灭系统，因此可采用生灭过程进行分析.如图3所示，其中λ表示间断流公交车辆中连续段的公交车辆到达率，即生灭系统的输入率；μi为站点的输出率；si为系统中有i辆公交车的状态.

图3 有限输入总体的生灭系统示意图

根据生灭系统［8－9］的数学公式得出路内站点生灭状态方程组.

对于站点系统中没有车辆的状态即i＝0时，其状态方程为

对于站点系统中有i辆公交车的状态其状态方程为

式中：Pi为站点同时有i辆车到达的概率，i＝0，1，2，….

根据式（6）、式（7）递推可得

根据式（8）～（10）可通过数学归纳法推导证明k个泊位的站台其P0的计算式为

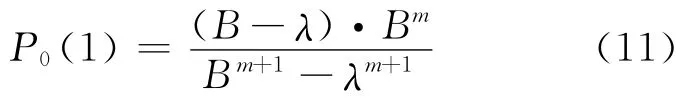
式中：P0（k）为k个泊位数的站点有0辆车到达的概率，即有k个泊位数站点的P0值.

根据停靠站泊位数不同，联立公式（8）、（9）、（11）、（12）可解得不同泊位数的站点计数间隔时间内公交车辆到达的概率为

2.3 公交站点停靠线路发车频率与上游信号控制的关系［10－13］

根据左转车流量大小，交叉口的信号控制形式可分为设左转专用相位和不设左转专用相位.设左转专用相位的信控交叉口其左转车流量较大，左转车流形成的间断流也需要考虑.但从信号相位图可以看到，可以通过直－左－左－直或左－直－直－左的相序排列将左转间断流与直行间断流分开.一般情况下直行间断流比左转间断流长，对下游的影响更大，应作为主要研究对象.而对于不设左转相位的交叉口，其左转车流量小，在不影响分析合理性的情况下可不作考虑.因此，采用4相位的信控形式下直行间断流为例建立二者的关系方程.

考虑到实际车流运行的随机性，即使正常车流，也可能出现站点偶尔排队，研究的重点应该是避免经常性排队而不是偶发性排队.因此采用车辆进站排队的概率作为间接指标来评价站点的拥堵状况，间断流排队概率的计算应分为2个部分：（1）间断流中分段车流含有k辆或k辆以上公交车的概率β；（2）含有k辆或k辆以上公交车的分段车流在站点出现排队的概率α，限于篇幅论文未讨论α，β的取值，可根据不同城市的实际情况取定，这里暂取为0.3，据此可得如下方程

联立式（2），（3），（16），（17）构成了λ，λs，m，Qs，tg，T的关系方程组，即公交站点停靠线路发车频率与上游交叉口信控参数的协调关系方程组.通常情况下，交通口的信号周期可通过相关交叉口交通量及区域控制策略分析计算得出，T可看成已知量.

公交站点停靠线路发车频率与上游交叉口信控参数的协调关系可体现在以下2个方面：（1）下游公交站点发车频率已定，如何确定上游交叉口信控参数；（2）上游交叉口信控参数已定，如何调整下游公交站点停靠线路的发车频率.从关系方程组可以看到，已知信号周期T和λs，解方程组得上游交叉口的直行绿灯时间；已知信控参数T，tg，可解得下游公交站点停靠线路的发车频率λs.因此该关系方程组从理论上确定了公交站点停靠线路发车频率与上游交叉口信控参数的协调关系.

3 实例分析

选取南京市北京东路－丹凤街交叉口及北极会堂公交停靠站作为实例分析对象，调查、整理得如下基本数据：上游路口信号控制周期为150s，东西直行绿灯时间65s，东西左转绿灯时间19s，东西红灯时间60s；交叉口进口两直行车道车辆到达率为1 025pcu／h.北极会堂公交停靠站距离下游交叉口25m，受下游交叉口信号灯影响、站台停靠13条线路、下游交叉口g／c＝80／154＝0.519，td＝32s，站台车位数为4，站点公交车辆的到达率为138bus／h.

采用式（4～5）可计算得站点物理设施的通过能力为 B＝222bus／h，μ1＝76bus／h，μ2＝135 bus／h，μ3＝183bus／h.取α＝0.3根据调查得T＝150s，λs＝138bus／h，可由关系方程组解得与下游站点停靠线路发车频率相协调的直行车流绿灯时间t′g＝53＜65s；同理，由tg＝65s，解得在间断流条件下，满足站点通行能力的停靠线路发车频率的值λ′s＝107bus／h＜138bus／h.该站点高峰时段，公交车辆排队进站车辆较多，与计算结果相吻合.可通过缩短上游交叉口东西向的直行绿灯时间和减少停靠站点线路的方法来改善当前站点车辆排队进站较多的情况，也进一步验证了论文推倒关系方程的正确性.

4 结束语

影响公交线路运行效率的关键位置之一是公交停靠站，因此合理有效的解决公交车在公交站点的效率问题将能很大程度提高公交运行的效率，提高公交出行方式的优势.论文本着公交优先的理念，研究站点通行能力约束下，上游交叉口信控参数与下游公交站点的协调关系.对站点规划和交叉口信控参数的设定有参考作用，同时也是公交优先理念在微观技术上体现.

［1］HAMDOUCH Y，LAWPHONGPANICH S.Schedule－based transit assignment model with travel strategies and capacity constraints［J］.Transportation Research Part B：Methodological，2008，42（7／8）：663－684.

［2］ZHAO Xiaomei，GAO Ziyou，LI Keping.The capacity of two neighbour intersections considering the influence of the bus stop［J］.Physica A：Statistical Mechanics and its Applications，2008，387（18）：4649－4656.

［3］戴 帅，朱 晨，陈艳艳.城市公交系统的时间可靠度研究［J］.武汉理工大学学报：交通科学与工程版，2008，32（5）：869－871.

［4］Federal Transit Administration.Transit capacity and quality service manual 2nd edition［R］.Washington D C：Transit Cooperative Research Program （TCRP）Report 100，2003.

［5］柏海舰，李文权.常规公交站台容纳线路能力计算模型［J］.东南大学学报：自然科学版，2007，37（6）：1077－1080.

［6］柏海舰，李文权，孙 山.基于车流特性的路内公交站点通行能力［J］.系统工程理论与实践，2009，29（10）：174－179.

［7］美国交通工程师协会.道路通行能力手册（HCM）［M］.任福田，译.北京：建筑工业出版社，1991.

［8］姚祖康.道路与交通工程系统分析［M］.北京：人民交通出版社，1996.

［9］朱全新，舒小保.两类生灭过程的特征数及其概率意义［J］.高校应用数学学报：A 辑，2006，21（3）：311－320.

［10］王 炜，过秀成.交通工程学［M］.南京：东南大学出版社，2000.

［11］吴永欣.受公交停靠站影响的道路通行能力分析［J］.交通与运输，2010（S2）：55－58.

［12］李秀文，荣 建.快速路分、合流影响区交通特性及通行能力研究［J］.公路交通科技，2006（1）：44－48.

［13］周 伟，王秉纲.路段通行能力理论探讨［J］.交通运输工程学报，2001（2）：50－53.