沥青混合料等应变率压缩试验的时间依赖性模型＊

朱耀庭 孙 璐 朱浩然 于棋峰

（江西省交通科学研究院1） 南昌 330038） （东南大学交通学院2） 南京 210096）

沥青混合料是典型的流变材料，对时间和温度有显著的依赖性质.为研究沥青混合料的流变特性，主要采用经典粘弹塑性理论和经验模型对应力应变曲线进行描述［1－5］.由于沥青混合料力学特性和试验设备限制等因素，研究沥青混合料与时间依赖性行为一般基于蠕变试验方法，但在常低温或低应力条件下破坏阶段的出现要经过较长的蠕变时间，往往需要提高试验温度或应力水平以保证沥青混合料能够达到破坏状态，因而在特定条件下准确阐述沥青混合料流变行为和获取力学模型参数受到极大限制.本文以三轴等应变率压缩破坏试验为基础，分析沥青混合料与时间依赖性本构模型，利用相应的优化方法获取模型参数，并通过数值计算得出相应的蠕变曲线，为丰富沥青混合料与时间依赖模型和评价体系提供理论基础.

1 沥青混合料全过程力学曲线特性

等应变率压缩试验是确定材料强度的主要手段，试验获取的应力－应变全过程曲线是揭示材料力学特性的重要方法.对沥青混合料等应变率压缩试验曲线［6］研究发现，压缩试验曲线与岩石Class I破坏行为描述相一致［7］.图1为典型的沥青混合料全过程应力－应变曲线图.

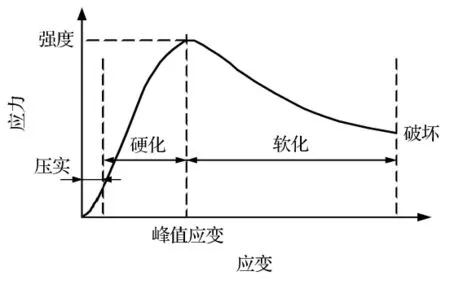
图1 沥青混合料等应变率全过程试验曲线

2 时间依赖性的可变量本构模型

应力－应变全过程曲线可通过可变量本构方程对与时间依赖特性进行表述［8－9］，其基本表达式为

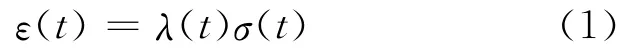
式中：ε为应变；σ为应力；λ为可变柔度，t为时间.

根据压缩试验曲线可将总的应变表示为线弹性应变ε1和非线性粘性应变ε2之和，即如图2所示的非线性Maxwell模型.建立本构模型的关键为在材料的破坏进行过程中，粘性流动呈非线性增加，且增加的速率可以表示为应力函数g（σ）和应变函数f（ε2）的乘积，即

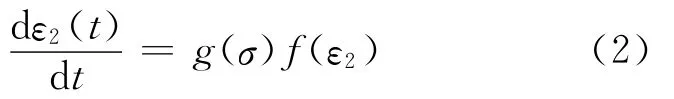
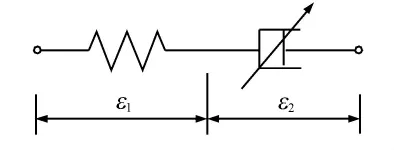
图2 非线性Maxwell模型

从临近强度破坏点时，非线性粘性应变ε2的增加起到主导作用，而在开始阶段的线弹性模量起主要作用.因此，要构建强度破坏点以后材料力学行为，必须考虑柔度的增加，假定柔度有如下关系式

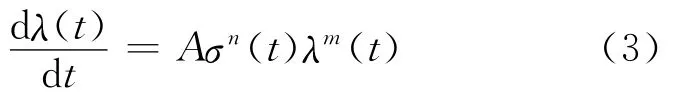
式中：A，n，m为常数.n的变化范围为n≥1；m为应力－应变曲线形状参数.可见，当n＝1时，可变模量的变化率dλ／dt与应力σ成正比，则为牛顿流体.

2.1 等应变率本构方程

在等应变率试验过程中，假定应变率˙ε＝C，C为常数，式（1）可写为

代入式（3），并考虑初值条件t＝0时，λ＝λ0，当m≠n＋1时，通过积分可推导出

将式（6）进行转化可以得出在相同柔度条件下，应力和C1／（n＋1）成正比，这可以阐述在应变率C值小时应力－应变曲线被C值大时所包裹的现象［8］.m＜0为应变硬化，m＞0为应变软化；而当m＝n＋1时，则表现为脆性破坏［10］.在m＞0时，由式（5）在dσ／dε＝0条件下可求解出强度σc的表达式为

可见，强度σc随应变率C的增加而增加，且与C1／（n＋1）成正比.

2.2 蠕变本构方程

在蠕变试验中，应力保持一定σ＝σ0，在t＝0时，σ＝σ0，λ＝λ0，ε＝ε0＝λ0σ0，当m≠n＋1时，代入式（3）推导可得

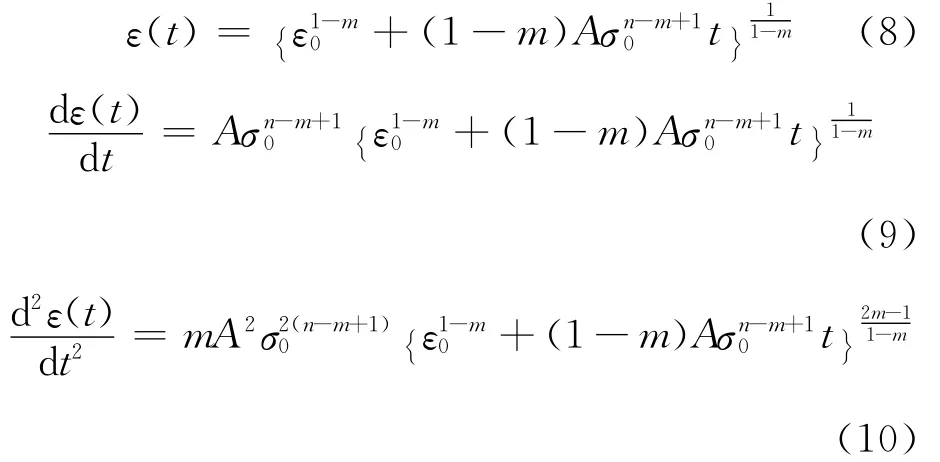
可见，在m＞1时，在一定时间范围内，蠕变方程的1次和2次导数函数是时间t的单调增加函数.文献［8］通过试验观测假定在进入第3阶段后，应变率和蠕变残存寿命tc成反比.文献［10］定义蠕变方程对时间的1次导数为0可推导出蠕变流动时间如式（11）所示.

值得指出的是，式（11）所表示的是蠕变方程在实数域内的最大值，仅存在数学上的意义，若用于实际蠕变试验描述不符合实际.根据试验数据可见，在应变达到2%～3%时，大多数沥青混合料都已达到破坏状态，因此，本文以应变2%左右时为蠕变终止时刻，探讨蠕变曲线的发展规律.

3 试验方法与沥青混合料设计

三轴等应变率压缩试验是一种经典的试验方法，能够模拟结构中材料的受力状态，与实际路面的三向受力条件相符合.试验设备采用万能材料试验系统（UTM－25），试验中将试件放在三轴压力室内，通过控制高压气体对试件施加围压，使得试件处于各向等压应力状态；激振器通过活塞施加轴向压力，在轴向产生偏应力（三轴试验见图3）.试验中以位移为控制条件，按照一定的速率施加轴向荷载，轴向偏应力随时间先逐渐增大，直至达到应力峰值后逐渐下落，此时试件已发生了剪切破坏.

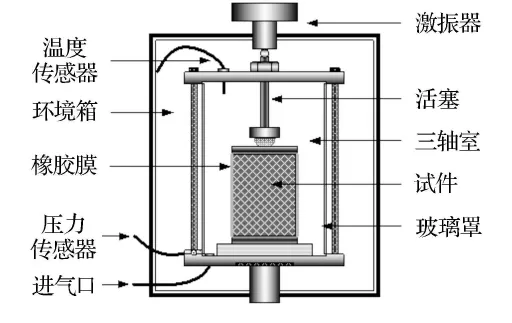
图3 沥青混合料三轴试验示意图

本文选取中面层Sup20沥青混合料作为研究对象，集料采用石灰岩，填料采用石灰岩矿粉，胶结料采用AH－70基质沥青，沥青用量为4.2%，沥青胶结料性质和混合料配合比分别见表1和图4.

表1 沥青性质

图4 Sup20级配曲线

沥青混合料的压缩强度、应力应变曲线特性与加载速率有密切关系，参考国外研究经验［11］，加载应变速率C＝1.27mm／min（0.05in／min）；为考虑中面层在车辆荷载作用下实际的侧向受力状态，通过路面力学软件计算确定围压水平为138kPa（20psi）［12］；同时为了考虑不同温度条件的影响，选取了25，40和55℃作为比较.沥青混合料试件为高150mm、直径100mm的圆柱体，经旋转压实成型后钻心而得.

4 本构模型参数获取

本构模型有A，n，m和λ0等4个未知参数，在已知试验数据的条件下，可通过本构方程获取模型参数.若通过式（1）和（3）的关系式对数据进行拟合较为简单，但涉及离散试验数据的求导问题，在试算的过程中，实际试验采集的数据由于精度和存储等因素拟合效果较差，无法确定模型参数；若直接利用式（5）和式（6）对等应变率压缩试验数据进行非线性拟合，这一方法遇到的问题是目标函数非常复杂，难以通过一般的方法获取参数，即便采用智能优化算法结果也不理想.因此，本文结合以上因素，采用2.2计算思想，先通过试算的方法得出参数的初值，再利用基于Levenberg－Marquardt（L－M）法的非线性拟合方法得出模型参数［13］.

σ（t）为试验测量数据，其函数可由离散的数据点（εi，σ（ti））（i＝1，2，…，r）给出，若要求拟合函数σ＊（ε，A，m，n，λ0）逼近试验数据σ（t），则目标函数表示Φ（A，m，n，λ0）为

L－M法则在迭代过程中对近似Hessian矩阵的牛顿法引入一个阻尼系数，若该系数值为零时即为牛顿法，而当系数值很大时，就成为较小步长的最速梯度下降法.每次迭代成功后，系数值要减少，而迭代使目标函数增加时，系数值增大，这样每次迭代后目标函数都是下降的.因此，L－M法具有收敛速度快等优点.

通过以上计算方法，本构模型的拟合曲线和模型参数见图5和表2.

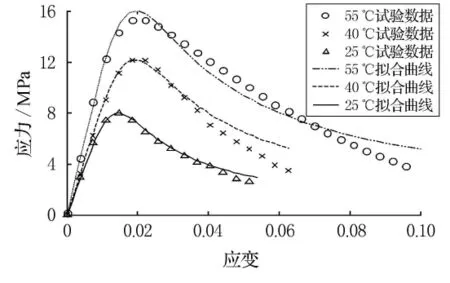
图5 试验数据拟合曲线

由于公式表达式复杂，难以直观地判断出模型各参数对结果的影响，通过实际的数值计算，可以定性地描述出模型参数的敏感性.参数λ0对破坏前的曲线斜率有决定性作用，只有取值合适才能正确地描述出破坏前材料的应力应变曲线；参数A可以一定程度上决定破坏点的取值，但必须与n，m参数大小共同作用；对曲线起至关重要作用的是参数n，m，由于这2个参数构成了指数方程，表达方式较为复杂，即使在微小变化的条件下会出现曲线突变现象，同时这两个参数决定了破坏后曲线的斜率和走势.因此，在获取参数时，对试验曲线进行试算是极为关键的，直接关系到最终的拟合效果.

表2 本构模型参数

5 计算蠕变曲线的讨论

通过等应变率压缩试验获取本构模型参数的基础上，利用式（8）可计算出在特定应力水平下沥青混合料的蠕变行为，具体的蠕变曲线如图6所示.

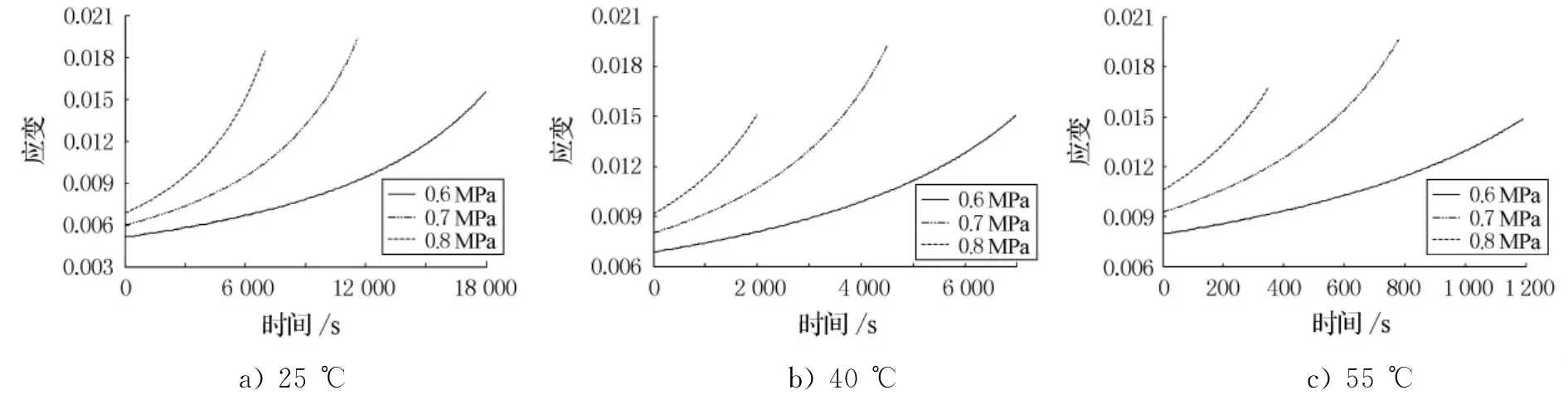
图6 不同条件下计算蠕变曲线

由图6可知，计算得出的蠕变曲线在开始一段时期内趋于线性，而后斜率逐渐增大，并最终计算结果将出现复数的情况.曲线不同阶段经历的时间与应力、温度等条件相关，在高温度和高应力条件时达到一定应变条件时所需时间较短，这与蠕变试验的结果相一致的.与经典的蠕变试验曲线相比，计算曲线可以很好地描述蠕变的第二和第三阶段，即蠕变稳定期和破坏期，且稳定期所经历的时间与温度和应力相关，随温度和应力的增加稳定期所经历的时间逐渐减少.然而，计算蠕变曲线对第一阶段即迁移期不能较好地进行表述，这是由于式（8）表达式的数学性质决定的.式（8）为一个幂函数，自变量时间t位于底数位置，时间t从0开始增加时，一定范围内蠕变斜率趋于常数，由式（9）可得，其斜率可近似地表示为

只有当时间t增加到一定阶段后，蠕变曲线的斜率才会发生巨大变化.因此，若要描述第一阶段需要对蠕变方程进行修正.

6 结 论

1）沥青混合料在等应变率压缩直至破坏的过程中，力学行为表现出与时间依赖的特性，同时破坏形式为Class I型.以粘性流动为出发点，引入等应变率非线性粘弹性本构模型，通过室内三轴试验数据进行验证表明，该模型可以对沥青混合料等应变率压缩行为进行描述.

2）可变量本构模型对沥青混合料破坏后材料力学行为有较好的描述，并可以通过模型的方程获取材料的压缩破坏强度.计算蠕变曲线能较好地阐述稳定第二阶段和破坏第三阶段蠕变曲线，但需要指出的是，本文的模型对蠕变第一阶段的描述不太明显，需要进一步的改进和提高.

［1］JUDYCKI J.Non－linear viscoelastic behaviour of conventional and modified asphaltic concrete under creep［J］.Materials and Structures，1992，25：95－101.

［2］徐世法.表征沥青及沥青混合料性能的流变学模型［J］.北京建筑工程学院学报，1991，7（1）：57－65.

［3］HOPMAN P C.Veroda：a viscoelastic multilayer computer program［J］.Transportation Research Record，1996，1539：72－80.

［4］张久鹏，黄晓明，马 涛.沥青混合料损伤蠕变特性及模型研究［J］.岩土工程学报，2008，30（12）：1867－1871.

［5］YE Y，YANG X，CHEN C.Experimental researches on visco－elastoplastic constitutive model of asphalt mastic［J］.Construction and Building Materials，2009，23：3161－3165.

［6］朱浩然.采用三轴剪切试验评价沥青混合料的抗剪性能［D］.南京：东南大学，2008.

［7］WAWERSIK W，FAIRHURST C.A study of brittle rock fracture in laboratory compression experiments［J］.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts，1970，7：561－575.

［8］大久保誠介，何昌栄，西松裕一.岩石のPost－failure Regionでの挙動－1軸圧縮応力下における時間依存性挙動［J］.日本鉱業会誌，1987，103（1189）：177－181.

［9］大久保誠介，福井勝則.岩石のコンプライアンス可変型構成方程式とそのパラメータの取得法［J］.資源と素材，2001，117（1）：13－20.

［10］金丰年，浦奎英.关于粘弹性模型的讨论［J］.岩石力学与工程学报，1995，14（4）：355－361.

［11］MONISMITH C L，VALLERGA B A.Relationship between density and stability of asphaltic paving mixtures［J］.Journal of Association of Asphalt Paving Technologist，1956，25：89－108.

［12］FOO K Y.Predicting rutting in hot mix asphalt［D］.Auburn：Auburn University，1994.

［13］MORE J J.The Levenberg－Marquardt algorithm：implement and theory［M］.Berlin：Springer－Verlag，1977.