中国航空网络鲁棒性的牵制控制研究＊

姚红光 李智忠

（同济大学交通运输工程学院1） 上海 201804） （上海工程技术大学航空运输学院2） 上海 201620）

0 引 言

航空运输易受外部干扰，因此鲁棒性的研究对于从整体上提高航空网络的可靠性，保证航空运输安全高效运营有重要意义［1］.姚红光、朱丽萍提出“最大连通子图的相对大小”可以作为航空网络鲁棒性的度量的基本指标［2］.张雯雯采用仿真方法分析航空网络鲁棒性，得出航空网络针对随机攻击有较高的鲁棒性而对蓄意攻击则比较脆弱［3］.邓贵仕等人通过建立基于总费用最低的网络优化数学模型提出了航线鲁棒性的测定方法，并进行了实证研究［4］.何春泉系统地论述了复杂网络结构对鲁棒性的影响［5］.目前，国内对与复杂网络的鲁棒性研究主要以对鲁棒性进行定量分析为主，但复杂网络鲁棒性的牵制控制最近也激起了研究者的广泛兴趣.譬如，Wang等提出了一个有效的方法使网络上所有节点都牵制控制到它的平衡点［6－7］；Chen等利用一个节点来牵制控制整个网络［8］；Zhou等利用自适应的方法来牵制整个网络［9］.赵军产等提出了通过建立代价函数达到它的最小值，以实现受控节点数与反馈增益相均衡的一种算法［10］.

本文以通过提出了“最大连通子图的相对大小”作为航线网络鲁棒性的度量标准；建立中国航空网络节点的线性耦合常微分方程；求出了最优的受控节点与反馈增益的组合，并据此确定了进行牵制控制的45座通航城市；最后通过对比，验证了牵制控制方法在提升航线网络鲁棒性中的效果.

1 中国航空网络的鲁棒性分析

1.1 数据的采集

中国航空网络的数据采集自《携程旅游网－航班时刻表》.截止到2011年5月16日，共采集到通航城市163座，国内航线2 198条，航班9 611个.以163座通航城市作为矩阵的行和列，以2城市间航班数量作为数值，形成一个163×163的中国航空网络邻接矩阵C.

1.2 航空网络鲁棒性的内涵

在航空网络中，如果某个通航城市受到突发事件影响陷入瘫痪，也就意味着同时取消了与该通航城市相连的所有的航线，从而有可能使得航空网络中其他通航城市之间的一些运输路径中断.如果在移走部分通航城市后航空网络中绝大部分节点仍是连通的，那么就称该航空网络对该通航城市的故障具有鲁棒性.

1.3 航空网络鲁棒性的度量标准

一般用“最大连通子图的相对大小s”为度量航空网络鲁棒性的指标.其计算方法如公式（1）.

“最大连通子图”包含的节点数越大表示网络连通性越好，当其与网络节点数相等时，表明所有节点间都可互联.随着陷入瘫痪的节点数f值增加，s值将不断变小.在f值一定时，s值越大，表明对网络连通鲁棒性越好.

1.4 牵制控制对提高航空网络鲁棒性的意义分析

提高航空网络的鲁棒性，有助于发现航空网络中的重要节点并进行有效保护，避免其遭受外界干扰造成延误甚至导致网络瘫痪，保证航空运输安全高效的运营.提高航空网络鲁棒性，不仅需要提高节点城市的天气应急能力、机场管理水平；更需避免因节点的耦合关系导致的网络故障的叠加与扩散.因此，提高航空网络的鲁棒性，往往需要针对网络中大量的节点进行控制与管理，代价和成本都比较高.

牵制控制，近年来被广泛应用到复杂网络的动力学控制领域，其基本思想是通过仅对网络中的一部分节点直接施加常数输入控制，而达到有效抑制整个网络的时空混沌行为的目的.对航空网络进行牵制控制可以在实现网络鲁棒性提升目标的同时，极大地减少受控节点数量，对于降低控制代价具有重要意义.

2 中国航空网络的牵制控制研究

2.1 网络节点的线性耦合常微分方程

线性耦合常微分方程是用来描述连续动力系统的重要工具.一般可以描述成下列形式：

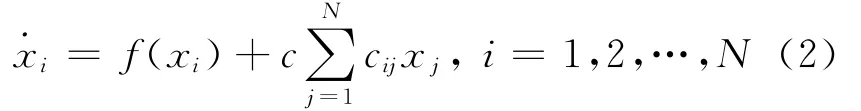
式中：N＞1，为网络中节数；f为一个连续的函数；xi为第i个节点的状态变量；c＞0是网络的耦合强度；C＝（cij）N×N为耦合矩阵，反应网络的拓扑结构其中如果节点i与节点j（i≠j）存在一个连接，那么cij＝1，否则cij＝0，C不必是对称的，但是要求其满足式（3）条件，其中ki为节点i的度.

2.2 受控节点的网络描述

将实现网络同步时的x值作为控制的平衡点：

为了将航空网络控制到上述平衡点，需要对占网络节点总数的比例为σ（0＜σ＜1）的小部分节点实施牵扯控制.假设选择节点i1，i2，…，ir作为被牵扯控制的节点，r表示受牵扯控制的节点数量.在线性反馈作用下，节点的牵制网络可以被描述如式（4）.

式中：eik为受控的节点在实现正常机场功能情况下的代价，即机场硬件设施的总投资及运营费用；d＞0为反馈控制增益系数；de ik为反馈增益.在航空网络中，反馈控制增益的现实意义是：各节点机场为在“气象因素”、“流量突增”、“设施故障”等突发影响发生时，仍能保持机场的正常功能而做的额外准备所付出的代价.这种额外准备不仅包括机场在硬件条件、基础设施上的升级、改进和储备，也包括管理手段、运作流程的优化，由于机场的硬件投入及运营成本巨大，因此这种额外准备代价巨大.

2.3 受控节点数r与反馈控制增益系数的均衡

在传统的牵制控制研究中，为了使动力网络稳定到事先确定的平衡点上，通常将反馈控制增益系数d设为足够大；然而，要求d值足够大在现实情况下是不可行的；当d＝1时，则为预防突发影响储备的运力与机场现有运力相等，即意味着额外运力储备的成本与整个机场建设的总投资相同，在现实中是不行的；只有将d值控制在一个足够小的水平上，对航空网络的牵制控制才有现实意义.

若对于某个ε0＞0，存在一个自然数r∈［1，N－1］，和一个反馈增益系数d满足式（5），则受牵制网络（式4）可以稳定到均衡点上.

式中：λi为矩阵＋）／2的Mi最大特征值；Mi为同时去除矩阵（＾C＋＾CT）／2的第1，2，…，N－1行和列得到的矩阵，并且是矩阵C的主对角元素cii被［λmin（p）／λmax（p）］cii取代后 得到的 矩阵.D，D＝diag（d，…，d），是一个正定11n的对角矩阵.

假设＾λi是矩阵（＋）／2－D／λmax（P）的最大特征值，如果令＾λ1＝λr＋1，则反馈增益d值不得不达到足够大，这是不切合实际的；因此，引入一个松弛因子ε0，使得对于一个适当的d，＾λ1≤λr＋1＋ε0成立.牵制节点越多，满足上述不等式所需的反馈增益d就越小.对于一个确定的牵制节点数目r，反馈增益系数d存在着一个临界值，当d大于这个临界值时，航空网络中受控节点的牵制网络就能达到稳定的平衡点.同样，对于一个给定的反馈增益d，牵制节点的数目也存在着一个临界值，达不到这个值，受控节点的牵制网络是不能到达指数稳定的状态.因此，可以得到一系列可行的组合（r，d），它定义了一个稳定的区域，用它可以划分牵制节点数目r和反馈增益d的稳定的参数空间.

建立代价函数Q（r，d）＝rαd1－α，可以得到是函数值取得最小值的（r，d）的可行组合，从而兼顾二者的取值.

2.4 中国航空网络牵制控制的实证分析

从航空网络鲁棒性分析的角度上看，节点机场包括“正常”与“瘫痪”2种状态.以各航班在机场内平均等待服务时间为标准，运用排队论原理，可以得出中国航空网络节点的线性耦合常微分方程为

将实现节点机场的正常功能为控制均衡点，按式（4）建立中国航空网络节点的牵制网络方程.并利用赵军产等在文献［10］中提出的算法：先确定网络的最小耦合强度与最少牵制节点后，然后不断增加牵制节点，最终选择一个合适的α，使代价函数Q（r，d）达到它的最小值，进而得到最优的（r，d）组合，计算出中国航空网络的受控点数量与反馈增益系数的可行组合情况（r，d），见表1.

表1 部分可行组合表

当α在［0，1］之间取不同值时，对于上述可行组合Q（r，d）＝rαd1－α值，变化情况如图1所示.

图1 α＝0，0.1，0.2，…，1时可行组合对应的Q值

通过计算可知，当α＝0.5时同时兼顾了r，d的取值，此时当r＝45时，Q 有最小值min（Qα＝0.5，R＝45）＝20.784 61.即对于中国航空网络，只要有选择的控制45个关键节点，就能够以储备受控节点9.6%的服务能力为代价，实现对整个网络的有效控制.

3 牵制控制对中国航空网络鲁棒性的影响分析

3.1 45个受控节点分析

由于在中国航空网络节点的线性耦合常微分方程中，以“度”的平均值来反映航空网络的耦合强度，因此从对航空网络鲁棒性影响的角度考虑，应选择度排序在前45位的城市作为牵制控制的对象.

在网络中，节点i的度ki定义为与节点i相接的边的总数.在航空网络，一个通航城市的度越大就意味着与其相连的城市数越多，其拥有的航线数也就越多.应用大型网络分析软件Ucinet，以及采集到的163×163的中国航空网络邻接矩阵C，计算出中国163个通航城市的度，排名前45位的通航城市如表2所列.这45座节点城市共拥有航线1 767条，占全部航线数量的80.39%，形成了中国航空网络的核心.

表3 前45位通航城市度值表

3.2 航空网络牵制控制与随机控制的鲁棒性对比分析

牵制控制可以以较低的代价保证航空网络的服务功能，相比随机控制可以大幅度提高航空网络的鲁棒性.选择表2所列的45个城市作为受控对象进行牵制控制，与随机选择的45座城市进行航空网络受攻击状态下的鲁棒性对比分析.其研究步骤是：（1）确定受控城市及其数量，使其免于陷入瘫痪状态，即保证其拥有航线的有效性；（2）对航空网络中的非受控城市进行模拟攻击，中断其所有航线，即令航空网络邻接矩阵C中其对应的行与列中所有元素值为零，并形成新的航空网络邻接矩阵R；（3）通过计算新矩阵R的鲁棒性s值；（4）在新的航空网络邻接矩阵R上重复上述步骤，不断增加被攻击的城市数量，分析其变化 的变化趋势，直到除受控城市外地所有城市都受到攻击.

按上述步骤，牵制控制与4次随机控制的s值对比如图2所示.

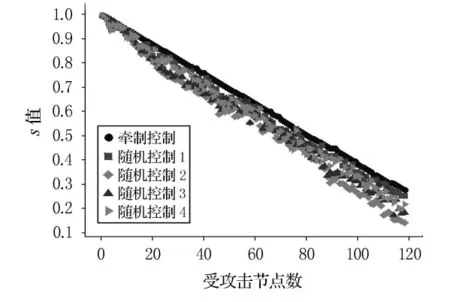
图2 受攻击下的牵制控制与4次随机控制的s值对比图

从图2可以看出，在受攻击节点在由1向最大值118变化时，牵制控制的s值始终大于随机控制的s值；在s值相同时，牵制控制的受攻击节点数始终大于随机控制.表明，相比随机控制，牵制控制可以有效的提高航空网络的鲁棒性.

4 结 论

1）提高航空网络的鲁棒性，对于保证安全高效的航空运输有重要意义.牵制控制相比于其他控制方式可以在代价相同的条件下，保证航空网络较高的鲁棒性.

2）针对中国现有的航空网络，以9.6%的反馈增益，对北京、广州、上海等45座城市进行牵制控制，是兼顾了受控节点数与反馈增益的较为合理的方案.

后续研究应在“考虑通畅、拥堵、瘫痪等多种网络状态”基础上完善模型参数及场微分方程.

［1］刘宏鲲.中国航空网络的结构及其影响因素分析［D］.成都：西南交通大学，2007.

［2］姚红光，朱丽萍.基于仿真分析的中国航空网络鲁棒性研究［J］.武汉理工大学学报：交通科学与工程版，2012，36（1）：42－46.

［3］邓贵仕，武佩剑，田 炜.全球航运网络鲁棒性和脆弱性研究［J］.大连理工大学学报，2008，48（5）：765－768.

［4］张雯雯.复杂网络理论在航空网络中的应用研究［D］.北京：中国民航大学，2009.

［5］何春泉.关于复杂网络演化过程中鲁棒性的研究［D］.上海：上海交通大学，2009.

［6］WANG X F，CHEN G.Pinning control of scale－free dynamical networks［J］.Phys A，2002，310：281－302.

［7］LI X，WANG X F，CHEN G.Pinning a complex dynamical network to its equilibrium［J］.IEEE Trans Circ Syst－I，2004，51：2074－2087.

［8］CHEN T，LIU X，LU W.Pinning complex networks by a single controller［J］.IEEE Trans Circ Syst－I，2007，54：1317－1326.

［9］ZHOU J.Pinning adaptive synchronization of a general complex dynamical network［J］.Automatica，2008，44：996－1003.

［10］赵军产，陆君安，吴晓群.一般复杂动力网络的优化牵制控制［J］.中国科学：信息科学，2010（6）：821－830.