GPS信息和限误差信息率与信息率失真及复杂性失真之间的关系

鲁晨光

（广东方舟投资管理有限公司,广东广州 510610）

0 引言

文献[1]介绍了如何推广Shannon信息论[2]到一般领域,包括语义信息和感觉信息领域。书中介绍信息率失真的两个新版本:限误差信息率 R（AJ）（文中记为R（T））和保精度信息率R（G）,讨论了它们和信息率失真之间的等价关系。后来又进一步讨论这些问题[3-4]。现在,通过研究发现复杂性失真只是限误差信息率的特例,复杂性理论研究者肯定的复杂性失真和信息率失真之间的一般等价关系是不成立的。文献[1]同时介绍了如何根据人眼色觉分辨率度量色觉信息,目前,GPS提供信息以类似的方式;并且通过对GPS信息的度量,可以加深对信息率失真的理解。文中首先介绍如何度量GPS提供的信息,然后讨论和数据压缩理论相关的那些函数的等价关系,并用编码例子说明。

1 GPS信息——从统计信息到预测信息

1.1 GPS精度和集合Bayes公式

全球定位系统（Global Positioning System,GPS）通常假设目标实际位置以GPS读数为中心正态分布。

假设信源是带有GPS跟踪器的被盗小车,为简化起见,其位置用一维离散随机变量X表示,实际可能位置是x1,x2,…它们构成集合 A={x1,x2,…}。用Y表示GPS读数,Y的实际取值是y1,y2,…;它构成集合B={y1,y2,…}。读数 yj即xj的估计,通常写为＾xj。那么在信源等概率假设下,读数 yj出现时,xi发生的条件概率分布为:

其分布如图1所示。GPS精度常见的表示法是均方根差（Root Mean Square error,RMS）表示法。DRMS=10米就表示σ=10m,目标有68.2%的可能性在以读数xj为中心,半径10m的圆圈之类。2DRMS=10m就表示2σ=10m,目标有95.44%的可能在半径为10米的圆圈之类。常见的还有一种是圆概率误差（CEP）表示法,CEP是10m,就表示实际位置有50%可能落在以GPS读数为中心半径=10m的圆圈之内。

请注意,一般情况下,P（X）不是等概率的,条件概率P（X|yj）也不会呈正态分布。比如,汽车在公路上的先验概率比较大,即使GPS定位小车在公路附近农田里,那也并不意味着汽车在农田里概率最大。要表示GPS独立于信源的特性,最好被写为

把上面曲线理解为 xi和xj混淆概率函数或xi和xj的相似度,其最大值等于1。而条件概率P（xi|yj）对 xi求和等于1,对于连续分布其最大值是0.399/σ。

混淆概率可以来自随机集合的统计[7-8]。假设做很多次分辨实验,每次确定一个A中子集,其中元素和 xj想混淆。做N次实验就得到N个子集,它们的左右边界可能不同,如果有Ni个子集包含xi,那么混淆概率就等于:

定义模糊糊集合[9]Aj={所有和 xj相混淆的xi},那么 xi在Aj上隶属度,记为 Q（Aj|xi）,就可以用混淆概率c（xi,xj）来定义,即 Q（Aj|xi）=c（xi,xj）。

Q（Aj|xi）也可以被理解为 xi和xj的相似度,或命题yj=“X is about xj”在 xi发生时的逻辑真值或yj的后验逻辑概率。而yj的先验逻辑概率就是Q（Aj|xi）的平均值:

也就是Zedah曾提出的模糊事件的概率[10]。已知X在Aj中,求X的概率分布,有集合Bayesian公式[4]或广义Bayesian公式[8]:

后面讨论信息率失真函数和限误差信息率函数时,将看到,上面关于Q（Aj）和P（xi|Aj）的公式一再出现。当Aj是清晰集合时,P（xi|Aj）的图解如图3所示。

图1 反映X和xj的混淆概率和相似度的GPS的误差函数

图2 预言信息公式图解

1.2 从统计信息到预言信息

要度量一个GPS读数提供的信息,用Shannon熵 H（X）公式或Shannon互信息 I（X;Y）公式都是不行的。因为它们是用来度量平均信息的[2]。为此,提出用Shannon互信息公式中的对数部分度量单个事件提供的信息[11],公式是:

但是这个公式能导致负的信息（当P（xi|yj）＜（P（xi）时）,所以很多人对此有疑问。

接受这个公式,是因为负信息可以理解为因谎言或错误预测而增加的编码长度。但是,度量GPS信息还要考虑事实检验,因为根据常识,定位准确信息就多,定位不准信息就少,甚至是负的。且称GPS信息是预言信息,而Shannon信息是统计信息。

把经典信息公式（6）中的条件”yj”改为“yj为真”,即用 xi∈Aj取代yj,那么公式（4）就变为:

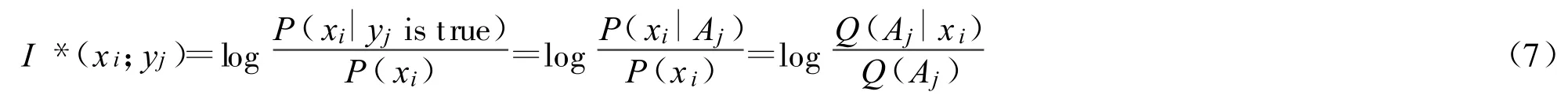
注意:除了需要先验预测P（X）和真值函 Q（Aj|X）,还需要用以检验的事实X=xi。

由图3可见,事实和预测完全一致时,即 xi=xj,信息量最大;随着误差增大,信息量渐渐变小;误差大到一定程度信息就是负的。这是符合常理的。Q（Aj）越小,信息量越大。有两个因素决定Q（Aj）大小,一是预测精度,即 σ,它越小,Q（Aj）就越小;二是 Q（Aj|xi）覆盖区域的 P（xi）大小,P（xi）越小,Q（Aj）就越小。这样就有结论:预测精度越高,或者事件越是出乎意外,信息的绝对值就越大。同时犯错误的可能性也越大,检验也就越严峻。如果经得起检验,即Q（Aj|xi）较大,信息量就越大。这一公式非常符合Popper关于科学理论进步的信息准则[12]。

1.3 理想GPS和普遍必然命题的信息

假设有理想GPS,被定义为:

（1）混淆概率仅取0,1二值;

（2）声称实际目标100%落在指定范围内。

一个可能的混淆概率函数如图2中的矩形所示。信息量公式变成

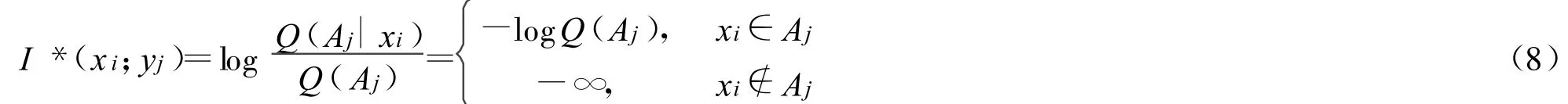
其图解如图3所示。

不难证明,只要有一个xi不在Aj中,求得的平均信息都是-∞。信息负无穷大就意味着:按照语义为分布是P（X|Aj）的信源编码时,只要有一个 xi不在Aj中,则编码长度无论多大,都会失败。

根据Popper理论,对于普遍必然命题,只要有一个反例,该命题就被证伪了[12]。上面公式正好反映Popper的这一思想。根据公式,对于永真命题和永假命题,或者永远半真半假的命题,都有 Q（Aj|xi）/Q（Aj）=1,所以信息量都是0。这和Popper理论一致。

日常语言中,由于接收信息者总是假定有意外事件的可能,或者说按模糊方式理解所有命题,负无穷大信息极少发生。

图3 理想GPS和普遍必然命题提供的信息

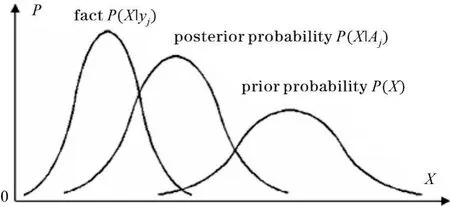
图4 图解广义Kullback公式

1.4 广义Kullback公式及其用于预测优化

如何求yj提供关于X的平均信息,开始采用Kullback公式:

这里假设P（X|Y）=P（X|Y是真的）,即对于所有 xi,P（xi|yj）=P（xi|Aj）。但是实际上,两者未必相同。后来发现,保留对数左边的条件概率,采用公式

反而使公式更有解释力。这是非常重要的一步,因为这样就能反映信息来自事实检验。这就是广义Kullback公式。这里,P（xi|yj）就是证据,而P（xi|Aj）是理论预测,P（xi）是先验知识。Theil曾经提出的信息差公式与此类似[13],但是上面公式含义更丰富。

可以把-logP（xi）理解为原先为P（X）按最优式编码时 xi的码长,-log P（xi|Aj）理解为yj出现后为P（xi|Aj）按最优方式编码时 xi的码长。这样,I（X;yj）就是因预测yj而节省的平均码长。

图4表明,理论预测P（X|Aj）越接近事实P（X|yj）,信息量越大,最大值就是Kullback信息;信源或先验估计P（X）越与事实P（X|yj）不同（表示预测的事情越是出乎意外）,信息量越大。

现在假设X是经济指标,用两个参数 xj和σj预测经济指标,即逻辑条件概率是

上面广义Kullback公式就可以用于预测的评价和优化。

设z是某种客观因素,＜yj,σj＞表示一种预测,被预测的经济指标的条件概率是P（X|z）。选择哪个预测＜yj,σj＞最好 ,改变 ＜yj,σj＞,使广义 Kullback 信息

达最大的＜yj,σj＞就最好。对于GPS精度 σ和读数yj的选择,上面公式同样适用。

如果预测经常不准,或者发信人有意说谎,收信人可以总结经验,修改语义,比如令

这样将能使实际收到的信息接近统计信息。

1.5 广义互信息公式

对I（X;yj）求平均,得到广义互信息公式:

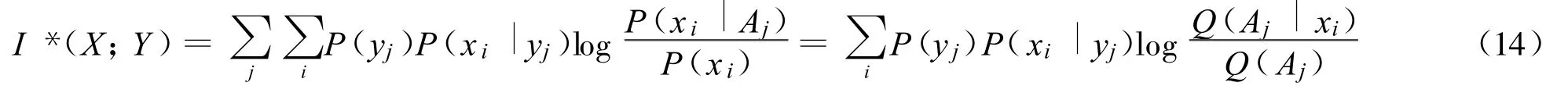
当预测和事实一致时,I*（X;Y）可以写成

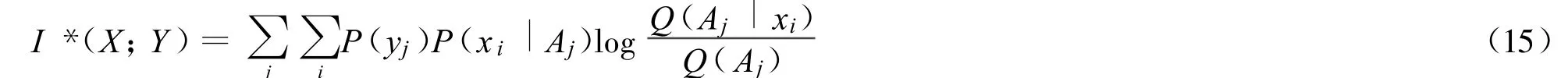
从上面公式可见,Shannon广义互信息是广义互信息在预测总是和事实一致时的特例。它也反映节省的平均码长。Shannon互信息可以理解为通信成本,而广义互信息可以理解为通信的效用,其上限是Shannon互信息。

2 限误差信息率及其和信息率失真及复杂性失真之间的等价关系

2.1 从信息率失真到复杂性失真

在为声音、视频、经济、地理位置…数据编码时,适当的有失真编码将大大提高通信效率。为此Shannon提出Rate distortion理论[2],并且得到T.Berger等[14-15]的大力发展。

假设为数字X编码,设离散随机变量X∈A={x1,x2,…}和Y∈B={y1,y2,…}分别表示源码和目的码,信源是前后无关的。假设yj和xi之间的失真是dij=d（xi,yj）,那么它的平均值就是

给定离散无记忆信源P（X）和E（dij）的上限D,改变P（Y|X）,求Shannon互信息的最小值:

R（D）就是信息率失真函数。Shannon证明了,它反映为每个数字编码的最短平均码长（通过分组编码实现）或最小信息速率（忽略两者之间的微小差别）。

有些文献[15]区分了率失真函数和信息率失真函数,前者是可操作性定义,考虑分组编码和解码;后者是信息定义,只考虑由信源到信宿的编码。两者被证明是等价的。据此,文中只考虑信息率失真函数,不考虑分组编码——其结论应该和考虑分组编码和解码时的结论同样。

然而,数据压缩实践中,需要对每对（xi,yj）之间的误差给出限制。Kolmogorov提出基于其复杂性理论的结构函数[5],最近又有人提出复杂性失真[6]。复杂性理论把一个字符串的最短编码长度叫做这个字符串的复杂性。有失真编码时,如果

成立,则对于每个xi,集合B上存在一个以yi为中心的失真球Bi,用球中任何一个yj表示xi都可以。同时对于任何yj,A上存在一个以xj为中心失真球Aj,yj可以是Aj中任何一个xi的代表。球的半径都是D0.5c 。给定信源和失真球限制,可求出最小平均码长或Shannon互信息（忽略微小误差）,设为 C,它是Dc的函数,即C=C（Dc）。它就是复杂性失真函数[6]。采用同样的编码,假设对于每个yj,失真球Aj中元素一样多,为S=|Aj|,hx（Dc）=logS就是结构函数。

也需要不同尺寸的容差集合或容差球,用以限制编码误差。比如,随着颜色的明度增加,人眼对色差的敏感性减弱,这意味着,对于较暗的颜色,需要较小的容差,对于较亮的颜色,需要较大的容差。

2.2 定义限误差信息率并证明复杂性失真是其特例

设AXB上存在相似关系,xi和yj之间的相似度是cij=c（xi,yj）=c（xi,xj）∈[0,1],如式（2）所示。对于每个xi,B上存在一个容差集合Bi,yj在Bi上的隶属度是cij。对于每个yj,A上存在一个容差集合Aj,xi在Aj上的隶属度也是cij。这也就是说,这些容差集合可以是模糊的,并且有

如果对于每个Bi,

称一组集合 T={B1,B2,…}是对 xi,x2,…的编码的容差。如果 B1,B2,…是清晰集合,即cij∈{0,1},上面限制变成

现在,在允许选择和 xi相似的yj代表xi时,给定 P（X）和 T,改变 P（Y|X）,求最小信息速率 R（T）,

就是限误差信息率。很显然,当B1,B2,…是分别以y1,y2为中心的大小一样的球或区域,R（T）就变成C（Dc）。所以C（Dc）是R（T）的特例。

假设B1,B2,…是清晰集合时,看R（T）和R（D）之间的等价关系。

现在考虑函数R（D）。把 xi和yj之间的失真定义为:

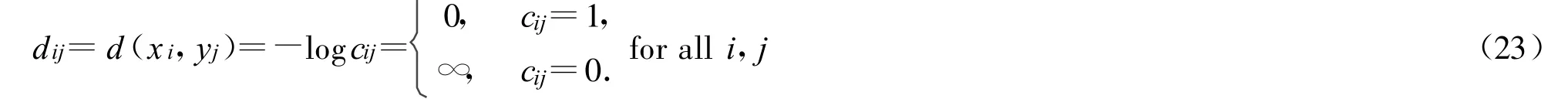
根据式（21）和式（23）,限制 E（dij）≤D=0和限制 T等价,即 R（D=0）=R（T）。所以 C（Dc）也是 R（D）的特例。

2.3 反映信息率失真和复杂性失真之间等价关系的广义熵

下面证明,当 T是一组清晰集合时,R（D=0）等于一个广义熵。

知道,Rate-distortion函数的参数表示[16]:

其中

令s=-1/（2σ2）,可以看出GPS信息和信息率失真之间的清晰联系。这样就可认为exp（sdij）=Q（Bi|yj）,λi=1/Q（Bi）,于是得到和（15）相似的公式:

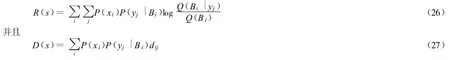
当T是一组清晰集合时,exp（-∞）=0,exp（0）=1,D=0时,R和s无关。于是有

虽然Q（Bi）是P（Y）的函数,但是并不是任何一个 H*（X）都等于一个R（D）。改变P（Y）使得 H*（X）达最小,设为 HP（Y）*（X）,它才等于 R（D=0）:

所以 R（T）=R（D=0）=HP（Y）*（X）。

仅当所有Bi大小一样呈球形时,才有C（Dc）=R（T）=R（D=0）。

给定 T时X的条件熵是

如果在每个失真球 Aj中元素相等,为S=|Aj|,并且等概率发生,H（X|T）就变成结构函数hx（Dc）。

一般情况下,结论C（Dc）=R（Dc）[6]是不对的。肯定失真-信息率和期望的结构函数之间有一般等价关系[5],也是不对的。因为在复杂性理论中,那些容差球是清晰集合,而在信息率失真理论中,那些容差球是模糊集合,后者较前者限制更松。下面用编码例子说明它们的差别。

2.4 用一个编译码例子说明R（Dc）＜C（Dc）

这个例子也将显示如何改变P（Y|X）从而减少I（X;Y）的思路。

Example:A={1,2,3,4},B=（1,2,3,4）,允许误差|X-Y|≤1。给定P（X）,通过适当的编码得到R。

实际的数据压缩过程是:P（X）→信源编码→存储和传输→解码→P（Y）,这里不考虑中间环节（中间可能要采用分组码）,只考虑用怎样的编码即P（Y|X）可以减少I（X;Y）得到 R。

由（28）式知,对于每个xi,逻辑概率Q（Bi）越大越好;不同的Bi之间相互越重叠越好。这样条件熵H（X|Y）就较大,信息I（X;Y）=H（X）-H（X|Y）就较小。

如果简单用y2表示 x1和 x2;用 y3表示x3和x4,平均信息量是1比特。参看式（25）和式（28）,采用优化方法给信源编码。让X=1时,Y=2;X=4时,Y=3;X=2或3时,Y=2或3,随机产生。这样,就有表1数据。

表1 为C（Dc=1）寻找P（Y|X）

注意,Q（B2）=Q（B3）=1,所以X=2或3时,传递信息是0。有 R（T）=C（Dc）=-0.25log0.5-0.25log0.5=0.5比特。

但是,这时候E（dij）=0.75＜1。下面编码可以证明R（Dc）＜C（Dc）。

现在令 dij=（yj-xi）2,求 E（dij）≤D=Dc=1时的R。令 s=-0.45,y2=y3=0.5,Q（Ai|yj）=exp[s（yj-xi）2],P（yj|xi）=P（yj|Ai）,于是有表2数据。

表2 为 R（D=1）寻找P（Y|X）

那么,根据式（24）,有 D=0.994,R（D）=sD+H*（X）=-0.447+0.816=0.369比特。

可见,一般情况下R（Dc）＜C（Dc）。

2.5 限误差信息率和信息率失真之间的等价关系

假设 T={B1,B2,…}是一组模糊集合,Shannon互信息是I（X;Y）=H（Y）-H（Y|X）。当容差限制是 T或不等式（20）时,下式成立时:

P（Y|X）最分散,所以H（Y|X）最大。这个等式对于R是必要的,但不是充分的。改变P（Y）使 I（X;Y）达到最小值,就得到限误差信息率函数:

假设 Q（Bi|yi）=exp（sdij）for all i,j,参看2.3节,得到 R（T）==R（D）。这意味着 R（D）函数是 R（T）函数在 Q（Bi|yj）=exp（sdij）for all i,j时的特例。其中 s就反映预测的精度,s越大,所需要的信息速率就越大。

显然,广义信息测度和R（D）函数之间存在深刻联系,它们都和误差及语义密切相关。

3 结束语

以GPS为例,推广经典信息公式到广义信息公式,讨论限误差信息率和信息率失真怎样和广义互信息公式相联系,证明了信息率失真 R（D）是限误差信息率R（T）的特例,而复杂性失真C（Dc）是信息率失真 R（D）的特例。

致谢:感谢汪培庄教授和吴伟陵教授的支持和鼓励

[1] 鲁晨光,广义信息论[M].北京:中国科技大学出版社,1993.

[2] C E Shannon.A mathematical theory of communication[J].Bell System Technical Journal,1948,27:379-429,623-656.

[3] 鲁晨光,广义互熵和广义互信息的编码意义[J].通信学报,1994,15（6）:37-44.

[4] C Lu.A generalization of Shannon's information theory[J].Int.J.of General Systems,1999,28（6）:453-490.

[5] P D Grunwald,P B Vitany.Kolmogorov Complexity and Information Theory With an Interpretation in Terms of Questions and Answers[J].Journal of Logic,Language and Information,2003:497-529.

[6] D M Sow.Complexity Distortion Theory[J].IEEE T ransactions on Information Theory,2003,49（3）:604-609.

[7] P Z Wang.Random sets in Fuzzy Set theory[A].System&Control Encyclopedia,edited by M.G.Singh,Pergamon Press,1987:3945-3947.

[8] J B Tenenbaum,T L Griffiths.Generalization,similarity,and Bayesian inference[J].Behavioral and Brain Science,2001,24（4）:629-640.

[9] L A Zadeh.Fuzzy sets[J].Infor.Contr.,1965,18:338-353.

[10] L A Zadeh.Probability measures of fuzzy events[J].Journal of mathematical Analyses andApplications.1968,23:421-427.

[11] S Kullback.Information and Statistics[M].New York:John Wiley&Sons Inc.,1959.

[12] K R Popper.Conjectures and Refutations:The Growth of Scientific Knowledge[M].New York:Harper&Row,Publishers,1968.

[13] H Theil.Economics and Information Theory[M].North-Holland,Amsterdam,1967.

[14] T Berger.Rate Distortion Theory:A Mathematical Basis for Data Compression,Englewood Cliffs[M].NJ:Prentice-Hall,1971.

[15] T M Cover,J A Thomas.信息论基础[M].北京:机械工业出版社,2008.

[16] 周炯盘.信息理论基础[M].北京:人民邮电出版社,1983.