徐变对大跨度预应力混凝土连续箱梁桥施工线形控制的影响*

张汉一，周凌宇，贺桂超，肖金敏，3

(1.中南大学土木工程学院，湖南长沙 410075;2.中铁四局，江苏苏州 215131;3.长沙市建筑工程安全监察站，湖南长沙 410016)

徐变是混凝土本身固有特性，会导致混凝土结构受力和变形随时间而改变，对结构的受力性能及长期变形影响很大。从1907年Hatt首先发现混凝土徐变至今，国内外一大批学者对其开展研究工作，虽已取得了一些重要成果，但由于混凝土徐变机理及影响因素十分复杂，对混凝土徐变现象还没有完全被掌握［1］。目前对于混凝土徐变分析主要依据徐变预测模型，应用较多的有GL2000模型［2］、ACI－ 209R 模型［3］、AASHTO 模型［4］、BS5400 模型［5］及我国的 JTJ 023 －85 模型［6］和 JTG D62 －2004模型［7］。这些模型都是建立在相应试验数据基础上，由于各模型考虑影响因素不同，因此，每种模型的计算精度及适用性也存在差异。采用悬臂施工的连续梁桥，由于结构体系转换，前期结构产生的徐变变形受到后期结构的约束，将在结构中产生徐变次内力和支座次反力［8］。大跨度预应力混凝土连续梁桥上部结构在使用期间的主要病害表现在2个方面:一是箱梁主跨跨中下挠过大，二是箱梁梁体开裂。而这导致这2方面的主要原因是有效预应力的损失和对混凝土徐变效应的估计不足［9］。由于大跨度桥梁施工周期长，徐变效应影响大，就需要在施工过程中通过施工控制，调整模版标高以及合理设置预拱度来抵消施工期间徐变引起的挠度，保证桥梁达到设计线形。本文以京沪高铁跨秦淮新河特大桥为工程背景，探讨施工控制中徐变效应的计算分析方法，以便为今后同类型桥梁施工提供参考。

1 混凝土徐变效应分析

随着我国高速铁路的快速发展，对高速铁路上桥梁的要求也越来越高，因此分析混凝土徐变的影响，对桥梁结构的安全及适用性具有重要影响。

对混凝土徐变的计算，关键问题是如何确定混凝土徐变系数。由于混凝土徐变机理的复杂性，目前还没有1个通用的计算公式，国际上主要通过预测模型来计算徐变系数。但由于每个预测模型考虑的因素不同，因此计算结果也存在一定差异，通过对比各个预测模型，发现各预测模型所考虑的参数主要集中在水泥类型、计算龄期、加载龄期、混凝土受荷、混凝土构件的截面尺寸和形状、环境相对湿度等因素上。本文以目前高速铁路桥梁常用C50混凝土为研究对象，对混凝土徐变效应进行分析，各预测模型所采用的主要参数见表1。

根据表1中参数，计算得到国内外主要的混凝土徐变预测模型的徐变系数10年的变化曲线如图1所示。

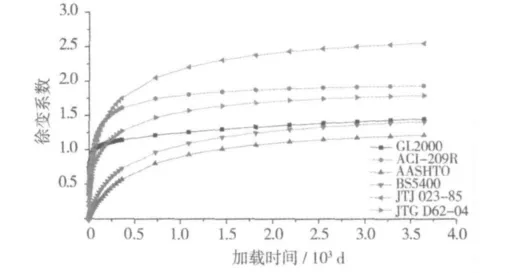
图1 C50混凝土加载10年过程徐变系数变化曲线Fig.1 The creep coefficient curves of C50 concrete load 10－year

从图1可以看出:各模型计算出的徐变系数大致可以分为4个水准;加载10 a后，85规范计算的终极徐变系数最大，为2.562;ACI－209R模型与04规范计算的终极徐变系数中等，分别为1.942和1.803;GL2000模型和BS5400模型计算得到的终极徐变系数次之，分别为1.458和1.418;AASHTO模型计算得到终极徐变系数最小，为1.221。各模型计算的徐变系数在10 a以后增长缓慢，且数值增长较小，徐变在3 a内基本完成总徐变的95%。

混凝土徐变效应进行21 d，51 d和1 a后，徐变系数与终极系数的比值如表2所示。

表1 C50混凝土各预测模型主要参数Table 1 The main parameters of the forecasting model of the C50 concrete

表2 各预测模型计算徐变系数与终极徐变系数的比值Table 2 The ratio between calculate creep coefficient with ultimate creep coefficient of the prediction model

对比图1和表2可以看出:AASHTO和BS5400规范计算出的徐变系数前期发展速度极为缓慢，在加载21 d时，预测的徐变发展程度与国内实际试验差距较大［10］。ACI－209R规范、85规范和04规范计算的徐变系数在前期发展适中，但是，其计算值仍然偏小，GL2000预测模型计算出的徐变系数在前期与试验值较吻合。高性能混凝土加载初期徐变发展速度较快，特别是对早龄期加载而言，该规律最为突出，GL2000预测模型很好地显示了该特征。

普通混凝土的徐变系数为2～4，而高性能混凝土的徐变系为1.8～2.4，试验研究表明，高性能混凝土的徐变系数都远远小于同强度等级的普通混凝土。这主要是由于粉煤灰和矿粉可以使混凝土中产生徐变变形的主体(水泥石)的基本徐变显著降低，使混凝土的级配更加完美，混凝土骨架结构更加密实牢固。

通过对比文献［11］中给出的试验数据与曲线，ACI－209R规范和04规范计算出的混凝土中后期徐变系数与试验结果吻合较合理。

2 算例分析

在具体工程实践中，往往会运用有限元对主要受力结构建立有限元分析模型。为了验算计算效果，具体分析说明徐变系数与混凝土梁桥的挠度的关系，将使用Midas软件建立模型，按不同的规范或计算式计算徐变对梁体挠度的影响。箱梁截面尺寸及有限元模型如图2和图3所示。

在模型中取年平均环境湿度为70%，混凝土立方体抗压强度取为50 MPa，混凝土开始加载龄期取为7 d，混凝土加载龄期和构件理论厚度根据计算取为185 mm。

各徐变预测模型或公式的计算结果对比如图4所示。由于所建模型为对称结构，在作图过程中只给出了梁体一半单元的挠度。

图2 箱梁截面尺寸Fig.2 Cross－ section dimension of box girder

图3 箱梁模型简图Fig.3 The model diagram of box girder

由实际计算结果可以看出:由徐变效应引起的上挠位移与所采用的徐变预测模型直接相关。《公路桥涵通用图》中关于预制梁反拱度设置为18 mm的要求，可以判断04规范与ACI－209R规范较好地吻合了这一要求。与前述的各预测模型性质相同，85规范只是粗略计算，在计算方法上高估了挠度的变化，不能够很好地适用于目前的工程实际;GL2000预测模型前期较吻合，在使用阶段后期，徐变效应预测值稍小。进行前期预测时，可以借鉴GL2000预测模型的结果;而做长期预测时，04规范与ACI－209R规范预测值较为合理。04规范计算值介于GL2000预测模型和ACI－209R规范计算值之间，体现了04规范在实际工程计算中的合理性。

分析表明对于处于弹性阶段的梁体，徐变引起的挠度与荷载引起的挠度呈线性关系。随着时间的推移，混凝土徐变引起的挠度在预应力弹性挠度的基础上进一步发展，其方向与预应力产生的弹性反拱方向一致。在时间3 a的徐变效应下，各单元的徐变挠度与预应力荷载挠度的比值相对稳定。

3 徐变在京沪高铁跨秦淮河特大桥中的控制应用

3.1 桥梁概况

京沪高速跨秦淮新河特大铁路桥为三跨一联连续梁，本桥梁上部结构为60 m+100 m+60 m变高度预应力混凝土连续箱梁，中支点处支座中心线与线路法线夹角为40°，上部结构采用单箱单室截面箱型梁，主桥立面图如图5所示。

由于通航要求，施工安全成为施工重点，该桥梁设计中采用悬臂浇注法施工，每个“T”构纵桥向划分为13个悬臂梁段，从根部至跨中分别为2×2.50 m，1 ×2.75 m，3 ×3.00 m，1 ×3.25 m，4 ×3.50 m和2×4.00 m。全桥共有3个合龙段，分别是2个边跨合龙段和1个中跨合龙段，边跨和中跨合龙段长度均为2 m。

该桥梁是复杂空间曲线、大角度斜交、三向预应力体系的连续梁桥，同时具备该桥型所有施工和计算难点，给施工过程带来巨大挑战。严格保证悬臂施工安全和保证桥梁施工线型成为安全顺利施工的关键。

3.2 悬臂法施工时挠度计算方法

施工过程中挠度计算与计算模型的选取息息相关，而且还有许多不定因素的影响。因此，精确计算挠度非常困难。为了用理论指导施工的进行，必须按施工程序对挠度按弹性挠度和徐变挠度两部分进行计算和控制。各节段立模标高的计算方法如下:

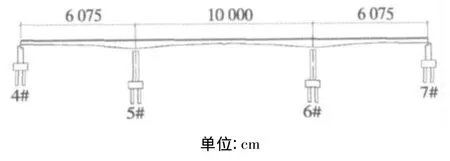
图5 主桥立面布置图Fig.5 The main bridge facade layout

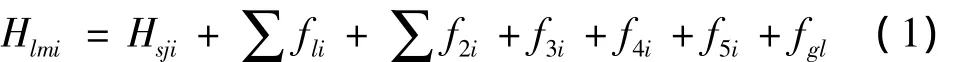
式中:Hlmi为第i节段立模标高;Hsji为第i节段设计标高;∑fli为由各梁段自重在第i节段产生的挠度总和;∑f2i为由张拉各节段预应力在第i节段产生的挠度总和;f3i为混凝土收缩徐变在第i节段产生的挠度;f4i为施工临时荷载在第i节段产生的挠度;f5i为使用荷载在第i节段产生的挠度;fgl为挂蓝变形值。

根据文献［12］，可得得出箱梁梁体任意截面处的挠度表达式为:

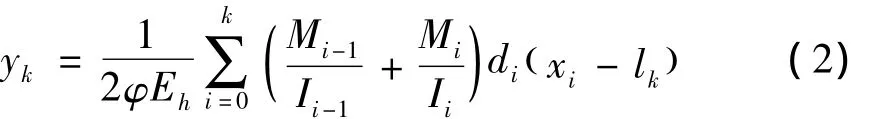
其中:yk为悬臂箱梁k点处的弹性挠度;Eh为混凝土弹性模量;φ为计算所用混凝土刚度折减系数;Mi－1和Mi分别为第i－1点和i点处实梁的截面弯矩;Ii－1和Ii分别为i－1点和i点处的换算截面惯性矩;di为第i梁端的分段长度;xi为第i梁段虚荷载重心至虚梁根部的距离;lk为计算挠度点k至虚梁根部的距离。

徐变挠度可按弹性挠度乘以 [1+φ(t，t0)]求得，φ(t，t0)为徐变系数。

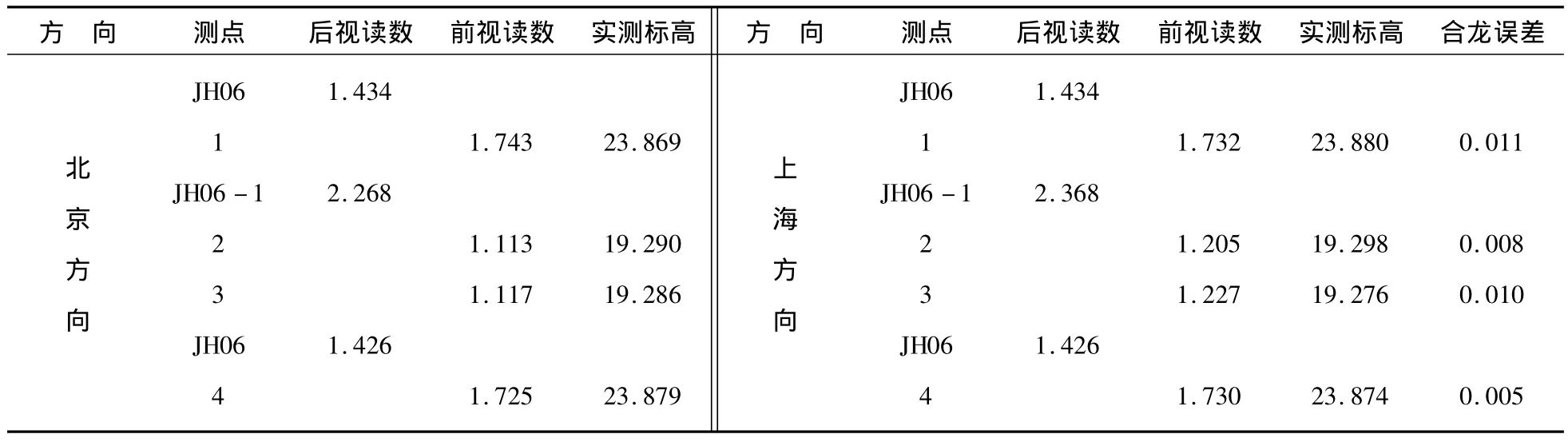
表3 中跨合拢误差Table 3 Closure error of mid－span mm

3.3 计算结果分析

预应力混凝土连续梁悬臂浇筑法施工时，对于其弹性挠度较容易计算。在本部分中，主要对京沪高速跨秦淮新河特大桥的徐变挠度计算进行对比，并得出最终的合理徐变挠度。本文没有单独将徐变挠度单独计算并提取出来，而是以预拱度的形式将各种规范计算结果进行对比。5#墩往北京方向右腹板顶预拱度对比如图6所示 (以5#墩中心为原点，往北京方向梁段长度为坐标横轴负值)。

从图6可以看出，5#墩往北京方向左腹板施工控制数据与上述数据规律大致相同，京沪高速跨秦淮新河特大铁路桥为斜交反对称形式，因此5#墩施工与6#墩施工梁体线性控制数据为反对称形式，只需要提取出5#墩的线性控制数据即可。徐变挠度可由弹性挠度乘以 [1+φ(t，t0)]求得，不同规范计算出的结果差别较大，在成桥过程中，各种变形主要还是以弹性变形为主，因此预拱度也能够体现出在成桥阶段混凝土徐变效应的程度。

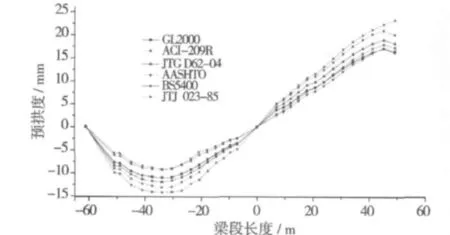
图6 5#墩往北京方向右腹板顶预拱度Fig.6 The pre－camber on the top of right web of 5#pier towards the Beijing direction

在实际施工过程中，线性控制数据还是主要依据04规范计算的结果，从图6可以看出，04规范计算结果与各规范计算结果的平均值较吻合。

3.4 成桥线形控制

桥梁合龙后，在成桥桥面的一个横断面上横向布置2个测点来测量桥面线形。

在施工监控过程中，桥梁跨中处桥面标高与设计标高相差不大，线形控制理想。各节段左右对称位置的标高误差相差很小。成桥后，各节段左右对称位置处的成桥标高相差也较小，在各工况下，箱梁没有出现横向扭转现象。桥梁合龙精度良好，达到设计线形要求。中跨合龙误差见表3。

4 结论

(1)结合我国高速铁路桥梁上部结构主要使用的C50混凝土，具体分析了各主要预测模型的考虑参数，得出主要徐变预测模型的徐变系数变化规律。

(2)经计算分析和参考国内其他学者的试验数据，并对高强混凝土徐变的特点，建议在实际工程中采用GL2000模型、美国混凝土协会ACI－209R模型和我国04规范模型计算徐变系数来考虑徐变效应。

(3)结合京沪高铁跨秦淮新河特大桥实际工程，采用不同的徐变预测模型计算其徐变效应，根据实际情况进行差值分析，为施工过程提供了合理的立模标高，使该桥边跨和中跨合拢误差及成桥线形达到设计要求，为该类型桥梁施工监控提供了参考。

［1］Bazant Z P.Prediction of concrete creep and shrinkage:past，present and future［J］.Nuclear Engineering and Design，2001，203:27 －38.

［2］Gardner N J，Lockman M J.Design provisions for drying shrinkage and creep of normal－ strength concrete［J］.ACI Materials Journal，2001，98(2):159 －167.

［3］ACI Committee 209.Prediction of Creep，Shrinkage and Temperature Effects in Concrete Structures(ACI Committee 209R －92).HIS，1992.

［4］美国各州公路和运输工作者协会.美国公路桥梁设计规范(AASHTO)［M］.北京:人民交通出版社，1997.American Association of State Highway and Transportation Officials.U.S. highway bridge design specifications(AASHTO)［M］.Beijing:China Communications Press，1997.

［5］ BS5400:Pt.1 － 4:1990，Steel，concrete and composite bridges［S］.

［6］JTJ 023—85，公路钢筋混凝土及预应力混凝土桥涵设计［S］.JTJ 023—85，Code for design of highway reinforced concrete and prestressed concrete bridges and culverts［S］.

［7］JTG D62—2004，公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.JTG D62—2004，Code for design of highway reinforced concrete and prestressed concrete bridges and culverts［S］.

［8］项海帆.高等桥梁结构理论［M］.北京:人民交通出版社，2001:4.XIANG Hai-fan.Higher Bridge Structure Theory［M］.Beijing:China Communications Press，2001:4.

［9］楼庄鸿.大跨径梁式桥的主要病害［J］.公路交通科技，2006，23(4):84－87.LOU Zhuang-hong.Main faults in large span beam bridges［J］.Journal of Highway and Transportation Research and Development，2006，23(4):84 －87.

［10］肖 佳，陈 雷，赵金辉.掺合料对C60高性能混凝土力学性能影响［J］.低温建筑科技，2011(4):10－13.XIAO Jia，CHEN Lei，ZHAO Jin-hui.Influence of admixture on mechanical property of C60 high performance concrete［J］.Low Temperature Architecture Technology，2011(4):10－13.

［11］杨小兵.混凝土收缩徐变预测模型研究［D］.武汉:武汉大学，2004.YANG Xiao-bing.Research on prediction model of concrete shrinkage and creep［D］.Wuhan:Wuhan University，2004.

［12］徐光辉.桥梁计算示例集(预应力混凝土刚构桥)［M］.北京:人民交通出版社，1995.XU Guang-hui.Bridge calculate the sample set(prestressed concrete rigid frame bridge)［M］.Beijing:China Communications Press，1995.