罕遇地震作用下HADAS加固某大跨度结构的静力弹塑性分析*

陈代果，姚 勇，邓勇军，杨亚龙，王海军

(西南科技大学土木工程与建筑学院，四川绵阳 621010)

1 工程概况

所研究的体育教学训练中心工程位于四川省绵阳市，以体育教学功能为主，同时可满足举办手球、篮球、排球等项目的地方性、群众性运动会比赛的要求，如图1所示。建筑总高为33.5 m，总长为104.1 m，总宽为 76.2 m，总建筑面积约为 15 940 m2，属于大跨度结构。为了计算分析的需要，根据建筑的使用功能、结构布置，按标高分为6个结构层，其中标高0 ～5.35 m 为第1 层，5.35 ～10.75 m为第2 层，10.75 ～14.75 m 为第3 层，14.75 ～18.6 m 为第4 层，18.6 ～22.59 m 为第5 层，22.59 ～29.99 m为第6层。该建筑物基础采用人工挖孔桩基础，主体结构为全现浇钢筋混凝土框架结构，第1层楼板部分为钢桁架－混凝土板组合结构，屋面为钢网架结构。2007年5月开始修建，2008年3月主体完工，“5.12汶川”大地震发生时，该建筑物正在进行墙面、屋顶施工。由于建筑物仅主体完工，屋顶、墙面大部分未完成，所以地震本身对该建筑物的影响并不严重。而建筑物所在地区抗震设防烈度受“5.12汶川”大地震影响进行了调整，由原来的6度(0.05g)提高 7度(0.10g)，设计特征周期0.40 s，设计地震分组为第二组，建筑场地类别为II类，中硬场地，同时，该建筑物属于大型公共建筑物。

图1 体育教学训练中心Fig.1 Sports teaching training center

在“5.12”汶川大地震中，该体育教学中心遭受到一定的损坏，其损伤主要集中在第2层框架梁、柱部位，破坏状况为梁、柱混凝土保护层脱落，部分梁端、柱端钢筋局部屈服，出现少量塑性铰，如图2所示。为全面了解大震作用下结构的抗震性能和破坏机制，找出结构的薄弱环节，为抗震加固提供参考，拟采用静力弹塑性法对7度罕遇地震作用下，加固前后的结构模型进行分析比较。

图2 体育教学训练中心部分地震损害Fig.2 Seismic damage of sports teaching training center

2 结构有限元模型及阻尼器参数

2.1 结构有限元模型

该结构具有对称性，其1/4平面布置图如图3，截面尺寸见表1，采用大型通用有限元分析软件Midas Gen，结合相关规范及参考文献［1－2］，计算加固所需的阻尼器个数及布置位置，得到加固方案，建立加固前后三维有限元模型如图4所示。

表1 梁、柱截面尺寸Table 1 The section size of the structure model

图3 结构平面布置图Fig.3 Floor plans of structure

基础采用固接，荷载转化为线荷载施加在梁上，梁柱的配筋均按实际配筋情况输入，采用塑性铰模型对结构进行静力弹塑性分析，其中对于梁单元，一般情况是两端内力最大，并且主要承受弯矩荷载，所以在梁两端设置弯矩铰(M)，而柱承受轴力和弯矩的共同作用，故柱两端设置压弯铰(PMM)［3］。

图4 2种有限元结构模型Fig.4 Two kinds of finite element model

2.2 软钢阻尼器参数及力学模型

软钢阻尼器采用上海隆诚实业有限公司研制的开孔式加劲耗能装置(图5(a)，称为制震板(HADAS)［4］。阻尼器相关参数见表2。软钢阻尼器与支撑串联安装在结构中，钢支撑材料为Q235，截面为HW250×250×6×8的H型钢(图5(b)。软钢阻尼器的恢复力模型采用B－Wen模型［5］。

图5 加劲阻尼器Fig.5 The ADAS

表2 软钢阻尼器相关参数Table 2 the related parameters of HADAS

3 模态分析

结构的模态分析是结构地震反应计算和抗震设计的基础，根据结构的模态可以判定结构计算模型的合理性。结构的模态分析包括自振频率和自振振型的分析。自振频率是表示结构刚性的指标，也是判别结构是否会发生共振的依据;而且在使用逐步积分法求解结构动力反应方程时，采用的时间积分步长要根据结构的前几阶自振周期来确定［6］。对于这类体型复杂的大跨度结构，需要考虑高阶阵型的影响，所以模态分析时计算前30阶的振动模态，采用MIDAS/Gen提供的多重Ritz向量法分析结构模态，得到前30阶振型，保证X，Y和Z三向均获得超过90%的振型参与质量。表3给出了加固前后结构前5阶的振型周期，图6所示为前四阶模态振动图。

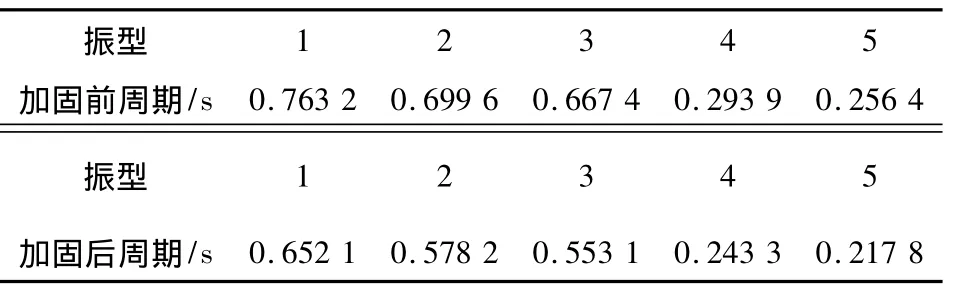
表3 结构前5阶的振型周期Table 3 The first 5 vibration model cycles of structure

从表3及图6可以看出:

(1)该结构前几阶周期分布较均匀，加固前其基本振动周期为0.763 2 s，加固后由于软钢阻尼器增大结构的刚度，导致周期有所降低，基本周期为0.652 1 s，与场地的特征值周期 0.4 s相差较大，不易产生共振;且此类体型复杂的大跨度结构，周期较长，受特征周期长的场地影响大。

(2)加固前后的结构前四阶振动模态相同(如图6)，第一阶振型均为沿结构水平轴Y向水平振动，第二阶振型主要沿结构水平轴X向水平振动，第三振型为绕Z向竖向对称扭转为主，其高阶振型主要为竖向的对称和反对称振动为主。

(3)结构前面的振型均为整体振动，中部的大空间由于设计的刚度较大，发生局部竖向振动的几率较小，表现为高阶振型，振型参与系数较小，对结构影响不大。

(4)结构的前四阶振型为水平方向振动，而且其频率低于以竖向为主的第五阶至其他高阶振型。分析认为这是由于结构水平约束的刚度相对于竖向约束刚度要小，从而引起结构整体水平振动的结果，另一方面说明结构的水平振动在此结构动力反应中起着重要作用。

图6 加固前(后)结构前4阶模态振动图Fig.6 The first 4 mode vibration figure of structure

4 静力弹塑性分析

静力弹塑性分析法(Push－Over)是通过施加水平单调递增荷载来进行分析的一种非线性静力分析方法，它研究结构在地震激励下进入塑性状态时的非线性性能。采用对结构施加呈一定分布的单调递增的水平力的加载方式，用二维或伪三维数学模型代替原结构，按预先确定的水平荷载加载方式将结构“推”至一个给定的目标位移，来分析其进入非线性状态的反应。从而判断结构及构件的变形受力是否满足设计及使用功能的要求，选定的加载方式要能代表结构在地震中相应的水平惯性力。当结构为低矮建筑时，地震作用以第一阵型为主，此时用线性的倒三角分布方式加载即可代表真实的地震作用。随着房屋高度的增加，高阶振型对结构地震效应的影响就不能忽略，因此，长周期结构宜采用非线性的水平力加载［7］。

4.1 分析条件

根据前面的模态分析结果，该大跨度结构加固前后周期较小，第一阶振型起主要作用，采用倒三角荷载分布进行分析精度可以满足要求，故选择倒三角加载形式对加固前及加固后2种结构进行push－Over分析。在定义Push－Over工况时，除了考虑上述水平荷载外，应首先定义重力荷载作用作为Push－Over第一工况，这里重力荷载为1.0自重+1.0恒载+0.5活载，水平力与其组合作为第二工况。计算时，首先计算第一工况下的内力和变形。第二工况下的计算是在第一工况下内力和变形的基础上施加水平荷载，水平荷载不断增加，结构侧移不断增大，直至到达规定的位移为止。该结构中选取结构顶点位置的节点作为整体结构的水平侧移或控制位移。

采用能力谱法确定其在7度罕遇地震作用下的性能点，评价结构在大震作用下是否满足抗连续倒塌的要求，考察采用软钢阻尼器加固后结构的抗震性能，分析中荷载分布取第一阶模态，考虑初始荷载影响，阻尼比为5%。图7所示为结构理想的能力曲线［8］。

图7 结构理想的能力曲线Fig.7 The ideal capacity curve of structure

4.2 结果分析

4.2.1 层间剪力－位移分析

图8所示为加固前与加固后模型在倒三角分布作用下各楼层处的层间推覆曲线。其横坐标为层间位移，纵坐标为层间剪力。

图8 2种模型的能力曲线Fig.8 The capacity curve of two modes

从图8可以看出:随着楼层逐层增高，推覆曲线变得越来越陡，加固前与加固后的推覆曲线趋势大致相同，与图7所示结构的整体推覆曲线相比，2种模型第1层的位移均增加直至屈服，加固前的2层位移也可到达屈服平台，而加固后的2层停留在小震不坏之前，基本处于弹性工作范围内;到第3，4，5和6层以后，2种模型的位移都很小，结构未进入塑性屈服状态，加固后的曲线更短一些，且从加固前后各层的位移来看，可以发现在相同的水平荷载作用下，加固后结构的屈服位移和极限位移值较小，说明采用软钢阻尼器加固后，在相同的推覆荷载下，抵抗变形的能力增大，整体抗震性能提高。

4.2.2 性能点评价

图9 2种模型的性能点曲线Fig.9 The performance point curve of two modes

使用ATC－40［9］中建议的等效阻尼法，评估塑性需求谱并和能力谱相比较，从而得到性能控制点。该规范提供2种计算方法:(1)首先评估处于塑性状态下结构的等效阻尼，并且产生相应的需求谱，性能控制点通过反复计算得到;(2)通过假定了延性需求曲线并且使用相应的等效周期和等效阻尼比，来评估性能控制点和得到与能力谱相交的方法。2种方法基本原理相同，其中与等效粘滞阻尼比有关的为弹性地震需求谱，而与结构位移延性系数有关的为弹塑性地震需求谱，这里选用第2种方法来评价结构在大震作用下的反应。图9所示为各模型的能力－需求谱曲线。

从图9可以看出:2种模型均能满足7度罕遇地震抗倒塌验算(即结构的能力曲线在大震失稳控制点之前穿过需求谱曲线)，但是，加固前结构的能力谱曲线相对于加固后的结构，其整体结构的延性较差，体现在能力谱曲线的平台部分短，说明原结构的抗倒塌能力弱，而加固后由于加入了软钢阻尼器，其良好的耗能能力使结构的抗倒塌能力得到有效提高。

表4 2种模型延性比和位移Table 4 The ductility ratio and displacement of two modes

对比分析加固前后的位移可以发现，原结构和加固后结构的屈服位移及极限位移比较小，均小于7度罕遇地震下的目标位移(1/50);加固后结构的延性比(表4)更大，说明软钢阻尼器的存在增加了结构的耗能能力，进一步提高其抗震性能。

4.2.3 塑性铰发展

采用的塑性铰为FEMA－356［10］铰，对每一个自由度，都定义1个用来给出屈服值和屈服后塑性变形的力－位移曲线，通过A－B－C－D－E的曲线来控制，如图10所示，其中点B代表铰的屈服，A－B之间假定结构为刚性。当铰达到C点时，开始失去承载能力，点IO，LS和CP代表铰的能力水平，它们分别对应于直接使用、生命安全及防止倒塌［11］。

图10 力－位移曲线(弯矩－转角曲线)Fig.10 The force－displacement curve

结合该结构在“5.12”地震中的主要破坏部位及结构分析所得到的相对薄弱位置情况，其2层为刚度突变的主要部位，容易发生局部破坏，故考察加固前后该部位在推覆分析中塑性铰发展的情况，分析软钢阻尼器对塑性铰发展的影响。

通过分析图11可知:当水平推覆位移为40 mm时，2种模型大部分构件处于弹性阶段，原结构仅在中部环形区域的两端有少部分梁进入IO阶段，而加固后中该部位梁均介于B－IO阶段，说明加入阻尼器后，结构的抗推覆能力加强;当加载到70 mm时，原结构已有部分构件进入了LS－CP阶段，影响结构的正常使用，加固后仅有少部分达到LS阶段;继续加载至100 mm时，原结构出现大量的红色区域，证明构件超过C点，产生塑性铰，且主要集中在杆件交汇部位，也是该结构的刚度突变处，在地震作用下易发生破坏，不利于抗震，对于阻尼器加固后，结构虽然也有少量塑性铰产生，但由于阻尼器的作用，使结构的刚度重分布，塑性铰位置转移到结构的周边处，远离主要承重构件，提高了结构的抗倒塌性。

图11 2种模型第2层梁塑性铰发展图Fig.11 The plastic hinge development figure of the second layer’s beam of two modes

5 结论

(1)加固前后模型均能满足7度罕遇地震抗倒塌验算，但是原结构二层位置较薄弱，容易发生局部破坏。加固后结构刚度更为均匀，大震下的抗倒塌能力增强。

(2)阻尼器使结构的刚度重分布，塑性铰位置转移到结构的周边处，远离主要承重构件，大大提高了结构的抗倒塌性。

(3)结构的薄弱环节出现在第2层，塑性铰分布图表明大量的塑性铰均密集出现在该部分的梁、柱构件上，这与地震对结构的实际破坏情况是吻合的。加固前后结构均具有一定的强度与变形能力储备，可以满足“大震不倒”的要求，软钢阻尼器对结构塑性铰的分布及出铰顺序有较大影响。

［1］周 云.耗能减震加固技术与设计方法［M］.北京:科学出版社，2006.ZHOU Yun.Reinforcement design for earthquake resistant of energy dissipation structure［M］.Beijing:Beijing Science Press，2006.

［2］GB 50011—2001，建筑抗震设计规范［S］.GB 50011—2001，Code in seismic design of buildings［S］.

［3］Anil K C，Rakesh K G.A modal pushover analysis procedure to estimate seismic demands for buildings:Theory and Preliminary Evaluation［R］.PEER Report，2001(03).Pacific Earthquake Engineering Research Center，College of Engineering University of California Berkeley，2001.

［4］Skinnner R I，Kelly I M，Heine A J，et al.Hysteresis dampers for the protection for the protection of structures from Earthquake［J］.Bull N.Z，Nat Soc for Earthquake Engineering，1980，13(1):22－26.

［5］Tyler R G.Tapered steel energy dissipaters for earthquake resistant structures［J］.Bulletin of New Zealand National Society for Earthquake Engineering，1978，11(4):282 －294.

［6］李 斌.高层建筑结构模态分析方法的应用［D］.上海:同济大学，2006.LI Bin.Application study on structural modal analysis method for high－rise buildings［D］.Shanghai:Tongji U-niversity，2006.

［7］叶燎原，潘 文.结构静力弹塑性分析原理和计算实例［J］.建筑结构学报，2000，21(1):37 －42.YE Liao-yuan，PAN Wen.Structure Pushover analysis principles and an example［J］.Journal of Building Structures，2000，21(1):37 －42.

［8］汪大绥，贺军利，张凤新.静力弹塑性分析(Pushover A-nalysis)的基本原理和计算实例［J］.世界地震工程，2004，20(1):45 －53.WANG Da-sui，HE Jun-li，ZHANG Feng-xin.The basic principles and an example of the nonlinear static analysis(on Pushover Analysis)［J］.World Earthquake Engineering，2004，20(1):45 －53.

［9］ATC40，Seismic evaluation and retrofit of concrect Buildings［S］.

［10］Prestandand and commentary for the Seismic Rehabilitation of Buildings［S］.Federal Emergency Management Agency.FEMA 356/November，2000.

［11］北京金土木软件技术有限公司.Sap2000中文版使用指南［M］.北京:中国建筑工业出版社，2009.Beijing Golden civil Software Technologies Ltd.The Sap2000 of Chinese edition guide［M］.Beijing:China Building Industry Press，2009.