改进的CORDIC限幅器
2012-09-20李雪萍刘昌银蔡超时杨刚
李雪萍,刘昌银,蔡超时,杨刚
(中国传媒大学信息工程学院,北京100024)
1 引言
自 1959 年 Volder J[1]提出坐标旋转数(Coordinate Rotation Digital Computer,简称 CORDIC)以来,CORDIC算法得到了广泛的应用[2]。CORDIC的优越性表现在它通过简单的移位加减操作就能完成三角函数,指数,对数,乘法和除法,开方等运算。并且CORDIC是一种规则化算法,结构简单,便于硬件实现。因此,它普遍应用于信号处理,通信系统等领域。
限幅运算是畸变类峰均比抑制算法极其重要的组成模块之一[3-4]。限幅是将高峰值的信号截断,而其后的滤波引起一定程度的峰值再生,为获得良好的抑制效果,需要多次迭代。因此,每次迭代每个模块需合理的支配硬件资源,尤其是DSP资源。传统限幅操作通过乘除运算实现。FPGA虽内嵌了专用的DSP模块,但峰均比抑制算法中FFT和FIR模块包含了大量的乘法运算,其他模块可支配的DSP较少。同时传统限幅器的除法模块由较大的组合时序逻辑实现,限制了设计的时钟速率。因此,提出新的限幅算法,减小硬件开销,提高设计速率有着重要意义。
Altera公司早在2007年提出了一种极坐标限幅(Polar Clipping,PC)(以下简称 PC 限幅器)[5-7],PC限幅器是一种基于CORDIC旋转的限幅器。它将传统限幅器的乘除运算转化为寄存器移位加减运算,极大地减少了硬件资源的使用,同时避免使用除法极大地提高了时钟速度。PC限幅器采用了两个独立的CORDIC模块分别完成幅值计算和限幅向量的旋转,模块间通过存储的相位旋转变量通信。PC限幅器需额外存储旋转相位信息,增加了设计的复杂度。
文章提出了一种改进的CORDIC限幅器(Improved CORDIC Clipper)(以下简称IC限幅器)。IC限幅器将幅值计算和限幅向量的旋转合并到同一个CORDIC模块中,将模块间的通信转化为模块内的通信,从而避免存储额外的相位旋转变量,简化了设计。仿真表明,相比于传统限幅器,IC限幅器使用的资源减少了近一半,最大时钟速率提高了约2.4倍。
文章第二部分介绍了CORDIC算法的原理,第三部分阐述了传统限幅器的设计,第四部分是关于PC限幅器原理,第五部分讨论了IC限幅器的设计原理及考虑,最后两部分分别分析了仿真结果以及给出了设计的结论。
2 CORDIC算法
CORDIC有旋转法和矢量法两种,本文只讨论旋转法。
假设点A沿逆时针方向旋转θ角度至点B,点A 坐标为(xi,yi),点 B 为(xi+1,yi+1),见图 1。经推导有如下关系:

同样旋转θ角,当点A沿顺时针方向转至点B'时,有

设每次旋转的角度为α=arctan2-(i-2),

其中

zi是当前坐标点与目标点相差的角度,决定了当前旋转方向。则总的旋转度数为

旋转次数n决定了算法精度,经过n次旋转,向量的幅度因子
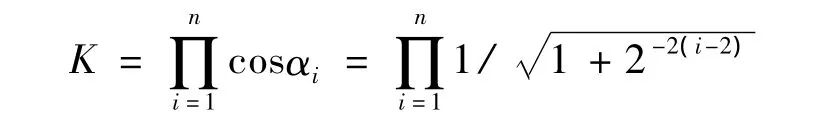
当n足够大时,K≈0.607253。

图1 坐标旋转示意图
3 传统限幅器
3.1 CORDIC求幅值
由(3),设原始向量(x0,y0),其向量角 θ,使用CORDIC旋转模式,经过n次旋转,旋转角度为-θ,则

变量xn与该向量幅值息息相关。
CORDIC算法的关键之一是旋转方向的确定。(3)中zi决定了旋转方向,由于每次旋转的角度已知,可以将各次旋转角度事先存储在ROM表中。求幅值的CORDIC算法特殊性在于它是将向量旋转到x轴上,因此,旋转的方向可由y向量确定。

CORDIC旋转角θ的大小和迭代次数n相关,其取值范围为[-99.88o,99.88o],而不是整个象限[-180o,180o],因此,第二、三象限不在旋转范围内。迭代前应将初始向量变换到一、四象限[8]。
CORDIC算法引入了幅度增益因子K,初始向量(x0,y0)经CORDIC旋转的输出并不是其幅度,而是幅度的1/K。
3.2 传统限幅器设计
限幅器是畸变类峰均比抑制算法中的重要模块之一。通过限幅器,大功率的信号被抑制,降低了OFDM峰值功率,从而降低了OFDM的峰均比。
限幅是将超过设定门限的信号截断,是一种非线性操作。输入复信号c(n),设定限幅门限为A,限幅原理如下:

其中|c(n)|表示复信号c(n)的模。当c(n)幅值小于等于门限值A时,限幅器没有非线性操作,当c(n)幅值大于A时,限幅器将c(n)的幅值限定在A。
传统限幅器由乘除运算实现,见图2。MAG模块计算复信号幅值,MULT模块实现如下功能:若幅值大于门限值,输出 VCLIP与向量的乘积,否则MAG与向量乘积。DIV模块完成除法运算。其中乘法用FPGA自带的专用乘法器实现,以提高乘法运算速度。除法可直接调用Altera的IP核,速度较慢。
如上所述,MAG模块输出幅值MAG并不是输入的幅度,而是幅度的1/K。
4 PC限幅器
Altera公司的PC限幅器是一种完全基于CORDIC算法的限幅器。CORDIC首先变换笛卡尔坐标为极坐标,选择器选择输出幅值R或门限值Amax,第二个CORDIC模块与第一个相反,它将极坐标重新转化为笛卡尔坐标。
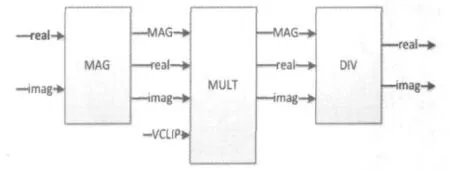
图2 传统限幅器
PC限幅器用CORDIC算法的移位加减运算替代了乘除运算。不仅减少了资源消耗,也提高了运算速度。它采用了两个CORDIC模块分别完成幅值计算和限幅向量的旋转,模块间通过存储的相位旋转变量通信。

图3 PC限幅器
5 改进的CORDIC限幅器
PC限幅器CORDIC模块2将极坐标沿着CORDIC1的旋转路径旋转回笛卡尔坐标。这意味着需要存储CORDIC1旋转方向,增加了设计的复杂度。在设计CORDIC算法的限幅器时,可充分考虑逻辑和资源复用以简化程序设计和减少资源消耗。IC限幅器在PC限幅器的基础上做了改进。
传统限幅器使用了CORDIC算法计算信号幅值。它通过将向量旋转到x轴,以此计算复信号幅值,向量的分量决定了旋转方向。IC限幅器在同一CORDIC模块中经过相反的旋转,将限幅向量由x轴旋转到与信号重合位置,以实现限幅操作,算法流程如图4。
输入 vinit是预设的限幅门限。c1x0,c1y0是CORDIC1的初始寄存器值,c2x0,c2y0是 CORDIC2的初始寄存器值,c1yi是CORDIC1每次迭代的y向量。
输入信号有效时,首先判断其是否在一、四象限,若在,CORDIC1初始值即为输入向量值,CORDIC2为(vinit,0),否则 CORDIC1 为其原点对称值,CORDIC2为(-vinit,0)。迭代中,若当前 CORDIC1的 y值 大 于 0,则 CORDIC1,CORDIC2分别顺时针、逆时针旋转,否则相反。迭代结束后,若幅值MAG大于门限Vclip,选择器选择输出CORDIC2旋转输出值,否则输出原输入向量。

图4 改进的CORDIC限幅器
由第2部分得知,CORDIC输出与输入幅值存在比例关系K,在设定初始值时考虑到这点,可避免在输出端作乘法以补偿K因子。设仿真得到限幅门限值为,则vinit应设为max*K,由此旋转后的I分量和Q分量与原信号的I、Q分量具有可比较性,而不用额外作比例转换。Vclip应设为max/K,如此这样,CORDIC1输出幅值与限幅门限可直接比较,进一步简化了设计复杂度。
6 仿真结果
6.1 仿真系统搭建
仿真系统如图5所示。仿真激励是一个时隙的CMMB信号[9],每个时隙由53个 OFDM 帧组成,每个OFDM帧有3076个有效子载波和1020个零载波。有效子载波采用QPSK映射方式。
激励信号首先经过4倍升采样滤波。用数字信号表示模拟信号波形时,升采样可以更真实地反映模拟信号的峰均比分布情况。研究表明,4倍升采样已足够表示真实信号的时域分布[10]。
升采样后的CMMB信号进入限幅器,高电平信号被截断。限幅引入了非线性误差,带内表现为星座图弥散和旋转,带外表现为噪声迭起。其后的滤波模块可有效地降低带外噪声。

图5 仿真系统框图
6.2 仿真效果
激励信号经过4倍上采样和限幅滤波后,原始信号幅值分布更加平滑,原来出现概率较低的大信号消失,峰均比有效降低,如图6。

图6限幅前后时域分布
6.3 精度
CORDIC算法的迭代次数决定了运算复杂度和精度,有限的迭代次数导致了有限的精度。Matlab浮点运算可以得到精度很高的结果,以此为基础,可以分析理想限幅器和传统限幅器间的误差大小。
输入4096*53个随机数据,经图5所示数据处理,定义变量SNR来衡量IC限幅器的精度,信噪比

其中,Pclip是理想限幅器输出总功率,Perr是总误差功率。SNR(dB)随迭代次数N变化如表1:

表1
由表可以看出,随着迭代次数的增加,SNR越来越高,IC限幅器的精度越来越高。迭代8次SNR为53.52dB,满足一般应用。
6.4 资源使用和时钟速率
基于Altera的EP3C25F256C8平台,输入输出16比特。传统限幅器模块乘法输出结果截取19比特,CORDIC算法迭代8次,IC限幅器,PC限幅器及传统限幅器资源使用情况如表2:

表2
可以看出,IC限幅器相比于传统限幅器和PC限幅器,减少了资源消耗。传统限幅器设计组合逻辑和时序逻辑比例约为2.8,其中的除法模块达到了460∶82≈5.6,庞大的组合逻辑,对时序提出了挑战。当除法器的分子输入为19比特时,仿真结果表明,IC限幅器fmax可达220.4Mhz,而传统限幅器只有92.58Mhz。随着除法输入比特数的增加,组合逻辑的比例随之增加,时钟速率不断下降。
使用了大量组合逻辑的除法模块,不适合应用于高速设计。基于IC算法的限幅器,采用了简单的移位运算替代传统的乘除运算,同时将PC限幅器模块间通信转化为模块内通信,不仅减少了资源的使用,也极大地提高了时钟速率。
7 结论
IC限幅器采用简单的移位加减运算替代传统限幅器的乘除运算,它抑制了OFDM大信号出现的概率,有效地降低了其峰均比。当除法模块分子输入19比特,CORDIC迭代8次时,相比于传统限幅器,IC限幅器逻辑资源使用减少了近一半,DSP使用0个,并且最大时钟速率提高了约2.4倍。
CORDIC迭代次数限制了其精度。迭代8次时,SNR为55.52dB,满足一般用途。
[1]JACK E VOLDER.The cordic trigonometric computing technique[J].Electronic Computers,IRE Transaction on,1959.9,EC-8(3):330-334.
[2]Meher P K,Valls J,Tso-Bing Juang,Sridharan K Maharatna K.50 Years of CORDIC:Algorithms,Architectures and Applications[J].IEEE Transactions on,2009,56(9):1893-1907.
[3]Xueping Li,Peng Zhang,Lanxiang Jiang.HPA linearization technique of cascading PAPR reduction and predistortion[J].Image and Signal Processing,2011,(10):2818-2821.
[4]吴炳洋,程时昕.多载波通信中峰均比问题研究[D].南京:东南大学,2004.
[5]Altera Corporation.Crest Factor Reduction for OFDMA Systems[EB/OL].Altera官方网站http://www.altera.com.cn/literature/an/an396.pdf.2007.
[6]Altera Corporation.Crest Factor Reduction[EB/OL].Altera官方网站:http://www.altera.com.cn/literature/an/an396.pdf.2007.
[7]Altera Corporation.Altera wireless solution[EB/OL].Altera官方网站 http://www.altera.com.cn/literature/an/an396.pdf.2008.
[8]Xiao Hu,R G Harber,Steven C Bass.Expanding the Range of Convergence of the CORDIC Algorithm[J].Ieee transacation on computers,1991,40(1):13-21.
[9]GY/T 220.1-2006.移动多媒体广播 第1部分:广播信道帧结构、信道编码和调制[S].北京:国家广播电影电视总局,2006.
[10]江涛,朱光喜.OFDM无限通信系统中峰均功率比的研究[D].武汉:华中科技大学,2004.
