抗滑桩结构土拱的分拆与联合研究

林治平，刘祚秋，商秋婷

（中山大学 应用力学与工程系，广州 510006）

1 前 言

土拱效应是土压力从屈服区域转移到临近静止区域的现象[1]。抗滑桩间普遍存在土拱效应，根据拱脚受力性质及位置不同，土拱可分为摩擦拱和端承拱[2]，统称为单独拱。但实际工程中，单独拱并不孤立存在，而以两者联合的形式共存，其合体称为联合拱[3]。3种拱的区域构成如图1所示。

有关土拱效应的研究可谓方兴未艾，目前研究内容主要集中在土拱的形成发育[4]、拱强度影响因素及规律[5]、拱体几何特征和合理桩间距[6]等方面，并得出大量有益的结论。然而绝大部分结论皆基于联合拱模型得出，尤其在数值模拟和模型试验方面，暂未见有关单独拱模型的专门研究，以致无法认清单独拱间差异性及联合机制，最终影响到联合拱的研究。笔者认为，这是对土拱效应认识难以深化和细化的瓶颈所在。

基于此，本文从数值模拟角度出发，采用FLAC3D软件分别建立了摩擦拱、端承拱和联合拱3种模型，遵循“先分拆，后联合”的主线，探讨了3种拱在前述研究内容中的具体规律，提出了研究土拱效应的新思路，以期为同类研究提供参考。

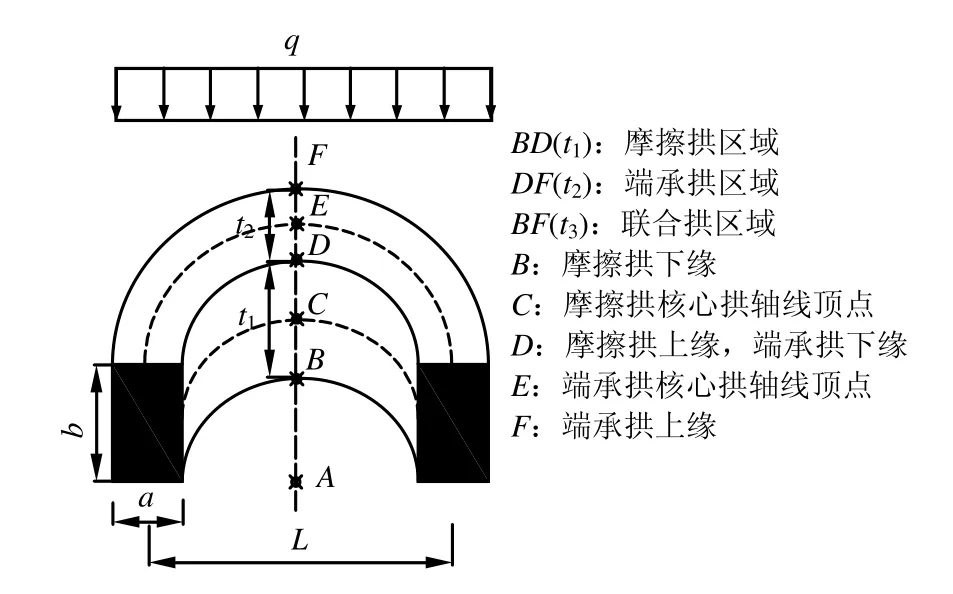
图1 3种土拱的区域分布Fig.1 Distributions of three soil arches

2 模型建立

联合拱模型已有较多文献建立，如图2左半部分所示。方桩截面长、高分别为a、b，桩中心间距为L。采用平面应变模型，沿深度方向取单位厚度。根据对称性，沿x向取相邻两桩中心间距范围。为减弱边界效应影响，沿 y向桩前后土体范围均取10b[7]（特别地，端承拱模型取10a）。

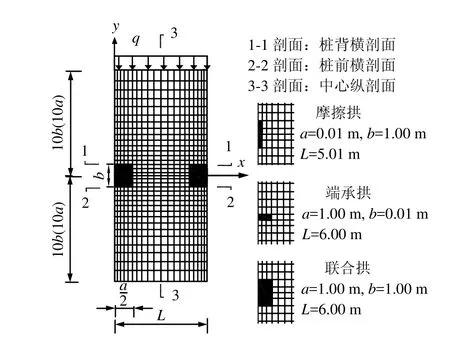
图2 3种拱的基本数值模型及差异性处理Fig.2 Basic numerical model and different treatments of three arches

两单独拱模型的建立与联合拱基本一致，其差异处仅在于对桩截面尺寸的选取不同。为实现“单独”，单拱建模时，可通过移除另一相对单拱的拱脚来消除后者的影响。摩擦拱和端承拱的拱脚分别存在于桩侧和桩背处[8]，故只须分别令a、b取很小值即可。经多方案试算，当桩截面短、长边之比（摩擦拱为a/b，端承拱为b/a）不大于0.01时，则弱拱相对于强拱几乎可忽略，近似认为满足“单独”要求。3种拱模型的差异性处理如图2右半部分所示。

土体和桩体网格分别采用摩尔-库仑模型和弹性模型，桩-土间建立无厚度的三角形接触单元。除加载边界外，其余边界均设置法向位移约束，桩在水平方向上全约束[7]。滑坡推力可通过在模型后侧边界施加均布力q来模拟，除特别说明外，q均取20 kPa（文中应力以压为正）。

采用的材料参数如表1所示。接触面的法向和切向刚度参照文献[9]选取，接触的粗糙程度用接触系数Rinter表示，则接触面的摩擦角和黏聚力可按桩周土体相应参数值乘Rinter确定[7]，本例取Rinter=0.5。

表1 材料性质参数Table 1 Property parameters of materials

3 土拱形成和发育

3.1 形成历程

Rchard曾描绘出土拱为近似悬链线的主应力流线[10]，这意味着透过主应力偏转可反映土拱的形成过程，且偏转范围可确定土拱的分布。

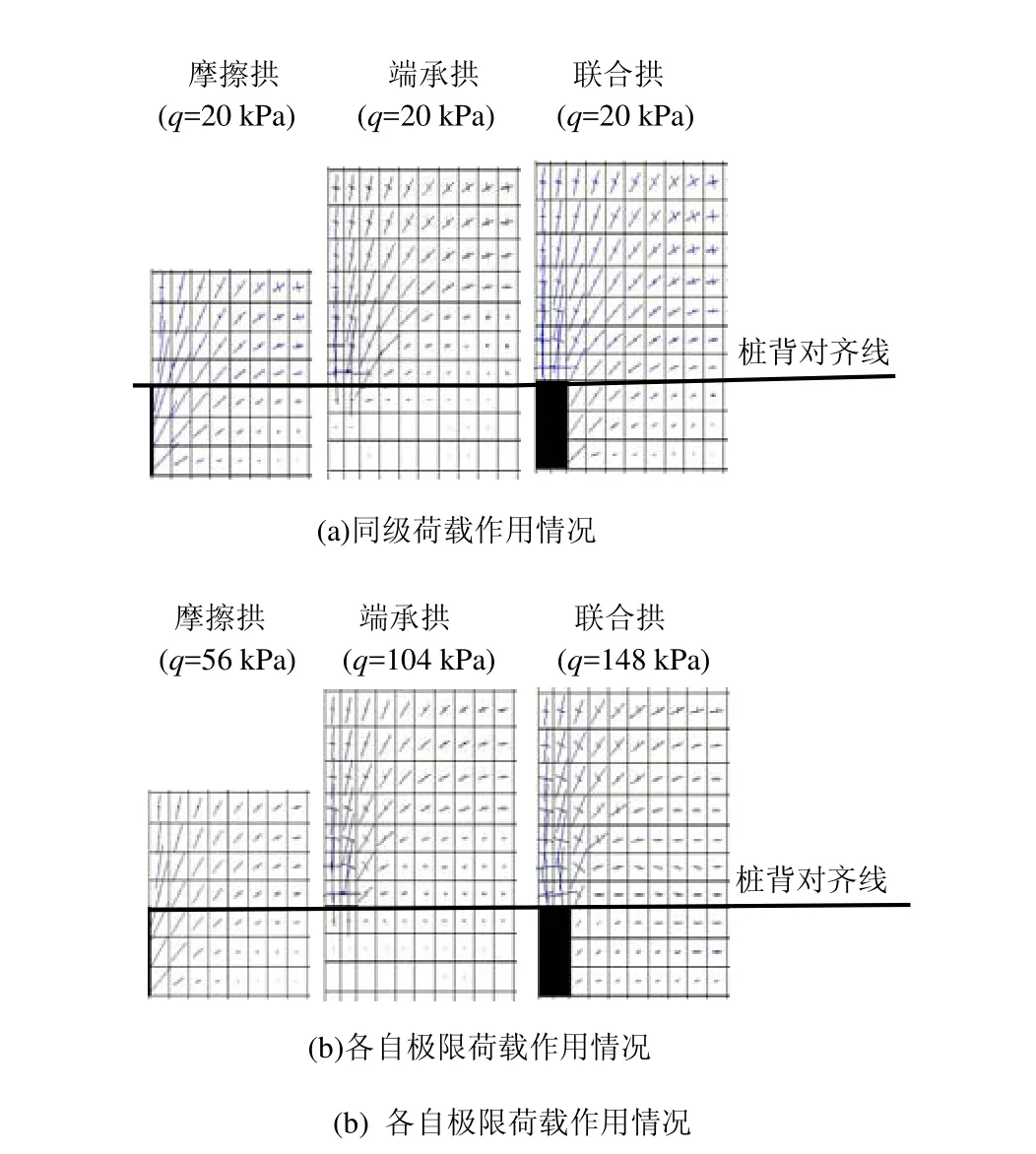
图3 3种拱模型的主应力偏转Fig.3 Principal stress’s deflection of three arches

3种模型取同级荷载和各自极限荷载(后文得出)分别进行模拟，截取主应力偏转较明显的网格部分(据对称性取模型左半部分)如图 3所示。由偏转程度可知，3种拱的主应力偏转次序皆由两侧到中间,由近桩到远桩，但正对桩背处偏转不明显。就偏转范围而言，摩擦拱主要集中在桩间及桩间后邻域内，而端承拱则分布在桩背及离桩后一定距离处，沿桩后延伸范围较摩擦拱大。联合拱的主应力偏转率先从桩侧和桩间处开始，逐渐向桩后发展，偏转范围近似为两单拱的叠加。因此，在联合拱中，摩擦拱先形成，端承拱后形成，期间两单拱共同发展。

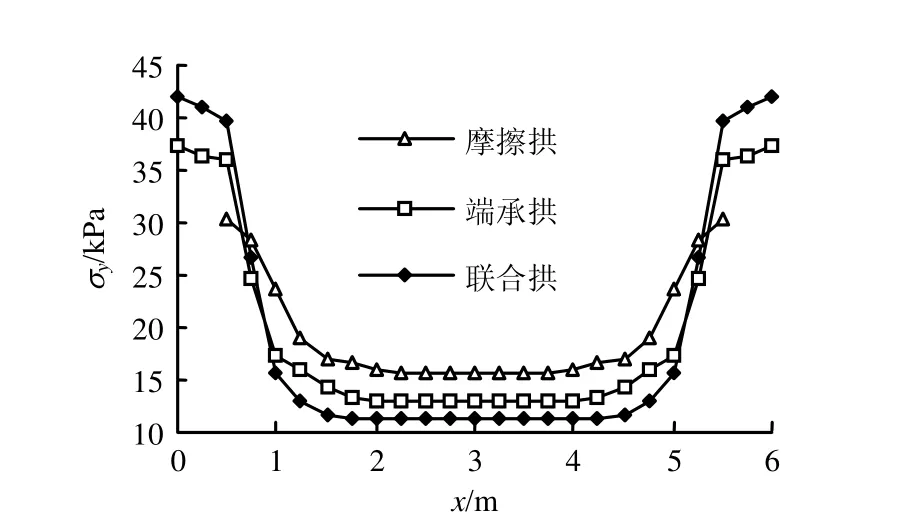
图4 桩背横剖面处σ y分布Fig.4 Distributions of σ y of cross-section in the back of piles

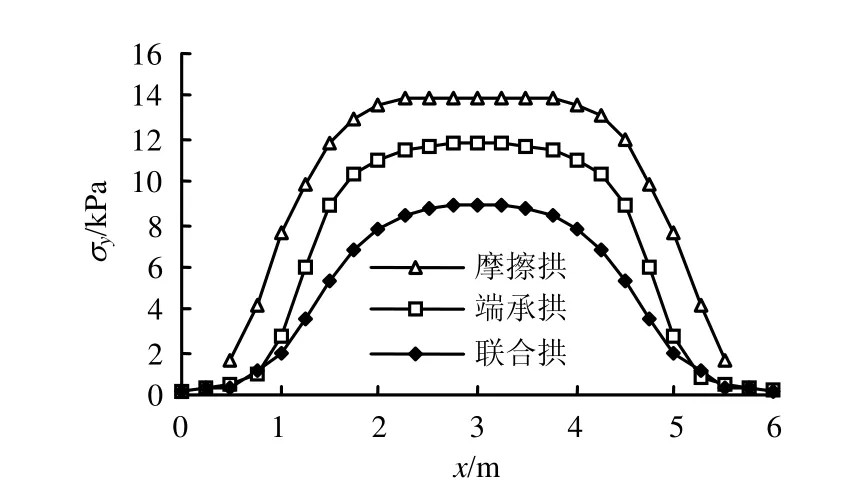
图5 桩前横剖面处σ y分布Fig.5 Distributions of σ y of cross-section in the front of piles

另由图4和图5可知，桩背横剖面处σy由中间向两侧逐渐增大，桩前横剖面处情况则恰好相反，且均值皆明显减小。这表明随着土拱形成，较多的推力荷载由土体逐渐卸至两侧桩体，且易知同级荷载下，3种拱卸荷程度为:联合拱>端承拱>摩擦拱。

3.2 几何分布

均布荷载下土拱的合理拱轴线为抛物线，且拱体沿拱轴向等厚[2]，故只需确定图1中各控制点的y坐标即可完全确定3种拱的几何分布，这可通过分析3种模型中心纵剖面处的应力变化规律获得。

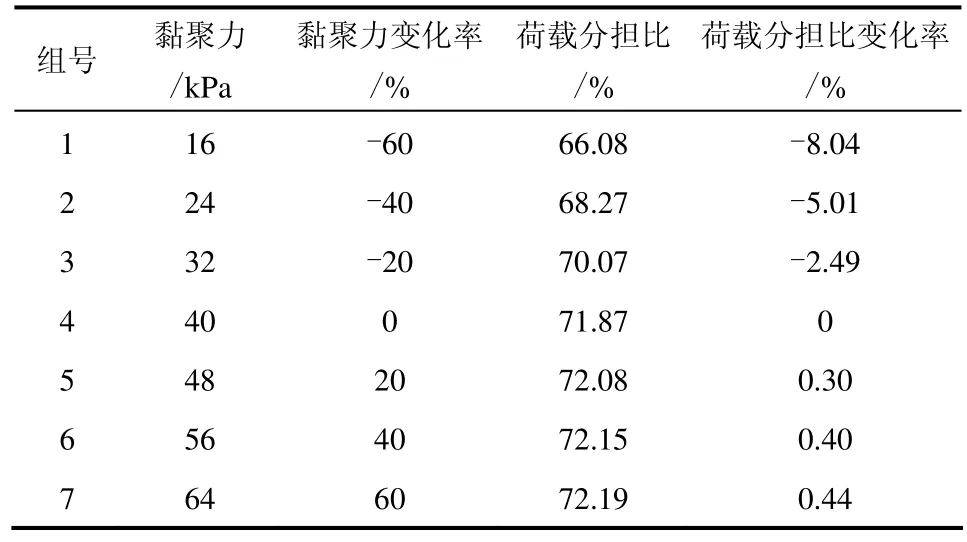
由图6可知，自桩后远处逐渐靠近桩时，3种模型中心纵剖面处σy逐渐减小，且递减速度与 y坐标相关。在y =5～1.75 m区段，端承拱和联合拱的σy递减较快且几乎同步，而摩擦拱对应的曲线则较平缓，与前两者曲线偏离程度渐大。自y =1.75 m处起，端承拱曲线开始变缓，与联合拱曲线逐渐分离，而摩擦拱曲线则加速递减，与联合拱曲线近乎平行。至y =-0.5 m处，3种拱的σy递减基本停止。这就说明，在y =1.75 m以后的区段，端承拱起主导作用，摩擦拱十分微弱，而在y =1.75 m以前区段，则摩擦拱起主导作用，于是由此可确定，yB=－0.5 m、yD= 1.75 m、yF=5 m。

同理分析图7可知，3种模型中心纵剖面处σx先逐渐增大，各至不同y处到达峰值，随后开始减小，峰值点位置便是核心拱轴线顶点位置[11]。对于端承拱和联合拱模型，峰值点皆约处于y =2.5 m处，摩擦拱情况则约处于y =1.25 m处，于是可确定yC=1.25 m、yE=2.5 m。

综上可进一步算得两单拱的拱厚分别为：t1=yD-yB=2.25 m，t2=yF-yD=3.25 m。联合拱拱厚t3=t1+t2=5.50 m。联合拱厚度中，端承拱在其中占较大比例。

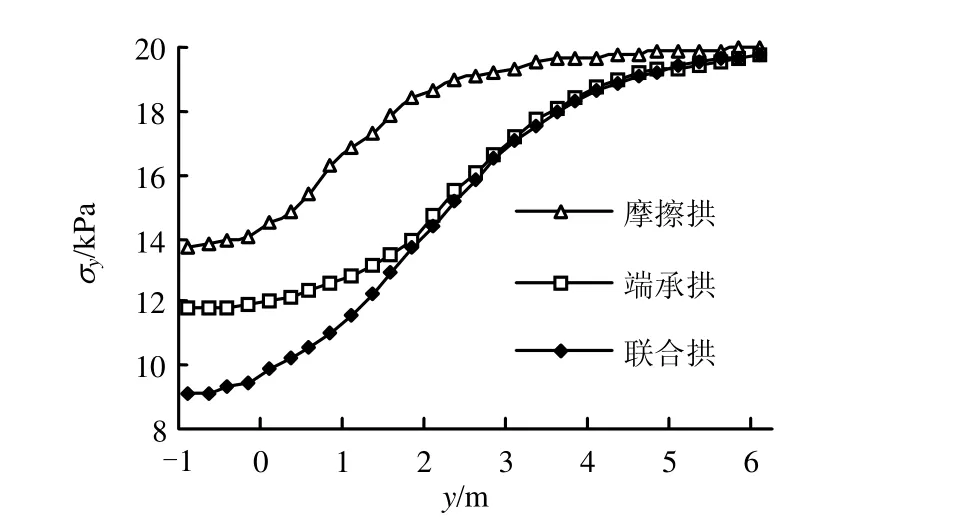
图6 桩间中心纵剖面处σ y分布Fig.6 Distributions of σ y of the middle section between piles

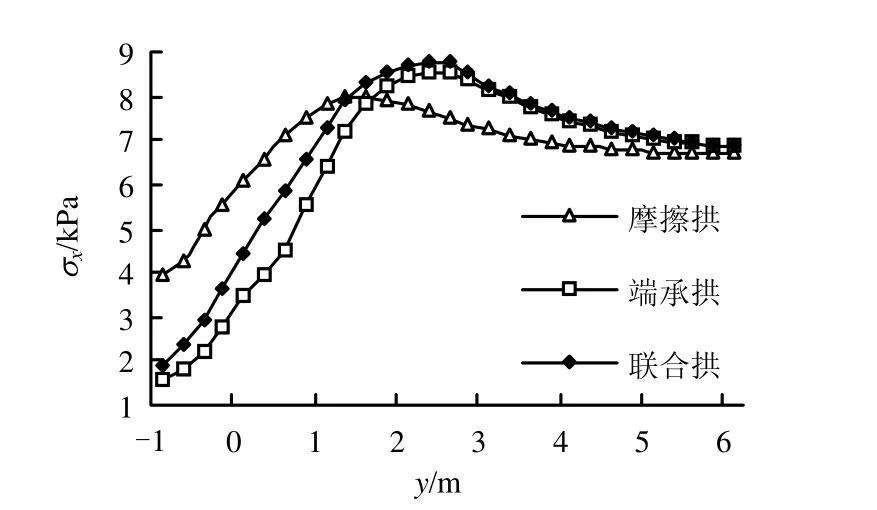
图7 桩间中心纵剖面处σ x分布Fig.7 Distributions of σ x of the middle section between piles

3.3 极限状态

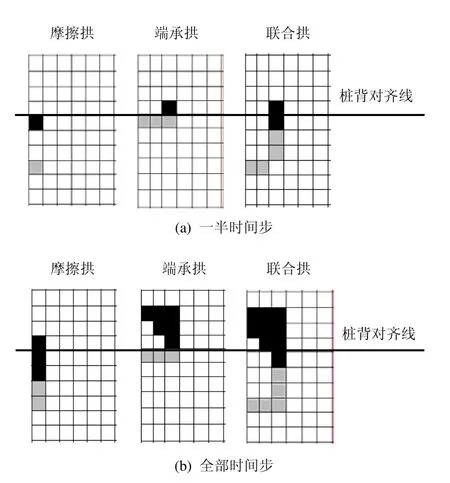
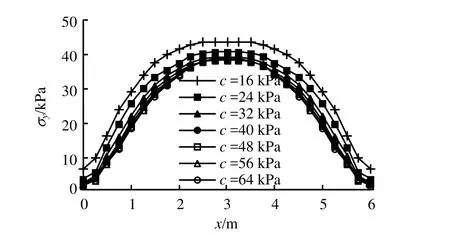
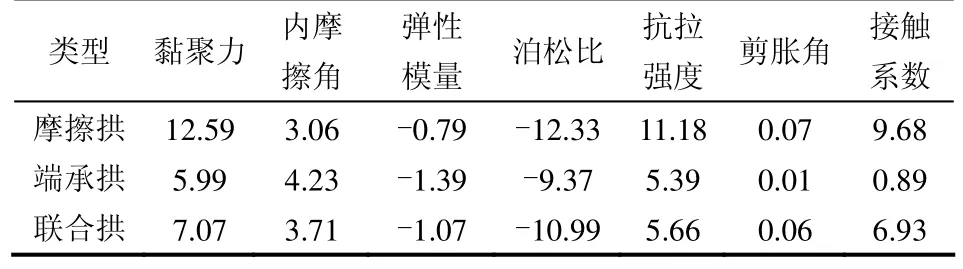
土拱极限状态的判定可采用 y向位移突变判据[12]。选取桩前横剖面中点(图1中A点)为监测点，可得其δy-q关系曲线如图8所示。由曲线转折点（1～3）可确定3种拱的极限承载力依次约为：q1=56 kPa，q2=104 kPa，q3=148 kPa。由 q3

图8 3种模型中监测点的δ y-q曲线Fig.8 δ y-q curves of monitored points of three models

土拱破坏历程可由塑性区的开展情况反映。极限荷载作用下，当模拟运行至一半时间步和全部时间步时，截取桩周有塑性区开展的网格部分(仅左半部分)如图9所示。由图可知，摩擦拱的塑性区分布在平行于桩侧线的邻域内，端承拱塑性区则围绕桩周开展，尤其在桩背处范围较大。联合拱塑性区可近似为两单拱的叠加，且率先从桩侧与桩背交角处产生，然后向桩前和桩后交替发展，直至桩前处先形成塑性贯通区，最终才到桩背处贯通。因此，在联合拱中，摩擦拱先破坏，端承拱后破坏，期间两者交替进行。且就破坏类型而言，桩背附近以剪切破坏为主(深色)，桩侧及桩前处则以受拉破坏为主(浅色)。

图9 3种拱在极限状态下的塑性区分布Fig.9 Distributions of plastic zones of three arches under limit state

4 土拱强弱影响因素及规律

4.1 影响因素分析

桩间距和桩截面尺寸是影响土拱强弱的控制因素[13]，但由前面建模可知，L、a、b在不同模型中存在自身尺寸制约，难于同比研究，故此处仅以土体性质参数作为目标因素，研究其对土拱强弱的影响规律。

采用单因素分析法进行研究。以表1的材料参数值为基准，各因素依次按指定的变化率取不同值，其余因素值保持不变，进行模拟研究。这里因素变化率向量统取[-0.6 -0.4 -0.2 0 0.2 0.4 0.6]。土拱强弱用桩的荷载分担比ξ来评价，ξ越大，表明拱效应越强。ξ=1-Pr/Pt，其中Pt为滑坡总推力且Pt=qL，Pr为桩前剩余推力，可由桩前横剖面处σy分布曲线与x轴所围面积表示[14]。考察到q对ξ影响较大，3种模型中q分别取对应极限荷载值的1/2。

以研究黏聚力c对联合拱强度的影响为例，分析信息如表2，其中组号4所在行为基准算例。取表中不同c值分别进行模拟，可得桩前横剖面处σy分布曲线如图10所示，据此算出对应的ξ值及其变化率，绘制出变化率关系曲线如图11所示。由曲线变化趋势可直观反映黏聚力因素对联合拱强度的影响。不同目标因素对3种拱影响的分析过程与此相同。

表2 联合拱受黏聚力影响分析表Table 2 Effects of cohesion on united arch

图10 联合拱模型桩前横剖面处σ y分布Fig.10 Distributions of σ y of cross-section in the front of piles of united arch

图11 联合拱受黏聚力影响Fig.11 Effect of cohesion on united arch

4.2 影响规律分析

按上节方法，可得3种模型中不同目标因素对应的变化率关系曲线如图12所示。

图12 土体参数对3种拱的影响Fig.12 Effects of soil parameters on three arches

为方便描述，采用曲线的平均斜率k来衡量目标因素对土拱强度的影响。显然k为正时，表示因素值增大对土拱增强起积极作用，反之起消极作用；k值绝对值越大，表示影响程度越大。据图12将各曲线对应的k值统计如表3所示。

表3 曲线平均斜率k(/%)Table 3 Average slope k of curves(/%)

定性分析目标因素对土拱强度的影响性质。表3同一列中k值的正负号均相同，表明同种因素对3种拱的影响性质完全一致，且有：黏聚力、摩擦角、抗拉强度、剪胀角和桩土接触系数对土拱强度产生积极影响；弹性模量、泊松比则产生消极影响。若只取联合拱情况，该结论与文献[15]等基本一致。

定量分析目标因素对土拱强度的影响程度。由表3中每行可知，不同因素对同一拱的k值均不同，如对摩擦拱，各因素按k的绝对值大小排序为：黏聚力>泊松比>抗拉强度>接触系数>摩擦角>弹性模量>剪胀角，因素排序越前，表明对拱强度影响越大。同理可对另两拱进行分析，显然不同拱中各因素排序不同；由表中每列可知，同种因素对不同拱的k值也不同，如对黏聚力因素，不同拱按k的绝对值大小排序为：摩擦拱>联合拱>端承拱，拱排序越前，表明拱强度对因素越敏感。同理可对其他因素进行分析，显然不同因素中各拱的排序也不同。

联合拱k值皆处于两单拱之间，体现了两单拱的有机联合，其与两单拱k值的接近程度，反映了因素影响联合拱的具体路径。如本例中桩土接触系数对联合拱的k值较接近摩擦拱相应值，表明该因素主要通过影响摩擦拱来影响联合拱。同理可分析其他因素影响联合拱的具体路径。

5 结 论

（1）联合拱的发育以摩擦拱最先形成开始，以端承拱最终破坏结束，期间两单拱并存且有各自的主导区域，这是土拱最基本的发育历程及分布特点，该结论与室外大型模型试验结果一致[16]

（2）联合拱的分布区域、极限承载力和塑性区分布皆可近似由两单拱叠加所得，从而为联合拱可拆分为两单拱研究提供了理论支持和路径。上述构成中，相对摩擦拱而言，端承拱所占比例较大，因而属支配部分。

（3）不同因素对同种拱的影响性质及影响程度均存在差异，同一因素对不同拱的影响性质一致但影响程度不同。认识到影响规律方面的差异性及具体路径,有助于改善目前该方面结论过于笼统的局面。

（4）文中结论与基准算例参数的具体取值密切相关，不一定具有普适性，仅旨在提供研究土拱效应的新思路。且目前暂未有现成实例进行对比验证，后续工作应开展相应的模型试验加以研究。

[1]TERZAGHI K. Theoretical soil mechanics[M]. New York:John Wiley & Sons, 1943.

[2]李长冬. 抗滑桩与滑坡体相互作用机理及其优化研究[D]. 北京: 中国地质大学, 2009.

[3]黄新文. 桩后土拱与桩间土拱联合作用探讨[J]. 四川建筑, 2006, 26(6): 76－79.

[4]吕庆, 孙红月, 尚岳全. 抗滑桩桩后土拱效应的作用机理及发育规律[J]. 水利学报, 2010, 41(4): 471－476.LÜ Qing, SUN Hong-yue, SHANG Yue-quan.Mechanism and development law of soil arch effect behind anti-slide piles[J]. Journal of Hydraulic Engineering, 2010, 41(4): 471－476.

[5]韩爱民, 肖军华, 梅国雄. 被动桩中土拱效应特征与影响参数研究[J]. 工程地质学报, 2006, 14(1): 111－116.HAN Ai-min, XIAO Jun-hua, MEI Guo-xiong. Behavior of soil arching between passive piles and effects parameters study[J]. Journal of Engineering Geology,2006, 14(1): 111－116.

[6]周应华, 周德培, 冯君. 推力桩桩间土拱几何力学特性及桩间距的确定[J]. 岩土力学, 2006, 27(3): 455－458.ZHOU Ying-hua, ZHOU De-pei, FENG Jun.Geometrically mechanical characters of soil arch between two adjacent laterally loaded piles and determination of suitable pile spacing[J]. Rock and Soil Mechanics, 2006,27(3): 455－458.

[7]张建勋, 陈福全, 简洪钰. 被动桩中土拱效应问题的数值分析[J]. 岩土力学, 2004, 25(2): 174－184.ZHANG Jian-xun, CHEN Fu-quan, JIAN Hong-yu.Numerical analysis of soil arching effects in passive piles[J]. Rock and Soil Mechanics, 2004, 25(2): 174－184.

[8]贾海莉, 王成华, 李江洪. 关于土拱效应的几个问题[J].西南交通大学学报, 2003, 38(4): 398－402.JIA Hai-li, WANG Cheng-hua, LI Jiang-hong. Discussion on some issues in theory of soil arch[J]. Journal of Southwest Jiaotong University, 2003, 38(4): 398－402.

[9]刘赪炜, 韩煊. 单桩数值模拟参数与方法的研究[J]. 岩土工程学报, 2010, 32(增刊2): 204－207.LIU Cheng-wei, HAN Xuan. Method and parameters of numerical simulation on single pile[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(Supp. 2): 204－207.

[10]RCHARD L H. The arch in soil arching[J]. Journal of Geotechnical Engineering, 1985, 111(3): 302－318.

[11]杨明. 桩土相互作用机理及抗滑加固技术[D]. 成都:西南交通大学, 2008.

[12]刘金龙, 栾茂田, 赵少飞, 等. 关于强度折减有限元方法中边坡失稳判据的讨论[J]. 岩土力学, 2005, 26(8):1345－1348.LIU Jin-long, LUAN Mao-tian, ZHAO Shao-fei, et al.Discussion on criteria for evaluating stability of slope in elastoplastic FEM based on shear strength reduction technique[J]. Rock and Soil Mechanics, 2005, 26(8):1345－1348.

[13]杨明, 姚令侃, 王广军. 桩间土拱效应离心模型试验及数值模拟研究[J]. 岩土力学, 2008, 29(3): 817－822.YANG Ming, YAO Ling-kan, WANG Guang-jun. Study of centrifuge model tests and numerical simulation on soil arching in space of piles[J]. Rock and Soil Mechanics,2008, 29(3): 817－822.

[14]胡焕校, 刘静, 吴海涛, 等. 抗滑桩桩后土拱效应特征三维数值研究[J]. 工业建筑, 2010, 40(3): 88－93.HU Huan-xiao, LIU Jing, WU Hai-tao, et al.Three-dimensional numerical analysis of soil arching effect surrounding anti-slide pile[J]. Industrial Construction, 2010, 40(3): 88－93.

[15]刘静. 基于桩土共同作用下的抗滑桩的计算与应用研究[D]. 长沙: 中南大学, 2007.

[16]董捷. 悬臂桩三维土拱效应及嵌固段地基反力研究[D].重庆: 重庆大学, 2009.