三轴试验抗剪强度参数值回归分析法的区别与修正

余东明，姚海林，吴少锋

（1. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071；2. 广东电网公司佛山南海供电局，广东 佛山 528200）

1 引 言

岩土的三轴压缩试验是确定岩土抗剪强度参数黏聚力c和内摩擦角φ值的重要方法。试验直接获得轴向破坏强度σ1和对应的围压σ3，分别称为大、小主应力，规范给出采用拟合出 σ1-σ3最佳曲线或基于强度准则拟合破坏包线，再推导出c、φ值的方法[1－3]。以往拟合曲线多采用手工作图形式，存在较大随意性。为了得到较为准确的 c、φ值，现在的岩土工作者倾向在试验数据的基础上采用较严谨的数学理论进行推导或利用软件分析，以避免由于手工作图产生的随意误差。刘善均等[4]依据破坏应力圆与强度包线尽可能相切，基于最小二乘法推导了求解 c、φ值的方程组，并编制计算机程序来求解方程组。Zambrano-Mendoza等[5]提出用应力圆圆心到强度包线距离进行最小二乘法回归拟合时，应同时考虑破坏面正应力和剪应力的误差。陈立宏等[6－7]推导了两种使用线性回归理论求解c、φ值的方法，指出了这两种方法不同之处并初步分析了其原因。阮波等[8]根据非线性规划理论，应用EXCEL软件对三轴试验的强度包线直接进行规划求解获取了抗剪强度参数值。本文在Mohr-Coulomb强度准则的假设下，深入最小二乘法的线性回归原理，分析了两种最常用的三轴试验 c、φ值确定方法。揭示了这两种方法结果差异的根本原因，提出了一种修正方法并从理论与实际两方面对其进行了验证。为合理确定岩土三轴试验抗剪强度参数值提供依据。

2 经典最小二乘法的一元线性回归

对样本数据(xi，yi)，若存在yi=a+bxi+εi，并假定：

（1）误差 εi是数学期望值为 0、方差不变的随机变量，即 E(εi)=0，Var(εi)不变；

（2）xi为非随机变量。

则使

满足式（1）的a，b值是回归方程y = a + bx的回归系数的最佳线性无偏估计量，此时：

其中： Lxx、 Lyy与Lxy含义相同。

这就是经典最小二乘法的一元线性回归计算方法[9－10]。这种方法的最小二乘估算结果最为理想，计算简单、且易于理解，已成为线性回归最常用的方法。

3 三轴试验抗剪强度参数的两种回归方法

在进行岩土三轴试验数据分析时，假设岩土的剪切破坏强度满足Mohr-Coulomb准则：

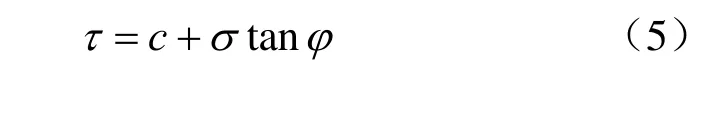
利用三轴试验测量数据，基于线性回归的原理求解出抗剪强度参数c、φ值，常采用两种方法。

3.1 σ1-σ3法

利用破坏应力圆由式（5）可推导出

其中，

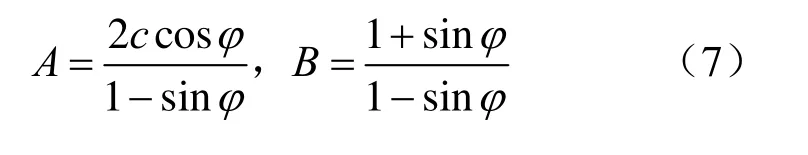
岩土三轴试验直接测得试样的大小主应力σ1i和σ3i，所以可以依据线性回归原理直接对(σ3i，σ1i)数据进行最小二乘法线性回归，得到A、B值，再利用式（7）可以计算出c、φ值。这种方法在文献[6]中被称为“σ1-σ3法”。

3.2 p-q法

注意到式（6）可以变换为

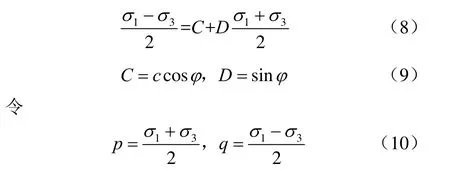
则式（8）变为

则可以建立p-q坐标系统，将三轴试验测量数据对（σ3i，σ1i）转化为（pi，qi）数据，再依据线性回归原理对得到的（pi，qi）数据进行最小二乘法线性回归，可以得到C、D值，利用式（9）也可以计算出c、φ值。这里的p、q实际上就是σ3-σ1坐标系下破坏应力圆的圆心横坐标和半径。这种方法在文献[6]中被称为“p-q 法”。

3.3 “σ1-σ3法”和“p-q法”的区别

“σ1-σ3法”和“p-q法”都可以应用最小二乘法进行线性回归求出回归系数，再利用回归系数与抗剪强度参数的关系式求解出c、φ。还可以看出“p-q法”的回归方程形式是直接由“σ1-σ3法”的回归方程形式推导出来的。从这个意义上说，“p-q法”和“σ1-σ3法”求出的抗剪强度参数值应该是一样的。而文献[6]无论从理论推导上还是从试验结果的分析上都明确得出二者的抗剪强度参数值并不相同，文献对此进行了分析，认为是σ1的误差导致了二者的差别，并认为“σ1-σ3法”的结果更为准确，但没有揭示导致二者差别的根本原因。

σ1和σ3是岩土三轴试验的测量值。其中σ3是试件所受围压，是试验前设定好的值，在试验过程中σ3的水平是受到控制的，可忽略误差认为是固定值。而σ1是在试验过程中测量出的破坏强度值，是无法控制的，认为其误差不可忽略，假定是数学期望值为0、且方差不变的随机变量，即：

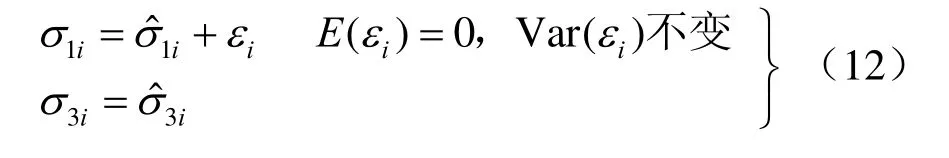
用“σ1-σ3法”进行线性回归，则

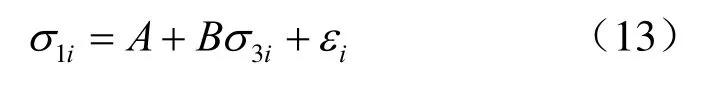
可以看出，“σ1-σ3法”完全符合经典最小二乘法线性回归的假设和形式，故“σ1-σ3法”所得到的A、B估值是A、B真值的最佳解，因而由此推算出的c、φ值也应是c、φ真值的最佳解。

由式（12）可得

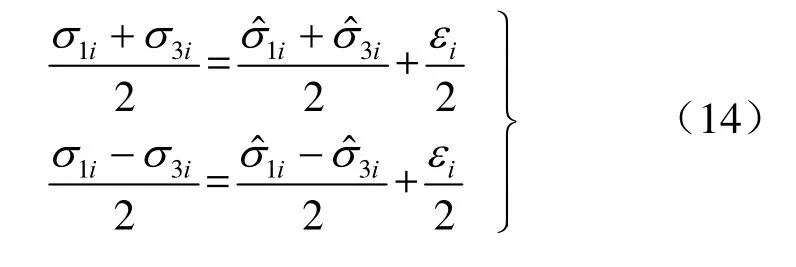
即，

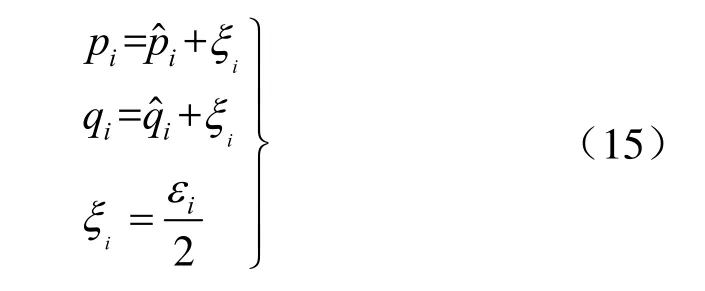
此时需要回归的数据中不仅因变量的测量值qi具有随机误差ξi，而且自变量的测量值pi也具有随机误差ξi，即pi也是随机变量。这违反了经典最小二乘法进行线性回归的前提假设，即自变量观测值为非随机变量。这时基于经典的最小二乘法进行线性回归已经不可用。

但“p-q法”仍然采用经典最小二乘法进行线性回归，实际上是强行消除自变量的误差，从式（15）可以看出，自变量的误差与因变量的误差是等量的，若因变量误差不能忽略也就等价于自变量误差同样不能忽略。强行忽略自变量误差的做法必然导致所得到的回归系数C、D不是C、D真值的最佳解，而由此推算出的c、φ值也不是c、φ真值的最佳解，所以会与“σ1-σ3法”得到的c、φ值不同。

“p-q法”回归方程的自变量含有 σ1，从而将 σ1的测量误差引入了自变量，违反了经典最小二乘法线性回归的基本假定，必然导致回归结果出现偏差。这就是两种方法的根本区别，也是文献[6]中用两种方法所得到的抗剪强度参数值不同的根本原因。而“σ1-σ3法”则完全满足经典最小二乘法线性回归的假定和形式。可以认为“σ1-σ3法”的回归结果是最接近真实值的，得出的c、φ值也是最接近真实值的。所以对三轴试验的σ1、σ3直接拟合得到抗剪强度参数值是最合理的。

4 对“p-q 法”的修正

由前述的分析可以看出，“p-q法”违反了经典最小二乘法线性回归的基本假定，使结果出现偏差。若σ1的误差可以忽略的话，无论“σ1-σ3法”还是“p-q法”得到的回归系数都将是真值，两种方法的回归方程将完全等价，此时这两种方法得到抗剪强度参数值完全一样。但实际上σ1的误差一般不能忽略，故从根本上说“p-q法”利用经典最小二乘法进行线性回归是错误的。应只考虑用“σ1-σ3法”计算c、φ值。然而在岩土三轴试验规范[1－2]中规定可利用p-q坐标系统分析抗剪强度参数值，故人们也习惯于“p-q 法”。

“p-q法”虽然符合三轴试验结果分析的习惯，但得到的结果有偏差，并非最佳解，甚至根本上说是错误的，因此，必须要对其修正。结合前面的分析可以认为，“σ1-σ3法”得出的抗剪强度参数值是最合理的，并且是唯一的。而“p-q法”违反了经典最小二乘法线性回归的基本假定，因此，若要修正“p-q法”就是要修正（pi，qi）线性回归的方法使得从中得到的抗剪强度参数值与“σ1-σ3法”完全一致。

4.1 正交最小二乘法的基本原理

当xi，yi均为随机变量，即：

对这种情况下的(xi，yi)进行一元线性回归，可以采用Golub和Van Loan对经典最小二乘法的推广，认为其基本依据应是使x方向及y方向的误差总平方和最小：

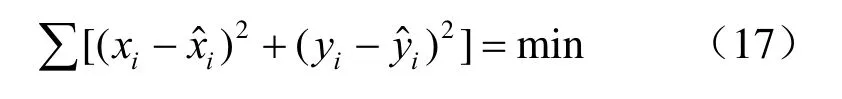
即，

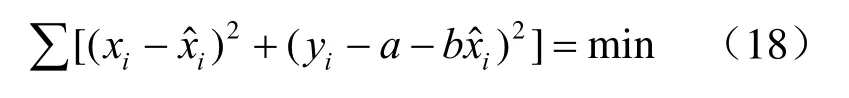
得到的a、b值，是同时考虑x和y两个方向误差的最佳估值。这里所推广的最小二乘法被称为整体最小二乘法[11]，也被称之为正交最小二乘法[12]。

4.2 修正的“p-q法”的线性回归系数

当用x代替σ3，y代替σ1，由式（6）、（10）得：

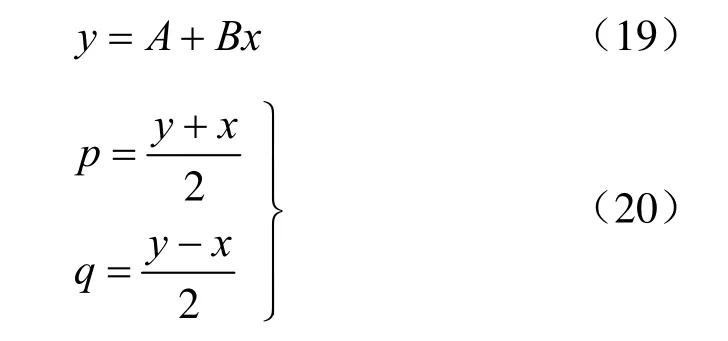
由式（15）可知，pi和qi都是随机变量，首先违反了经典最小二乘法关于自变量为非随机变量的前提假设；且pi、qi这两个随机变量的误差项都是εi，也违反了正交最小二乘法关于自变量和因变量的误差项要相互独立的前提假设。故既不能采用经典最小二乘法也不能采用正交最小二乘法对（pi，qi）进行线性回归。

但注意到此时情况与正交最小二乘法的回归比较接近，即自变量和因变量都是随机变量，故决定在正交最小二乘法的基础上进行修正，提出：

当xi、yi均为随机变量，即

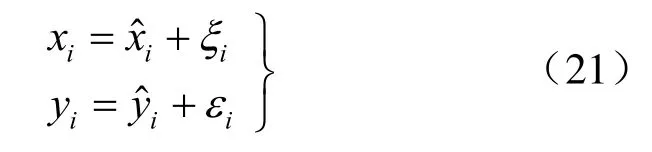
前提条件为：εi、ξi是相关联的，即二者非独立；E(εi)= E(ξi)= 0；Var(εi)= Var(ξi)为不变值。

对这种情况下的(xi，yi)进行一元线性回归，认为其基本依据应是使下式成立：

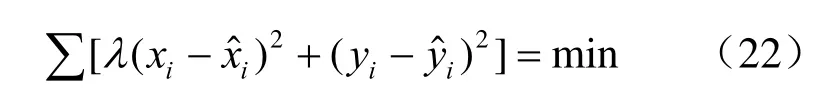
在式（22）中引入常数λ是用来表示因 xi、yi的误差不独立所带来的影响，暂且称λ为误差非独立影响系数。若能通过 xi、yi的误差关系求解出常数λ的话，代入式（22）则可得出(xi，yi)的一元线性回归系数。称这种方法为修正的正交最小二乘法。

可以看出，（pi，qi）刚好可以满足上述提出的修正的正交最小二乘法的前提条件，由式（15）还可以得到 pi、qi这两个随机变量的非独立关系是二者的误差项完全相同。基于本文提出的修正的最小二乘法进行（pi，qi）的线性回归的方法，本文称之为修正的“p-q法”。

由式（22）可得

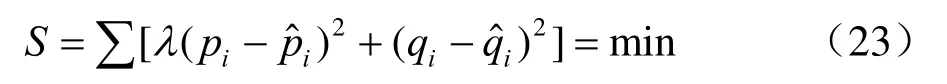
即，

若能根据式（24）得到的C、D值的话，则修正的“p-q法”将可用于岩土抗剪强度指标的分析。

由式（24）得：

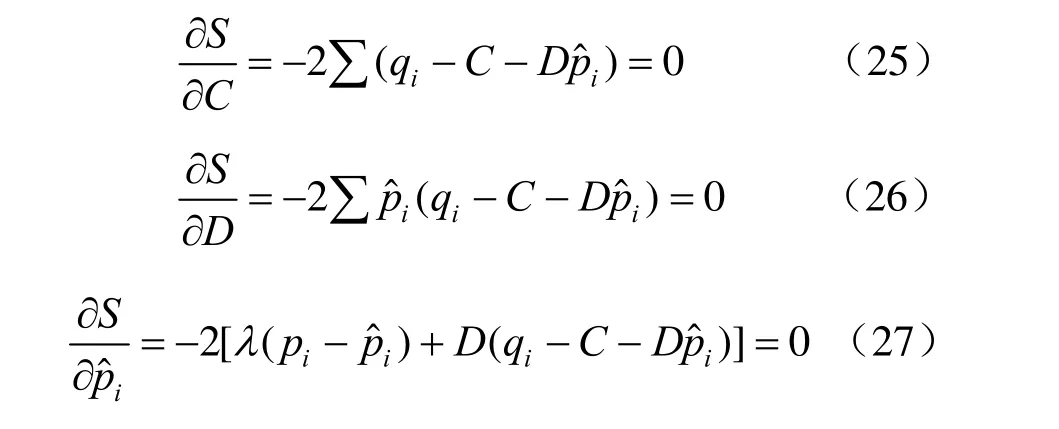
其中， i =1, 2, …,n。

由式（15）得：

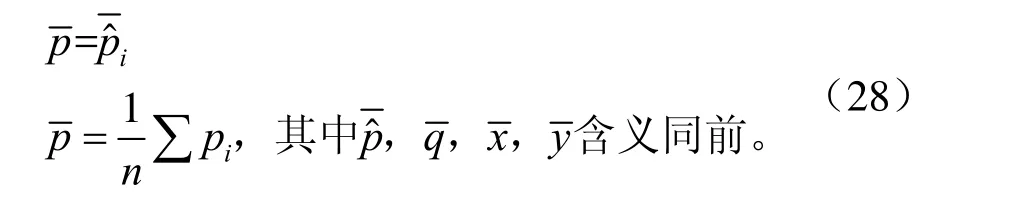
由式（25）、（26）并注意到式（28），得：

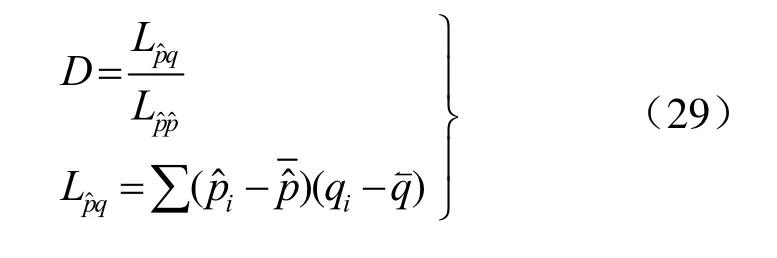
由式（27）、（28）、（30）得：

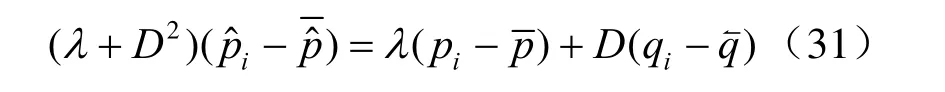
由式（31）可得：

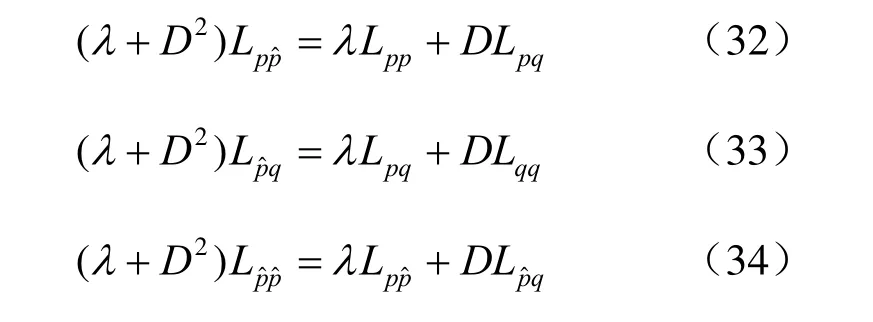
由式（31）～（33）及（28）得：

可得

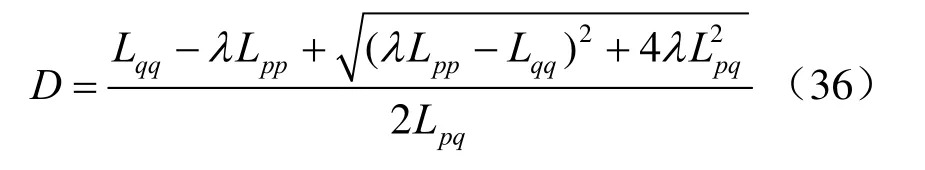
由式（30）、（31）可得

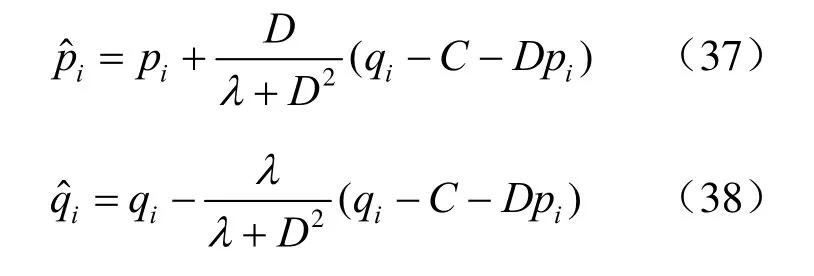
由式（15）知 pi、qi误差项相等，结合式（36）～（38）可得

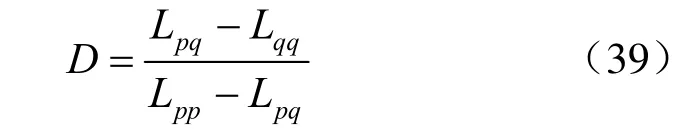
则

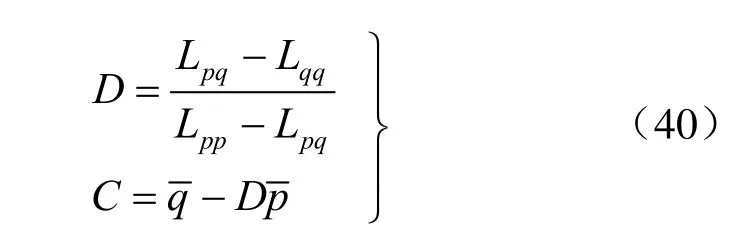
式（30）即为修正的“p-q法”的线性回归系数，再利用式（9）就可得到c、φ的最佳估值。

4.3 修正的“p-q法”与“σ1-σ3法”等效

修正的“p-q法”得出的c、φ如果是真值的最佳估值的话，那么它们应与“σ1-σ3法”得出的c、φ估值完全一致，即无论采用何种方法，c、φ最佳估值只有一组。若修正的“p-q法”与“σ1-σ3法”等效，则由式（7）、（9）可得：

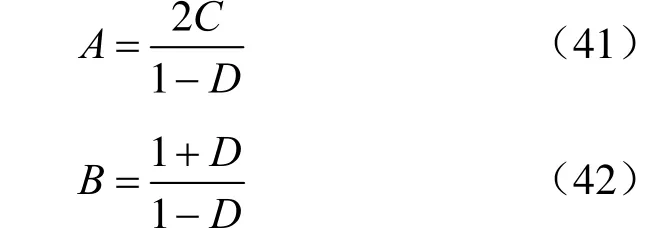
故若能证明“σ1-σ3法”的回归系数A、B值与修正的“p-q 法”的回归系数 C、D 值满足式（41）、（42），则即证明了修正的“p-q法”和“σ1-σ3法”等效。

由式（39）可得

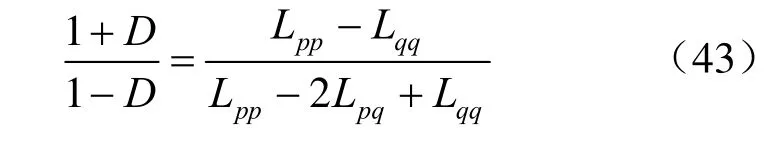
注意到式（29），由式（20）可得：

需要注意的是，这里x =σ1，y =σ1。

将式（44）代入（43）可得：

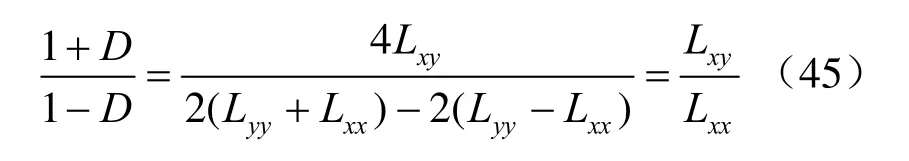
对式（19）利用经典的最小二乘法进行回归，由式（2）可得

由式（45）、（46）可知，式（42）成立，同理可证式（41）也成立。故修正的“p-q法”与“σ1-σ3法”是等效的得证。修正的“p-q法”得出和“σ1-σ3法”同样的c、φ值，它们是最合理的估值。

5 计算实例

四川省某拟建隧道围岩主要为千枚岩，对其进行室内三轴强度试验，取天然含水状态下的一组三轴试验数据，如表1所示。

分别采用“σ1-σ3法”和修正的“p-q法”确定抗剪强度参数c、φ值。

表1 天然状态下千枚岩三轴强度试验数据Table 1 Triaxial test data of phylliteunder natural state

（1）σ1-σ3法

由式（2）、（3）可得 B=4.61，A=49.06，则回归方程为

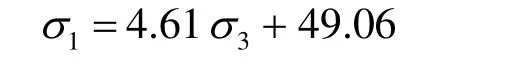
将A、B值代入式（7），求解可得：c = 11.42 MPa，φ = 40.06º。

（2）修正的“p-q 法”

由式（40）可得D = 0.64，C = 8.74，则回归方程为

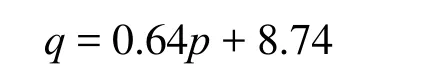
将 C、D 值代入式（9），求解可得：c= 11.42 MPa，φ = 40.06º。

可以看出“σ1-σ3法”和修正的“p-q法”计算出的抗剪强度参数值完全一致。

6 结 论

（1）从本质上揭示了两种线性回归方法得出的三轴试验抗剪强度参数值不一致的原因。指出“p-q法”由于自变量为随机变量，违背了经典最小二乘法线性回归的基本假定，因而得到的结果不可靠；而“σ1-σ3法”则完全满足经典最小二乘线性回归法的假定和形式，所得出的结果是真值的最佳估值。

（2）参考正交最小二乘法的原理，对“p-q法”提出修正的最小二乘法形式。使“p-q法”的自变量和因变量同为随机变量、且误差项不独立的前提条件在修正的最小二乘法中得到满足。称之为修正的“p-q法”并推导了修正后的回归系数。从理论上证明了修正的“p-q法”与“σ1-σ3法”得到的抗剪强度参数值完全一致，给出的一个实际算例也验证了这两种方法得到的c、φ值相同。

[1]南京水利科学研究院. SL237-1999 土工试验规程[S].北京: 中国水利水电出版社, 1999.

[2]交通部公路科学研究院. JTG E40-2007 公路土工试验规程[S]. 北京: 人民交通出版社, 2007.

[3]中国水电顾问集团成都勘测设计研究院. DL/T 5368-2007 水电水利工程岩石试验规程[S]. 北京: 中国电力出版社, 2007.

[4]刘善均, 王韦, 许唯临. 莫尔圆求解 c、φ值的最佳拟合[J]. 四川大学学报（工程科学版）, 2002, 34(6): 40－42.LIU Shan-jun, Wang Wei, XU Wei-lin. The optimal fitting method for computing c、φ using circle of Mohr[J].Journal of Sichuan University (Engineering Science Edition), 2002, 34(6): 40－42.

[5]ZAMBRANO-MENDOZA O, VALKO P P, RUSSELL J E. Error-in-variables for rock failure envelope[J].International Journal of Rock Mechanics and Mining Sciences, 2003, 40(1): 137－143.

[6]陈立宏, 陈祖煜, 李广信. 三轴试验抗剪强度指标线性回归方法的讨论[J]. 岩土力学, 2005, 26(11): 1785－1789.CHEN Li-hong, CHEN Zu-yu, LI Guang-xin. Discussion of linear regression method to estimate shear strength parameters from results of triaxial tests[J]. Rock and Soil Mechanics, 2005, 26(11): 1785－1789.

[7]陈立宏, 陈祖煜, 李广信. 线性回归抗剪强度指标方法的改进[J]. 岩土力学, 2007, 28(7): 1421－1426.CHEN Li-hong, CHEN Zu-yu, LI Guang-xin. A modified linear regression method to estimate shear strength parameters[J]. Rock and Soil Mechanics, 2007, 28(7):1421－1426.

[8]阮波, 张向京, 彭意. Excel规划求解三轴试验抗剪强度指标 [J]. 铁道科学与工程学报, 2009, 6(5): 57－60.RUAN Bo, ZHANG Xiang-jing, PENG Yi. Programming solver tools of Excel evaluate shear strength parameters from results of triaxial tests[J]. Journal of Railway Science and Engineering, 2009, 6(5): 57－60.

[9]张小蒂. 应用回归分析[M]. 杭州: 浙江大学出版社,1991: 78－82.

[10]G. A. F. 塞伯. 线性回归分析[M]. 北京: 科学出版社,1987: 125－128.

[11]黄开斌, 俞锦成. 整体最小二乘问题的解集与极小范数解[J]. 南京师大学报（自然科学版）, 1997, 20(4): 1－5.HUANG Kai-bin, YU Jin-cheng. Solution sets and minimum norn solution for the basic total least squares problem[J]. Journal of Nanjing Normal University(Natural Science), 1997, 20(4): 1－5.

[12]李玉武, 刘咸德. 正交最小二乘法及其在分析化学中的应用[J]. 矿岩测试, 2001, 20(4): 257－262.LI Yu-wu, LIU Xian-de. Orthogonal least squares method and its application in analytical chemistry[J]. Rock and Mineral Analysis, 20(4): 257－262.