干式变压器箔绕导体三维涡流场与附加损耗的数值仿真研究

王建民，景崇友，韩冬杰，单东雷，范亚娜，侯建江

(1.保定天威集团有限公司 技术中心，河北 保定 071056;2.华北电力大学 电气与电子工程学院，河北 保定 071003)

0 引言

干式变压器具有环保、防潮、阻燃和防腐蚀等特性，同时，干式箔绕变压器又以工艺制造机械化程度高与铁窗填充系数好和节能、省材为特点，因此，日益受到变压器制造企业与配电网用户的关注，其市场需求和容量在不断地增加。但是，由于干式变压器绕组漏磁场会在箔式绕组导体中产生极不均匀的涡流和涡流损耗，尤其是随着变压器容量的不断增加，箔绕变压器漏磁场、附加损耗和温升问题会更加突出，而目前附加损耗传统的设计方法是以绕组直流电阻损耗乘系数确定，显然，该方法难以准确反映绕组布置结构和导体材料 (铜或铝，导线或箔导体)对绕组附加损耗分布特性的影响，而采用二维数值方法计算时[1～5]，绕组涡流或涡流损耗的分布也难以合理地反映，因此，对于较大容量的箔绕变压器负载损耗设计误差通常难以准确把握，以至于绕组温升和局部过热问题难以合理控制。为此，对干式变压器箔绕导体开展三维涡流场与附加损耗等分布特性的数值应用研究，将具有十分重要的现实意义。

1 计算模型和场—路耦合的实现

1.1 计算模型与等效电路

所分析的典型干式变压器为多层园筒式双绕组结构，其排布顺序为:铁心-低压-高压，该类产品的低压绕组采用铜箔或铝箔 (其截面厚度约为2 mm，长度等于绕组高度)，并用轴向气道将绕组分为3～4层，而高压绕组采用普通扁导线，在轴向上分为4段，并用轴向气道将绕组分为2层，三相绕组之间的电气连接为Y/△联结组。

根据干式变压器结构特点分析和绕组电气连接，干式箔绕变压器漏磁场、短路阻抗和附加损耗的计算涉及铁心材料、具有面积大且厚度薄的低压箔绕导体，因此，论文所要求解的是一个三维非线性涡流场问题。由于低压箔绕导体中具有负载运行工作电流和未知的不均匀分布涡流存在，而采用常规的有限元方法需要事先知道绕组中的电流分布[6]，为此，作者分别建立了三维涡流场简化计算模型和采用场—路耦合方法的等效电路模型，如图1和图2所示。其假定条件如下:

(1)根据计算目标要求和结构对称性，计算模型沿三相中心平面前后取二分之一，除中心对称平面外，其他边界取至铁心或绕组足够远的距离。

(2)低压绕组按径向层数分为4个安匝区，如图2a中的C1，C2，C3，C4分别表示低压a相由内 (靠近铁心)向外的各层绕组，同样，低压b相和c相的各层绕组参见图2a。

(3)高压绕组每相的内外层共分为6个安匝区，并认为各安匝分区的电流分布均匀，如图2b所示。

(4)激励绕组和短接绕组的总安匝保持平衡;铁心按非线性、各向同性材料处理，忽略铁心涡流和磁滞的影响。

(5)认为三相电流对称，因此，等效电路中只有两个独立的电流源。

1.2 边值处理与场—路耦合的实现

根据上述假设条件，采用A-V-A组合位计算时，可将求解区域划分为涡流区 (矢量磁位A与标量电位V为求解量)和非涡流区域 (矢量磁位A为求解量)，其中低压箔绕导体和结构件为涡流区，而铁心、高压线匝导体可忽略涡流的去磁效应，因此，与周围介质一起构成非涡流区，对

应于A-V-A组合位求解干式变压器涡流场的有限元法边值问题为:在计算模型的对称面和所有外边界上，磁力线满足平行边界条件。

式中:JSh为高压绕组激励源电流密度，A/m2;v为磁阻率，m/H;σ为电导率，S/m;Jsl为低压绕组源电流密度，可以用感应电势产生的电流in乘系数ki(与绕组匝数及面积有关)表示，即Jsl=ki·in。由如下的场—路耦合法绕组电路通用方程确定:

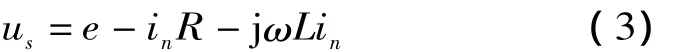
式中:us为激励绕组施加的电压;R，ωL分别为高压或低压绕组的电阻与电抗，Ω;n为绕组序号;e为高压或低压绕组的感应电势，V;是矢量磁位的函数 (ke是与绕组几何尺寸和匝数有关的感应电势系数)，其方程式表示为:

联立方程式 (1)至式 (4)，便可以得到场—路耦合方法的空间离散方程组[7，8]，进而求得干式变压器的绕组漏磁场分布和低压箔绕导体的电流分布和涡流损耗分布等参数。

2 附加损耗计算方法

干式变压器的附加损耗主要包括漏磁场在绕组导体中产生的涡流损耗和漏磁场在夹件、铁心等金属结构件中产生的杂散损耗，通常后者在干式变压器总附加损耗中所占的比例很小，因此，干式变压器绕组涡流损耗的计算，特别是低压箔绕导体的涡流场分布，已成为干式箔绕变压器附加损耗计算和性能优化的关键技术内容。

2.1 低压箔绕导体涡流与涡流损耗计算

低压箔绕导体中除了源电流之外，还要考虑感应涡流，利用场—路耦合法求得矢量磁位A和标量电位V之后，箔绕导体单元中的涡流密度Je和涡流损耗 Pe计算公式分别为[9，10]

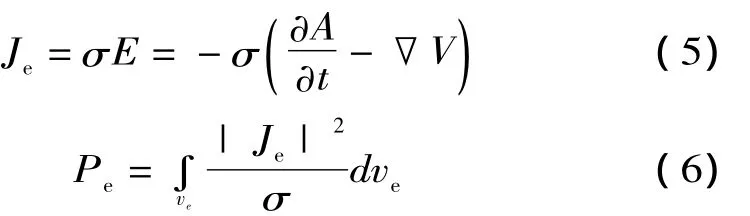
低压绕组总的涡流损耗为:

2.2 高压绕组导线涡流损耗的计算

对于由普通细导线组成的高压绕组，导体涡流和位移电流均可以被忽略，但涡流损耗需要考虑，并根据平板导体损耗计算方法，可以得到高压绕组涡流损耗计算公式如下[11]:

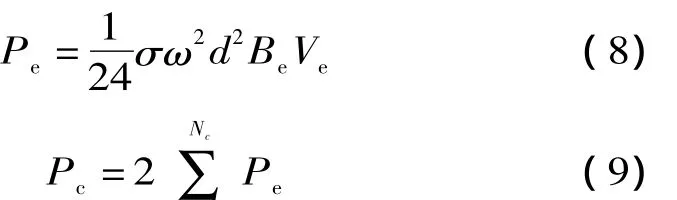
式中:Pe为绕组单元涡流损耗，W;Be为单元磁通密度，T;d为绕组导体截面尺寸，m;Ve为单元体积，m3;Pc为绕组总的涡流损耗，W;Nc为高压绕组单元总数。

3 数值计算结果与验证性分析

利用本文确定的计算模型与方法，分别对相同规格2 500 kVA/6 kV干式铜箔和铝箔变压器样机的绕组涡流场、短路阻抗和附加损耗等进行了数值计算与结构优化分析。根据研究结果确定了一种性价比较优的样机设计方案 (1-铝箔2-铜箔)和用于指导产品设计的分析结论。

3.1 绕组涡流场分布

图3为变压器绕组三维漏磁场分布，表1为箔绕导体电流密度计算结果，图4为低压绕组各层电流密度 (含涡流)沿绕组二分之一高度的分布，图5至图7分别为高低压绕组之间的轴向气道纵向磁通密度、方案1的低压绕组内层和高压绕组的径向磁通密度沿绕组高度的分布。

从图3至图7可以看出，绕组漏磁场分布上、下对称，纵向磁通密度沿本身高度呈波浪形分布，其最大值为0.051 3(T);低压绕组各层径向磁通密度沿本身高度的分布在绕组端部具有最大值，并且，靠近铁心的低压内层径向磁通密度大于其他各层，两方案的径向磁通密度最大值分别为0.027(T)和0.038(T);由于导体涡流主要由径向磁通密度产生和集肤效应作用，因此，对应的低压绕组各层涡流与涡流损耗在端部出现最大值 (图4所示)。从表1箔绕导体电流密度计算结果可知，由于导体材料电导率的影响，方案1的铝箔最大电流密度 (含涡流)是工作电流密度(不含涡流)设计值的6倍;而方案2的铜箔最大电流密度是工作电流密度值的10倍，因此，涡流与工作电流迭加后沿绕组高度极不均匀的电流分布在低压铜箔导体中，更易于产生损耗密度过大和局部过热问题。对于高压绕组由于受到本身段间气隙的影响，所以，纵向磁通密度沿绕组高度呈波浪形分布和高压绕组各层径向磁通密度沿本身高度的分布出现几个不同的峰值，两个方案的径向磁通密度最大值分别为0.015(T)和0.013 5(T)，并分别出现在靠近绕组端部的段间气隙附近和绕组端部，因此，由径向磁通密度在高压绕组对应的部位将产生较大的涡流损耗。

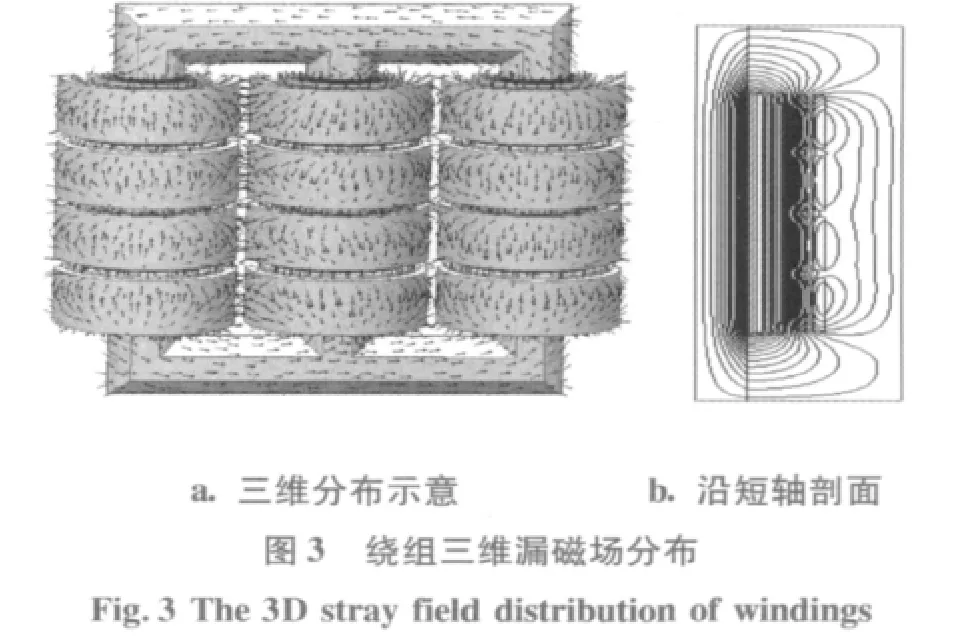
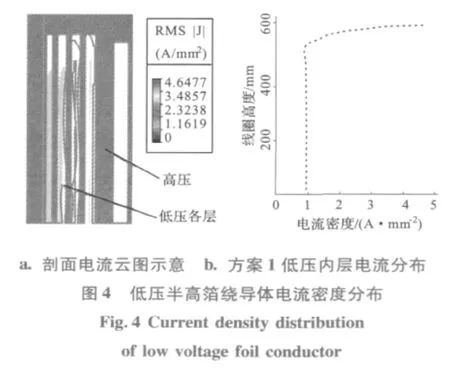
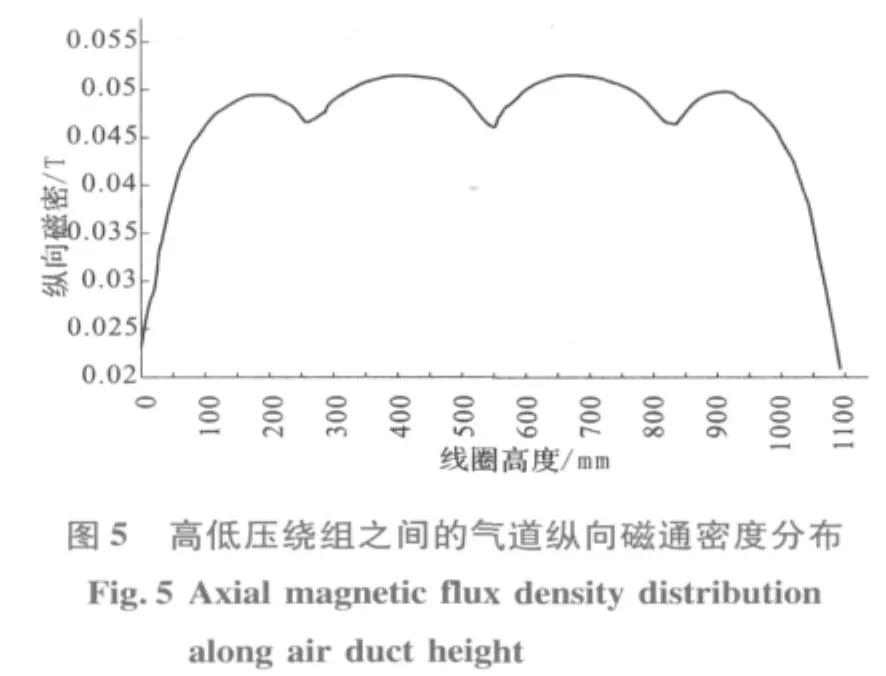
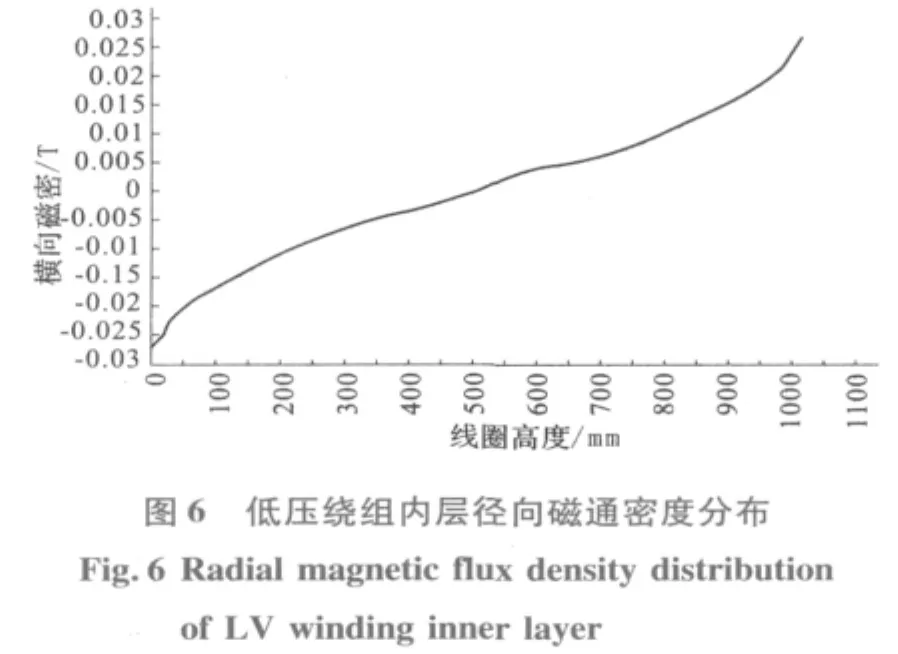
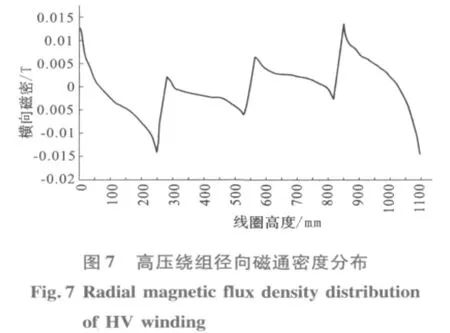
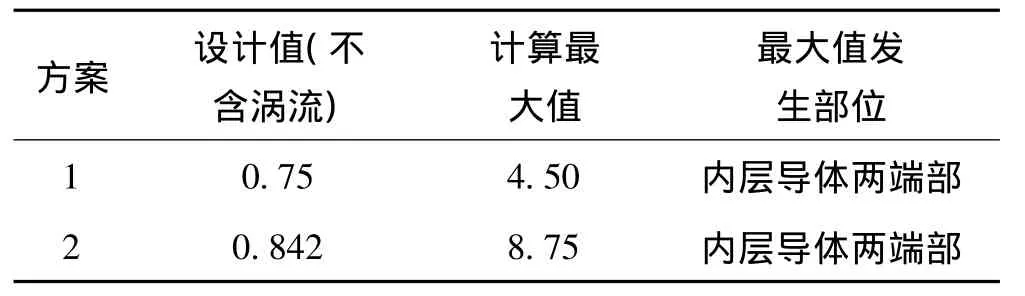
表1 低压箔绕导体电流密度结果Tab.1 Current density results of low voltage foil conductor(A/mm2)

3.2 短路阻抗

短路阻抗是变压器主要性能参数之一，利用磁场能量法可以得到干式变压器的短路阻抗，两台样机的短路阻抗结果如表2所示。由此可知，绕组短路阻抗计算值与实测值的相对误差在3%内，计算结果优于传统方法短路阻抗的设计值。

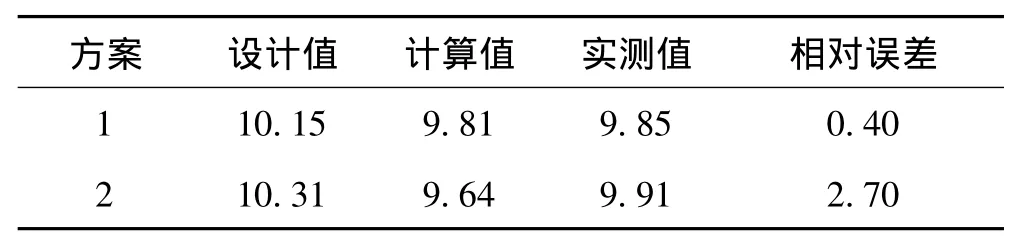
表2 变压器短路阻抗的比较结果Tab.2 Analysis results of short-circuit impedance(%)

3.3 绕组附加损耗及其分析验证

通过对干式变压器两个方案绕组涡流损耗的计算和结构优化分析，表明箔式绕组导体涡流损耗可达直流电阻损耗的20% ～65%，而普通导线绕组涡流损耗为5% ～20%，并确定了一种性能较优的结构设计方案;利用两个方案的样机负载损耗试验与计算结果，检验了附加损耗计算方法的合理性。

3.3.1 绕组附加损耗

表3给出了两个方案在120℃时的绕组附加损耗与单位体积最大损耗密度。从表3中的计算结果可知，两个方案的低压箔绕导体涡流损耗占直流电阻损耗的百分比分别为21.6%和62.9%，单位体积最大损耗密度分别为88.69(kW/m3)和112.0(kW/m3)，并且，出现在低压绕组内层两端部附近，这是由于绕组涡流损耗与磁通密度的平方成正比及绕组径向磁通密度分布结果所决定;而高压绕组导线涡流损耗与单位体积最大损耗密度，远小于低压箔绕导体对应的值，因此，低压箔式绕组较高压绕组易于产生局部过热，方案2比方案1情况较严重。

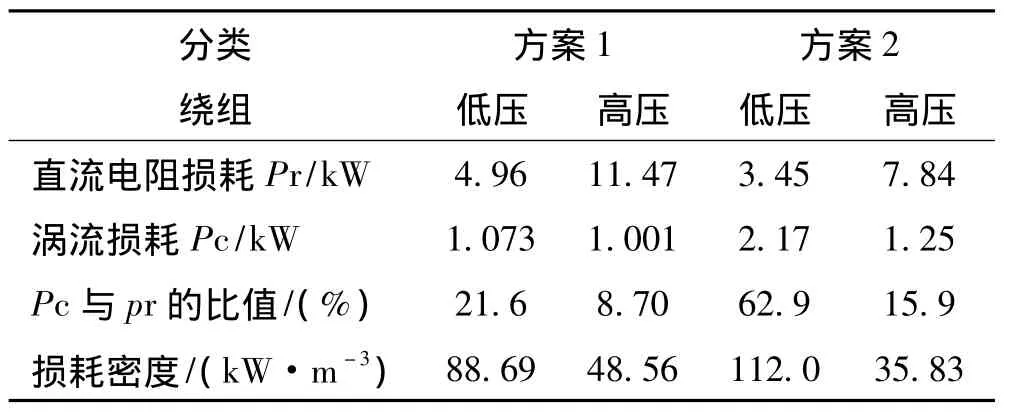
表3 绕组附加损耗计算结果Tab.3 Calculating results of winding additional losses

3.3.2 负载损耗

表4给出了两个方案在120℃时的负载损耗计算与实测结果，表中的负载损耗设计值是通过直流电阻损耗乘以经验系数的传统方法而得，计算值是把负载损耗分成直流电阻损耗、绕组涡流损耗与金属结构件杂散损耗 (与变压器容量和短路阻抗有关的解析公式确定)三部分相加而得。

从表4中的比较结果可知，两个方案的负载损耗计算结果与实测值相对误差约为5.0%，而方案2的负载损耗设计值误差在10.0%以上，由此说明了计算方法的有效性和准确计算箔绕导体附加损耗，对于预防干式变压器局部过热和提高产品性能可靠性的重要作用。

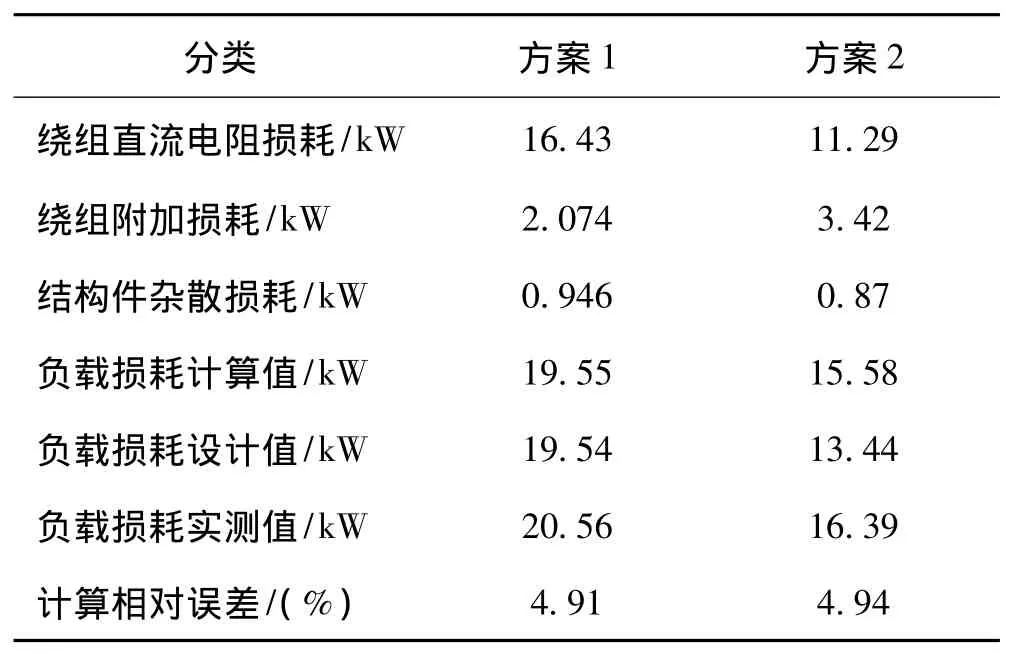
表4 负载损耗结果的比较Tab.4 Comparison of load loss results

3.3.3 对绕组结构与性能的优化分析

根据上述结果分析，在低压绕组两端部电流密度和体积损耗密度最大，为了改善漏磁分布和预防绕组局部过热，针对方案1在改变高压绕组高度而大于(工况1)、等于(工况2)和小于(工况3)低压绕组高度三种情况下，表5给出了绕组最大径向磁通密度、最大电流密度和涡流损耗等参数的计算结果。由此可知，随着高压绕组高度的降低，低压绕组相关场量逐渐减小，而高压绕组相关场量有所增大，因此，从预防产品局部过热角度考虑，工况3为最终确定的绕组结构。

综合全文分析结果，并考虑到该类型干式变压器绕组为浇注形式，因此，在绕组机械性能满足要求的情况下，方案1在经济性和预防绕组局部过热方面具有市场竞争优势。

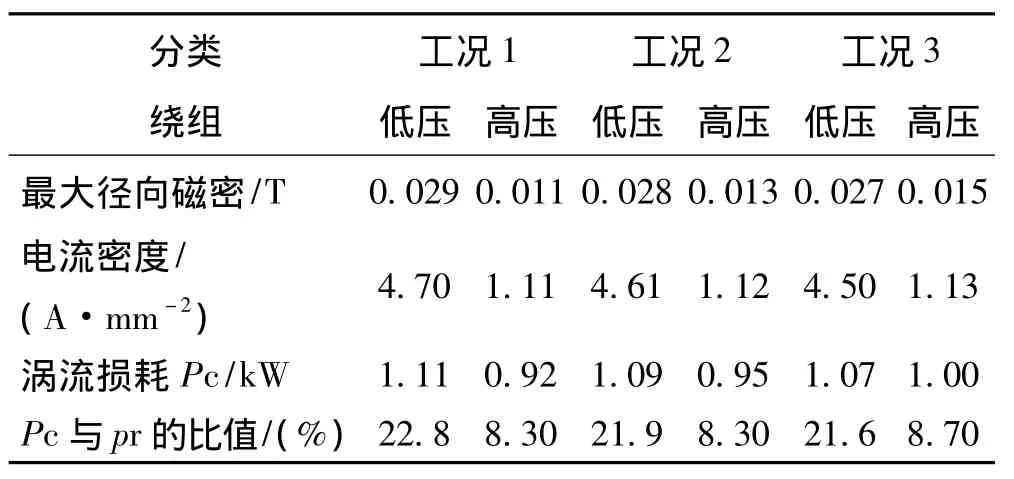
表5 绕组部分参数计算结果Tab.5 Calculating results of winding parameters

4 结论

针对典型干式变压器箔绕结构特点，作者建立了合理的计算模型和绕组涡流损耗计算方法。利用有限元场—路耦合方法，对铜、铝两个方案的绕组涡流场、短路阻抗和附加损耗进行了数值计算与优化对比分析，并根据分析结果确定了一种性价比较优的设计方案。通过短路阻抗与负载损耗的计算与产品测量结果的比较，验证了计算方法的有效性，从而，为干式变压器负载损耗的准确计算和预防局部过热提供了一种有效的分析方法。

[1]保定天威保变电气股份有限公司.电力变压器手册[M].北京:机械工业出版社，2003.

[2]尹克宁.变压器设计原理[M].北京:中国电力出版社，2003.

[3]程志光，高桥则雄，博扎德·弗甘尼，等.电气工程电磁热场模拟与应用[M].北京:科学出版社，2009.

[4]康真，张梅.一种新型变压器风冷控制系统的设计[J].电网与清洁能源，2010，26(10):23-25.Kang Zhen，Zhang Mei.A new design of transformer aircooled control system[J].Power System and Clean Energy，2010，26(10):23-25.

[5]景崇友，王建民，王永青，等.大型变压器漏磁场及特性参数的工程仿真软件研发[J].变压器，2008，45(4):1-5.Jing Chongyou，Wang Jianmin，Wang Yongqing，et al.Development of engineering simulation software of leakage field and characteristic parameters in large transformer[J].Transformer，2008，45(4):1-5.

[6]Wang Jianmin，Jing Chongyou，Fan Yana，et al.Numerical simulation of 3D stray field and short circuit impedance for a phase-shifting rectifier transformer[J].International Journal of Applied Electromagnetics and Mechanics，2010，33(1-2):191-196.

[7]谢德馨，杨仕友.工程电磁场数值分析与综合[M].北京:机械工业出版社，2009.

[8]颜威利，杨庆新，汪友华，等.电气工程电磁场数值分析[M].北京:机械工业出版社，2006.

[9]Eleftherios I Amoiralis，Pavlos S，Georgilakis，et al.Global transformer optimization method using evolutionary design and numerical field Computation[J].IEEE Trans On Magn，2009，45(3):1720-1723.

[10]刘东升，张俊杰，赵峰，等.特高压特大容量变压器三维涡流场计算和防止局部过热技术的研究[J].变压器，2009，46(9):1-5.Liu Dongsheng，Zhang Junjie，Zhao Feng，et al.3D eddy current field calculation and partial overheat protection technology research of UHV large transformer[J].Transformer，2009，46(9):1-5.

[11]杨素梅，程志光，朱晓荃.三维涡流场及屏蔽杂散损耗[J].电力系统及其自动化学报，2007，19(6):30-34.Yang Sumei，Cheng Zhiguang，Zhu Xiaoquan.Three dimensional eddy current field and stray loss in shields[J].Proceedings of the CSU-EPSA，2007，19(6):30-34.