基于EEMD与时间序列法的短期风电场功率预测
2012-09-19高亚静李均强
常 鹏,高亚静,张 琳,李均强
(华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引言
全球性的能源危机和气候变化,驱动了新能源在世界范围内的迅速发展和应用。风能作为一种可再生的、洁净的能源,得到了世界各国的高度重视。随着风力发电技术的发展进步以及政府对可再生能源事业的重视,国家更是加快速度投资建设风电,风力发电得到了突飞猛进的发展。但随着风电装机容量在电网装机容量中所占比例的增大,给电网带来了很大冲击,增加了电网运行的不确定性,给电网调度带了一系列的问题。此外由于电网缺乏前瞻性的规划和创新性的调度控制技术,电网对大规模风电的接纳能力很弱,导致电网经常限制风电出力,造成弃风损失。据初步统计,2010年下半年,由于缺乏具体的风电送出和风电消纳方案,国内风电能发电无法被电网消纳而弃风就达27.76亿kW·h。如何提高电网消纳风电的能力已成为当前风力发电大规模利用亟待解决的问题[1,2]。
要解决以上的问题,最首要的就是对风电场输出功率进行准确预测,这被认为是增加电网对风电的接纳能力、提高电力系统运行安全性与经济性的有效手段之一[3]。国内外对于风力发电包括功率预测等方面的研究不断深入,但关于风电场功率预测还有待进一步研究[4]。
目前,风电场功率预测的方法有卡尔曼滤波法 (Kalman filters)[5]、时间序列法 (time series method)[6,7]、人工神经网络法 (ANN)[8,9]、模糊算法 (FA)[10]、空间相关性法[11]以及一些组合方法[12]等。这些预测方法各有特点和适用的场合,其中卡尔曼滤波法在估计噪声的统计特性、建立卡尔曼状态方程和预测方程方面都较困难;人工神经网络方法则具有难以科学确定网络结构、学习速度慢、存在局部极小点、记忆具有不稳定性等固有缺陷;模糊逻辑法预测学习能力较弱,模糊系统的辨识还未形成完善的理论,在预测系统中选择模糊系统的结构尚需作进一步研究;空间相关性法对原始数据收集量很大,因此造成计算不方便;时间序列法建模所需信息少,运算方便,应用广泛,主要分为三种不同的模型[13]:自回归(AR)模型、滑动平均 (MA)模型和自回归—滑动平均 (ARMA)模型,时间序列法要求原始序列是平稳时间序列,但风电场功率数据往往是非线性的、非平稳性的。这就需要对非平稳和非线性时间序列处理的方法进行配合使用。
经验模式分解 (Empirical Mode Decomposition,EMD)是近几年来出现的一种用于处理非线性、非平稳信号的数据分析处理方法。相对于小波分析等信号处理方法,该方法具有自适应性,不需要去提前设定基函数,因此就能够克服依赖预测人员主观经验这一问题。另一方面,经EMD分解后能够得到有限多个基本模式分量 (Intrinsic Mode Function,IMF),尽管有些IMF可能会保持着不同程度的非平稳性,但是它们之间的相互影响作用却被隔离开来,利用这个特性可以尽可能地减小非平稳性对预测结果的影响。目前EMD已被证明在很多方面的效果皆优于其他信号处理方法[14,15]。但是,有时会出现模态混叠现象,影响分解的效果,不利于解析IMF分量的真实物理意义,降低了预测模型对各个分量的自适应性,进而影响到预测精度。集合经验模式分解 (Ensemble Empirical Mode Decomposition,EEMD)是EMD的改进方法,通过噪声辅助来对信号进行分析,减弱了模态混叠现象的影响,进而改善分析效果。
本文将EMD和EEMD方法与时间序列法相结合应用在风电场功率预测中,提出两种风功率预测方法 EMD-ARMA和 EEMD-ARMA法。首先,运用EMD和EEMD技术对原始风功率序列进行预处理,将其自适应地分解为一系列变化相对平稳的分量;其次根据各个分量的变化规律,对每一个内在模式函数进行建模并预测;最后,各分量的预测值相加即可得到最终的风电场功率预测值。
1 EMD和EEMD
1.1 EMD
经验模式分解是由N.E.Huang等人提出的一种数据分析处理方法,是一种针对非线性、非平稳信号处理的新方法。该种方法从本质上是将信号进行平稳化处理,其结果是把信号中不同尺度的波动或者趋势逐级分解开来,从而得到一系列具有不同特征尺度的数据分量,这些分量称为本征模式函数IMF(Intrinsic Mode Function)。N.E.Huang认为,对数据信号进行EMD分解时,所获得的IMF必须要满足以下2个条件[16]:
(1)对于整个时间序列来说,极值点的个数和穿过零点的个数必须要相等或者只相差1。
(2)在任意一点,其最大值和最小值包络线的平均值为0。
对于序列X(t)可以通过下述方法进行经验模式分解[17~19],其过程如图 1 所示。
(1)首先找出信号中所有局部极大值并用三次样条函数连接成上包络线,记为u(t);同理,利用三次样条插值函数连接所有局部极小值构成下包络线,记为v(t);这个上、下包络线应该包络所有的数据点。
(2)求其上、下包络线的平均值,记为m(t):m(t)=(u(t)+v(t))/2。求出原始信号与包络均值的差值:X(t)-m(t)=h(t),然后判断h(t)是否满足IMF的两个条件,若是不满足则将h(t)作为新的信号X(t),并重复以上操作,即:

一直到hk(t)满足内在模式函数的两个条件。
这样就能得到第一个IMF分量C1(t)和其信号的剩余部分r1(t)

(3)对于上面r1(t)按照步骤 (2)中的方法继续对其进行EMD分解,直到所得的剩余部分能够满足给定的终止条件,其分解过程结束。分解最终可以得到n个IMF分量及一个剩余量:

原始信号X(t)可表示为以上所有的IMF与余量之和:
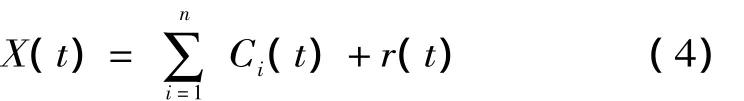
式中:r(t)为残差函数,其反映了信号的平均趋势。
N.E.Huang给出了上述过程的结束标准[20],定义了下面的标准偏差:

图1 EMD算法流程Fig.1 Flow chart of EMD algorithm

通常会将SD的取值设定在0.2到0.3之间,即:SD值满足0.2<SD<0.3时上述过程结束。此标准的物理意义为:既要使得h(t)充分接近IMF的要求,又要能控制筛分的次数,从而会使所得IMF分量保留其原始信号中的幅值调制的信息。
1.2 EEMD
由于初始信号的间断性,EMD分解会出现模态混叠现象 (即:一个IMF中包含有较宽的全异尺度的信号,或是不同的IMF分量中包含有相近尺度信号)。这样使得IMF的物理意义有所缺失,造成预测模型对信号的分量适应性下降[18],进而会影响到预测精度。为了改善模态混叠这种现象,N.E.Huang等人于2005年提出了一种新的噪声辅助数据分析的方法[19],即EEMD法。该种方法其核心思想是认为每一个观察到的数据中都融进了实际的时间序列信息和不同程度的噪声,因此,即便同一过程数据被不同的人收集得到,也应该具有不同的噪声水平,但是其整体均值将会接近于真实的时间序列。所以,为了解析出数据的实际信号,就需将多组具有有限振幅的白噪声序列加入到原始序列之上,然后分别对其进行EMD分解,之后将相应的IMF分量均值看作是真实分量。
EEMD的具体分解步骤如下:
(1)将白噪声序列添加到目标数据序列中;
(2)将添加了白噪声的信号依照上述的EMD方法分解成多个IMF;
(3)重复叠代上述步骤 (1)和 (2),但是每次需添加不同的白噪声序列;最后将分解所得到的IMF的均值作为其最终结果。
上面所添加的白噪声序列能够在时间—频率和时间—尺度空间上提供相一致的参考结构,从而能够在同一个IMF分量中比较辨识信号的不同尺度,最后可以通过对整体求平均来将白噪声序列剔除出去。因此,EEMD方法可以显著减少模态混叠现象出现的机会,进而达到有效改善EMD方法的分解效果的目的。
2 时间序列法
时间序列法是风电场短期风功率预测的主要方法之一。这种方法只需单一的风电场输出功率序列即可预测,实现起来相对比较简单。根据Box.Jenkins的方法,可以将随机时间序列分为3个模型,分别是:自回归模型 (auto regression,AR)、滑动平均模型 (moving average,MA)和自回归—滑动平均模型 (auto regression-moving average,ARMA)[21]。
由于风电场的输入风能波动很大,导致风电场输出功率数据是不平稳的,常用的预测方法ARIMA采用的是差分平稳化的方法,但其平稳化效果并不是很好,这将会直接影响预测精度。而EMD和EEMD这两种方法在对数据平稳化这方面的效果都比较好,故本文采用这两种方法来替代差分法对风电场输出功率数据进行平稳化处理。
3 改进的风电场功率预测方法
本文分别运用EMD和EEMD将原始风功率时间序列自适应分解成一系列不同尺度的IMF,将原始序列平稳化,然后通过ARMA(p,q)模型进行建模预测,最后将所有预测值累加得到最终的风电场功率预测结果,其模型结构如图2,具体预测步骤如下:
(1)利用EMD(EEMD)方法对原始风速序列进行分解得到Ci和rn。
(2)运用 ARMA(p,q)对各个 Ci和 rn分别进行建模预测。
(3)经 (2)中的预测结果相叠加即可得到风电厂出力序列的预测值。

图2 EMD-ARMA和EEMD-ARMA流程图Fig.2Flow chart of EMD-ARMA and EEMD-ARMA
在这两种预测模型中,EEMD是对EMD的改进方法,有效地减少了EMD中出现的模态混叠现象,使其分解得到的分量更加平稳,进而能够提高预测精度。但同时,EEMD分解后分量可能会更多,并且其分解所需的时间会更长,这些都将会影响预测模型的预测速度。
4 算例
本文以某风电场实测风电场功率为例,对所建模型进行验证。原始风电场功率序列为每15 min采样一个点。取其中的前470点数据用来建立模型,预测未来24个点的风功率值。
(1)EMD分解
对原始风功率时间序列进行经验模式分解。共产生7个IMF(C1~C7)和一个剩余分量r7,如图3所示。图中第1行为原始数据,这些分量展示了该功率时间序列变化的频率和振幅。同时注意到,这些分量相对于原时间序列变化较为平稳。

图3 风电场功率的EMD分解结果Fig.3 EMD results of wind power output time series
(2)EEMD分解
对上述原始风功率数据进行EEMD分解,添加100组白噪声序列到原始风电场功率序列,每组白噪声序列的标准离差均设为0.6,共产生9个IMF(C1~C7)和一个剩余分量r7,如图4所示。第1行为原始数据,其分解后的分量展示了变化的频率和振幅。同时与图3对比发现,这些分量不仅相对于原时间序列变化较为平稳,而且也比EMD分解的分量更加平稳,有效地减少模态混叠现象,从而可以提高预测精度。
(3)EMD-ARMA和EEMD-ARMA预测法
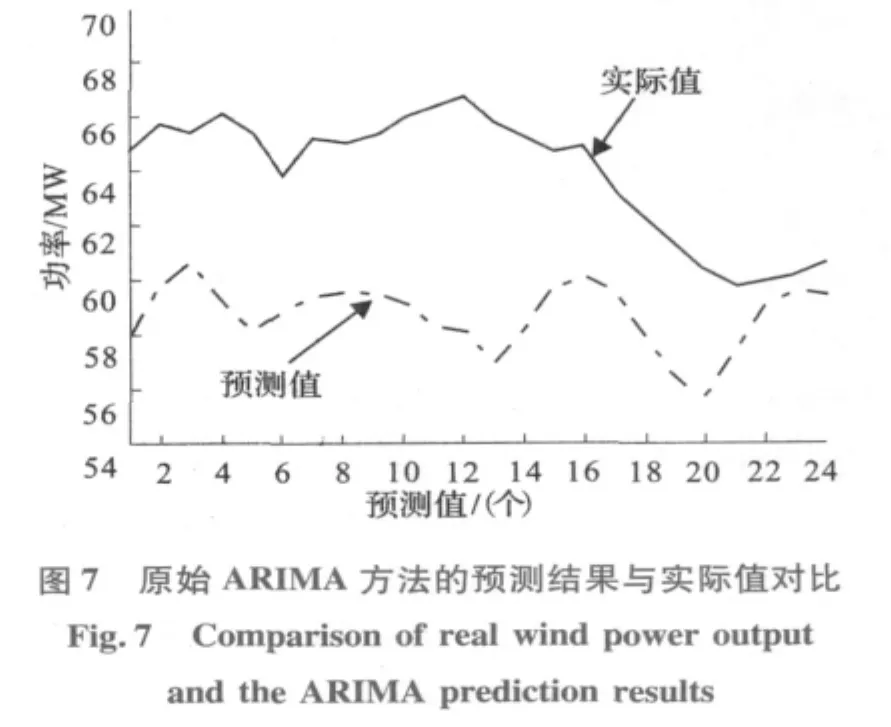
通过以上两种方法分别对原始数据进行分解,得到两组不同尺度的数据序列,然后分别对这两组数据序列的IMF分量Ci和剩余分量rn分别建立ARMA(p,q)模型并预测未来24个值,最后将所有预测值累加得到最终的风电场功率预测结果,如图5,6所示。为了进一步验证本文所提两种算法的有效性,本文又采用ARIMA模型对该风功率测试样本进行了预测,并对各种算法的预测结果进行了误差分析。图7为对原始风功率序列直接进行ARIMA建模所得的预测结果。

图4 风电场功率的EEMD分解结果Fig.4 EEMD results of wind power output time series
本文采用平均绝对百分误差 (the mean absolute percentage error,MAPE)作为误差评价指标,如公式 (6)所示。平均绝对百分误差,是用相对数形式百分数表示的预测误差指标,是衡量预测精度的重要指标。

式中:Yi表示实际风电场功率;Y^i表示风电场功率预测值;Ei表示i点预测误差;N表示预测数据的点数。
通过对预测结果的统计分析得出,采用EMDARMA方法进行风电场功率预测的平均绝对百分误差为4.21%;采用EEMD-ARMA方法进行风电场功率预测的平均绝对百分误差为1.83%;而采用ARIMA方法其平均绝对百分误差为8.03%。由图5、图6和图7所示的预测值与实际值的对比图,以及对三种方法预测结果的平均绝对百分误差进行对比后发现,相对于ARIMA而言,EMDARMA和EEMD-ARMA模型具有更高的预测精度,其中EEMD-ARMA的预测精度最高。这是因为EMD和EEMD都是将非平稳的原始风功率序列分解为一系列平稳的、具有一定规律的单一分量,跟原始风功率序列相比,这些分量更易预测,而其中EEMD的分解效果要优于EMD。EEMD分解的分量更加平稳,有效地解决了EMD中的模态混叠现象,进而提高了模型的预测精度。但是相对于EMD分解而言,EEMD分解得到的分量可能会更多,并且其分解所用时间也会更长,这就会在一定程度上影响EEMD-ARMA模型的预测速度。


5 结论
由于风电场功率序列具有非平稳性和非线性,当进行多步预测时,其预测精度难以保证。为此,本文提出了两种短期风电场功率预测方法,分别是EMD-ARMA预测法和EEMD-ARMA预测法,并以某风电场功率为例对所建预测模型进行了验证,得到如下结论。
(1)将风电场功率非平稳信号用EMD平稳化处理后,能得到一系列不同频率的平稳分量,分别对其采用时间序列法进行预测,最后通过叠加得到最终预测结果。此方法预测精度比ARIMA方法高,是一种行之有效的预测方法。
(2)在对原始风功率数据的分解上采用EEMD代替EMD,很大程度上克服了模态混叠现象,很好地保证了IMF分量具有清晰的物理意义 (即在不同的IMF分量中,给出风电场功率信号所含的不同频率成分),从而使得分解后的分量更加平稳进而得到更高的预测精度。但同时其预测速度则会比EMD-ARMA稍长一点。
[1]孙川永,彭友兵,陶树旺,等.基于神经元网络方法的风电场风电功率预报研究[J].电网与清洁能源,2011,27(12):90-94.Sun Chuanyong, Peng Youbing, Tao Shuwang, et al.Wind power Forecasting for wind farms based on neural network[J].Power System and Clean Energy,2011,27(12):90-94.
[2]孙川永,高媛媛,姜宁,等.酒泉地区风电场风电功率预报研究[J].电网与清洁能源,2011,27(7):54-57.Sun Chuanyong,Gao Yuanyuan,Jiang Ning,et al.Studies on wind power forecasting for wind farms in Jiuquan dstrict[J].Power System and Clean Energy,2011,27(7):54-57.
[3]Kariniotakis G,Mayer D,Moussafir J.Development of a next generation wind power forecasting system for the large scale integration of onshore and offshore wind farms[C].European Wind Energy Conference and Exhibition,Madrid,Spain,2003.
[4]雷亚洲,王伟胜,戴慧珠,等.风电对电力系统运行的价值分析[J].电网技术,2002,26(5):10-14.Lei Yazhou,Wang Weisheng,Dai Huizhu,et al.Analysis of wind power value to power system operation[J].Power System Technology,2002,26(5):10-14.
[5]Bossanyi E A.Short-term Wind Prediction Using Kalman Filters[J].Wind Engineering,1985,9(1):1-8.
[6]Torres J L,Garcia A,Blas M D,et al.Forecast of hourly average wind speed with ARMA models in navarre[J].Solar Energy,2005,79(1):65-77.
[7]吴国旸,肖洋,翁莎莎.风电场短期风速预测探讨[J].吉林电力,2005,(6):21-24.Wu Guoyang,Xiao Yang,Weng Shasha.Discussion about short-term forecast of wind speed on wind farm[J].Jilin E-lectric Power,2005,(6):21-24.
[8]Barbounis T G,Theocharis J B,Alexiadis M C,et al.Long-term wind speed and power forecasting using local recurrent neural network models[J].Transactions on Energy Conversion,2006,21(1):273-284.
[9]Kariniotakis G,Stavrakakis G,Nogaret E.Wind power forecasting using advanced neural network models[J].IEEE Trans on Energy Conversion,1996,11(4):762-767.
[10]Damousis I G,Dokopoulos P.A fuzzy expert system for the forecasting of wind speed and power generation in wind farms[C].22nd IEEE Power Engineering Society International Conference,2001,5(20-24):63-69.
[11]Alexiadis M,Dokopoulos P,Sahsamanoglou H,et al.Short term forecasting of wind speed and related electrical power[J].Solar Energy,1998,63(1):61-68.
[12]刘永前,韩爽,杨勇平,等.提前三小时风电机组出力组合预报研究[J].太阳能学报,2007,28(8):839-843.Liu Yongqian,Han Shuang,Yang Yongping,et al.Study on combing prediction of three hours in advance for wind power generation[J].Acta Energlae Solaris Sinica,2007,28(8):839-843.
[13]邹文,丁巧林,杨宏,等.基于Mycielski算法的风电场风速预测[J].电力科学与工程,2011,27(3):1-4.Zou Wen,Ding Qiaolin,Yang Hong,et al.Wind speed prediction based on mycielski algorithm[J].Electric Power Science and Engineering,2011,27(3):1-4
[14]杨培才,周秀骥.气候系统的非平稳行为和预测理论[J].气象学报,2005,63(5):556-570.Yang Peicai,Zhou Xiuji.On nonstationary behaviors and prediction theory of climate systems[J].Acta Meteorologica Sinica,2005,63(5):556-570.
[15]Huang N E,Shen Z,Long S,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London Series A,1998,454:903-995.
[16]Zhu Z H,Sun Y L,Ji Yu.Short-term load forecasting based on empirical mode decomposition and least square support vector machine[J].Relay,2007,35(8):38-40.
[17]栗然,王粤,肖进永.基于经验模式分解的风电场短期风速预测模型[J].中国电力,2009,42(9):77-81.Li Ran,Wang Yu,Xiao Jinyong.Short-term wind speed forecasting for wind farms based on empirical mode decomposition model[J].Electric Power,2009,42(9):77-81.
[18]刘岱,庞松岭,骆伟.基于EEMD与动态神经网络的短期负荷预测[J].东北电力大学学报 (自然科学版),2009,29(6):20-26.Liu Dai,Pang Songling,Luo Wei.Power system short-term load forecasting based on EEMD and dynamic neural network[J].Journal of Northeast Dianli University(Natural Science Edition),2009,29(6):20-26.
[19]Wu Z,Huang N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method[R].Calverton:Center for Ocean-Land-Atmosphere Studies,2005.
[20]Huang N E,Shen Z,Long S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[C].London:Proc R Soc,1998,454:903-995.
[21]蔡凯,谭伦农,李春林,等.时间序列与神经网络法相结合的短期风速预测[J].电网技术,2008,32(8):82-85.Cai Kai,Tan Lunnong,Li Chunlin,et al.Short-term wind speed forecasting combing time series and neural network method[J].Power System Technology,2008,32(8):82-85.
