雷达干扰训练器噪声干扰源的设计
2012-09-19邹向阳胡巍彪
王 琪 邹向阳 胡巍彪
(桂林电子科技大学电子工程与自动化学院1,广西 桂林 541004;桂林空军学院警卫指挥系2,广西 桂林 541003)
0 引言
随着数字电子技术的发展,数字噪声发生器越来越受到人们的重视。数字随机噪声通过随机数表达,由于控制器和存储器的精度有限,现有的随机数产生算法均为伪随机数产生算法[1-2]。近年来,混沌序列越来越受到重视,其具有非线性、遍历性、初值敏感性、类噪声性等特点[3],可以实现噪声遮蔽式干扰的目的。因此,混沌序列在电子对抗领域有很大的发展空间。同时,直接数字频率合成(direct digital synthesizer,DDS)技术也越来越成熟,精度也越来越高,在雷达噪声瞄准方面也有用武之地。
1 系统设计方案
基于混沌伪随机数叠加DDS数字信号的高精度数字式噪声发生器原理如图1所示。
在FPGA中,首先采用VHDL语言结合原理图产生混沌序列,通过高斯映射法将其映射为高斯分布的伪随机噪声,同时在FPGA中完成DDS算法;然后,通过查表,产生DDS高精度数字序列,并与伪随机数字噪声进行叠加合成,得到复杂噪声序列;最后,将得到的数字序列分别通过高速D/A转换器、低通滤波器和运算放大器转换为所需要的某型号雷达噪声干扰信号。
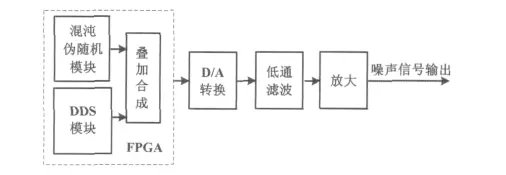
图1 基于FPGA的数字噪声发生器原理图Fig.1 Principle of the digital noise generator based on FPGA
2 混沌伪随机模块
2.1 混沌伪随机序列的分析
混沌是自然界中非线性确定系统的一种内在随机过程的表现[4]。混沌系统对初始条件及其参数很敏感,它能够产生大量非相关的、类噪声、可再生的混沌信号,而且它们具有宽谱特征,在时域上存在类似噪声的随机行为,从而弥补了传统伪码序列数量少的缺憾。
改进型Logistic映射的递推公式[5]、概率密度函数分别为:

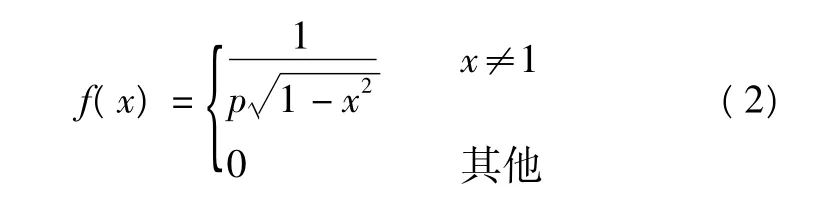
由改进型Logistic混沌映射得到的混沌序列服从同一分布,且该序列对初始条件特别敏感。两个不同初值的混沌系统,经过相同迭代次数得到的两个序列,可以认为是相互独立的,其互相关函数为0。
自相关函数:

互相关函数:
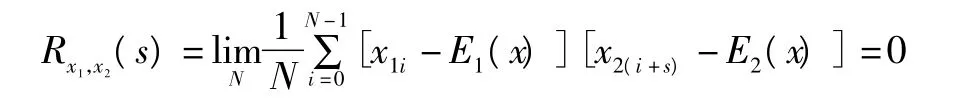
由此可知,改进型Logistic映射产生的混沌序列均值为0。该序列具有理想自相关和互不相关特性,非常适合用作数字随机噪声模型。
2.2 混沌伪随机序列的转换
通过映射函数法,将混沌伪随机序列的均匀白噪声快速转化为高斯白噪声,具体算法如下。
设X服从均匀分布,Y服从高斯分布且其概率密度函数为f(y)。首先将随机变量Y进行均匀离散化,得到离散序列{yi|i=1,2,…,N},取各离散点的概率为Pi,对应的函数值为f(yi),将每个f(yi)映射到均匀分布的随机变量 X的某一区间上[xi,xi+1],满足‖xi+1-xi‖=f(yi),也就是xi落入与 Pi对应的区间时,即实现了均匀分布随机变量X到高斯分布随机变量Y之间的映射函数关系。这样就可以得到一个映射表。根据映射函数曲线建立均匀分布到高斯分布的映射表,以均匀随机数为地址查找映射表,可得到高斯分布白噪声,实现了混沌伪随机序列转化。
混沌映射法产生的伪随机噪声理论上周期应该为无限长,但在实际计算中,存在有限精度效应、硬件位数的限制和运算速度的要求。因此,混沌序列在迭代过程中必须退化为周期序列,精度越高、周期越长。当精度达到32位时,序列已经很好地满足了要求。为了获得周期足够长的序列,可用不同的初始值分别对Logistic映射进行迭代。
3 DDS模块
3.1 DDS 原理
随着数字集成电路和微电子技术的发展,直接数字频率合成(DDS)技术逐渐体现出其相对带宽宽、频率转换时间短、频率分辨率高、输出相位连续、可编程及全数字化结构等优点[6]。
DDS原理框图如图2所示,它包含相位累加器、波形存储器、数模转换器、低通滤波器和参考频率源五部分[7]。
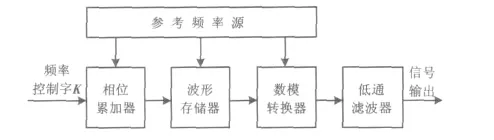
图2 DDS原理框图Fig.2 Principle of DDS

3.2 DDS累加器的设计
累加器是DDS设计的核心,它决定了DDS的精度[8]。为了提高运算速度和精度,对累加器的设计采用了流水线技术,即把一个位数很长的加法拆分成N个位数较短的加法,在N个时钟周期内完成运算[9](N为流水线的级数)。采用流水线结构以后,加法器的字长变短。
对于FPGA来说,加法器字长变短对工作频率的提高非常有效。当然,流水线结构的使用并不能无限制地提高电路的工作速度。随着流水线级数的提高,电路会变得非常的复杂,当电路的复杂度达到一定程度时,将造成工作性能的下降。这样流水线结构就不再具有提高电路工作频率的作用,运算速度也没有提升。本系统采用了八级流水线结构,明显提高了运算速度和精度,达到了系统要求。
3.3 ROM表的优化处理
ROM表的采样点数决定了输出信号的精度[10],但如果ROM表太大,就会占用设计中大量有限的硬件资源。设计中利用标准对称性,对 ROM表进行了优化处理,具体方法如下。
简单来说,DDS根据奈奎斯特采样定理,从连续信号的相位出发,对一个正弦信号进行采样、量化、编码,最后形成一个正弦函数表,并存储在查询表ROM中。当每一个参考时钟脉冲fc输入时,相位累加器进行计数,相位的增量值由频率控制字K决定。累加器产生线性增加的阶梯信号,然后对ROM寻址,最后将寻址得到的波形数据值,经过转换处理后,得到正弦波信号。
DDS输出信号的频率与时钟频率fc以及频率控制字K、累加器位数N之间的关系为:
存放在ROM中的波形数据并不是一个完整的周期,而是只存放1/4个周期的波形。以正弦波为例,因为正弦波的正半周和负半周正好相反,而第一象限和第二象限幅度对应相同,第三象限和第四象限波形对应幅度也相同,所以只需利用[0,p/2]上的采样点,便可模拟出整个[0,2p]的正弦函数。
存储数据必须含有象限信息,而相位码的前两位就是象限信息:①“00”为第Ⅰ象限;②“01”为第Ⅱ象限;③“10”为第Ⅲ象限;④“11”为第Ⅳ象限。相位码的第一位包含了正负极性标志,“0”为正极性,“1”为负极性。
4 硬件选择与分析
FPGA采用Cyclone II EP2C8Q208芯片。其等效门数为42万门,内嵌乘法器时钟采用50 MHz有源晶振,通过EP2C8内部锁相回路(phase locked loop,PLL),将50 MHz三倍频到150 MHz作为系统全局时钟。混沌伪随机模块、DDS模块叠加合成在FPGA内完成。
为了提高量化精度,必须增加D/A转换的位数。同时,为了提高带宽和转换速率,必须加快D/A转换的采样速率,所以本文选用 Analog Device公司的AD9752D/A作为D/A器件。该芯片是单电源供电的低功耗电流输出型的12位并行高速数模转换器,支持速率高达125 MS/s,建立时间不大于35 ns,能够满足系统对D/A的要求。
5 结束语
系统设计完成后,根据设计要求,分别对系统混沌噪声信号、DDS信号、DDS叠加噪声信号以及幅度调节等功能进行了测试。试验结果表明,波形显示正常,无明显失真,输出幅值误差在1%以内。
测试结果表明,该噪声发生器产生的复杂数字噪声对雷达具有很好的干扰作用。
[1]陈邦媛.射频通信电路[M].北京:科学出版社,2002.
[2]张瑞华,刘庆华,周德新.伪随机噪声产生算法及DSP实现[J].声学与电子工程,2003,70(2):22 -45.
[3]罗松江,丘水生,陈旭.一种混沌伪随机序列复杂度分析方法[J].华南理工大学学报:自然科学版,2010,38(1):18 -20.
[4]冯海涛.混沌随机数发生器的设计与应用[D].成都:西南交通大学,2006.
[5]刘建夏.一种混沌伪随机序列的设计及其应用[J].计算机工程,2005,31(18):150 -152.
[6]霍志勇.基于DDS的雷达扫频信号产生系统研究[D].西安:西安电子科技大学,2005.
[7]周红艳.一种基于 DDS的函数发生器[J].机电工程,2011,28(1):83 -86.
[8]向道朴.宽带步进频率雷达信号源的设计与实现[D].长沙:国防科技大学,2006.
[9]王元华.基于DDS技术的虚拟式任意波形发生器研究[D].济南:山东大学,2007.
[10]任建新,余乐永,张鹏.基于FPGA的高精度信号发生器的实现与优化[J].测控技术,2011,30(1):13-16.
