爆破振动信号的HHT时频能量谱分析＊

关晓磊，颜景龙

（1.中北大学电子测试技术国家重点实验室，山西 太原 030051；2.北京理工大学机电学院，北京 100081）

随着信号分析技术的发展，对爆破的了解已不止于时域和频域的独立分析，短时傅立叶变换和小波变换在一定程度上可对信号进行时频分析，但都基于傅立叶变换，要求被分析信号必须平稳。爆破振动信号是典型的非平稳随机信号，严格意义上基于傅立叶变换的分析方法不具有适用性［1］。希尔伯特－黄变换（Hilbert－Huang transform，HHT）是近几年兴起的非平稳随机信号分析新方法［2－3］，它对信号进行平稳化处理，即将信号经过经验模态分解（empirical mode decomposition，EMD），产生一系列具有不同特征尺度的固有模态函数（intrinsic mode function，IMF），然后计算IMF信号的瞬时属性。用时频域联合能量法分析振动信号，能够较好反映振动强度、频谱特征，特别是持续时间对建筑物的影响，比现行的独立域参数更科学。

1 爆破振动信号HHT分析

爆破振动信号HHT分析的步骤如图1所示。

图1 HHT分析步骤Fig.1 The HHT analysis steps

1.1 EMD分解

为了研究瞬态和非平稳现象，频率必须是时间的函数。非平稳随机信号通过EMD过程后，得到一系列IMF分量，而IMF使瞬时频率具有意义。针对爆破振动信号的信号特征，在HHT中对EMD端点效应、拟合的欠包络现象、筛选终止准则等问题进行了改进。

1.1.1 首尾极值点对称延拓

对于原始信号X（t），先要找出所有极值点进行上下包络的拟合。由于数据首尾段数据缺少极值点，拟合时就会造成端点飞翼现象。爆破振动信号属于低频信号，极值点之间的时间跨度大，端部的端点效应容易影响信号内部［4］。通常在数据两端加入特征波抑制端点效应。微差爆破（毫秒延期爆破）能够很好地实现降震，所以现有工程爆破多为微差爆破，这使得爆破振动的首尾极值点两侧数据多具有对称特点。利用这个特性进行对称延拓，消除爆破振动信号HHT变换的端点效应。

步骤如下：计算端点处首个极值点x（m）（m为x（n）首个极值点索引位置，x（n）为X（t）的采样值）两侧数据对称度ξ。若ξ在规定阈值内，则以该极值点为对称轴对称4～5个极值点；若首尾极值点两侧数据对称性较差，则采用镜像法［4－5］。定义对称度为

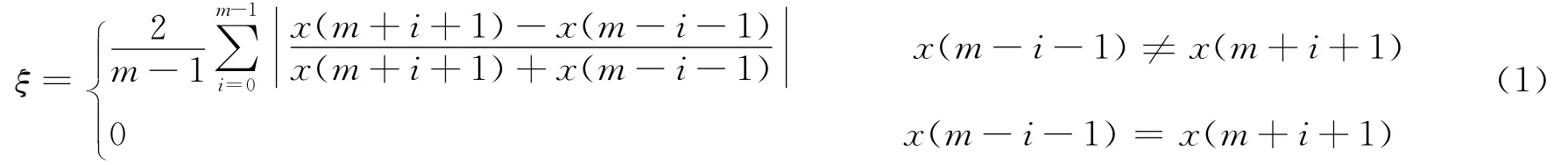
一般取ξ参考门限为0.1～0.2（实际ξ越大，说明对称性越差），即：实际ξ低于门限，则采用首尾极值点作为对称轴对称延拓一定数量极值点数据；若ξ大于门限，说明对称性差，则采用端点镜像对称延拓。

图2为实测数据和首极值点对称向前延拓后的曲线，对称延拓后曲线仍保持平滑。延拓后进行曲线的上下包络拟合，得到合格的IMF后截取原始数据对应的数据。

图2 原始曲线和首极值点对称延拓后曲线Fig.2 The original curve and the curve after extension

1.1.2 插值算法

图3 三次样条插值与分段三次Hemite保形插值Fig.3 The cubic spline interpolation and the Hermite interpolation of picecwise cubic

传统的EMD插值算法采用三次样条插值，但是容易出现欠包络现象，即上下包络线局部无法完整包裹当前信号。于是，采用了分段三次Hemite保形插值算法。它与三次样条插值算法的不同之处在于计算插值点处一阶导数的方法不同。保形插值计算插值点xk一阶导数dk的方法更简单、直接，即：当δk和δk－1同号时，（w1＋w2）／dk＝w1／δk－1＋w2／δk，其中δk是子区间xk≤x≤xk＋1的折线斜率，w1＝2hk＋hk－1，w2＝hk＋2hk－1（hk＝xk＋1－xk，即区间步长）；当δk和δk－1异号时，dk＝0。

由图3可以看出，分段三次Hemite保形插值较好地保留了原始曲线的形状，而三次样条插值的效果欠佳，在300和320ms时刻的包络发生形状变化，出现过包络。

1.1.3 筛分终止准则

拟合得到上下包络线Xmax（t）和Xmin（t）后，能够得到一条均值线，然后得到h1（t）

需要对h1（t）进行判断，判断h1（t）是否为合格的IMF分量，若不是则将h1（t）作为原信号X（t）重复上述步骤，直到得到合格的h1k（t），即IMF0。一般地，采用基于整体数据标准差σs必然忽略了数据的局部特性，所以出现了基于局部的终止条件。设局部均值线为q（t）＝［Xmax（t）－Xmin（t）］／2，幅值函数为a（t）＝［Xmax（t）＋Xmin（t）］／2，定义函数

将σ（t）作为判定筛选终止的判据，设定门限值θ1、θ2和α，规定当σ（t）中数据小于θ1的比例达到α、且不存在大于θ2的数据时，终止筛选。一般默认θ1＝0.05，θ2＝0.5，α＝0.95。与标准差σs相比，σ（t）更能反映IMF的均值特性，且两个条件相互补充，使信号只能在局部出现较大波动，保证整体均值为零［6］。为防止筛分发散和误差累积，一般对筛分次数做限制。

图4中，h1（t）频率范围较宽，经过不断筛选得到频率较为单一的h121（t），即IMF，且h在各个时间段上都具有较好的频率一致性，说明局部终止准则得到的IMF局部特性较好。

1.1.4 模态分解终止条件

EMD分解得到一个IMF后，用原信号减去IMF便是信号残差，若残差为单调函数或整体均值小于预定误差则完成了EMD。

图5为信号分解得到的IMF及其频谱。由图5可以看出，从IFM0～IFM7频率逐渐降低，说明了EMD具有自适应性，且主要分布在50Hz以下，到最后几乎成为一条直线；IMF0频带较宽，含有较多的高频量，说明含有高频噪声；IMF1～IMF3的幅度比其他分量高，说明振动有用信号主要分布在这些分量中。

1.2 瞬时属性估计的改进算法

采用Hilbert变换法计算瞬时频率，很容易出现无意义的负频率，而基于经验的AM－FM分解可以很好地解决这个问题。过程中，把IMF唯一地分成包络部分AM和载波部分FM［7］。其中，FM可直接计算正交项DQ，且FM是单位振幅，满足了Bedrosian定理的要求；同时，标准化的FM可以给出更加局部化、更加实用的基于能量的误差。

1.2.1 AM－FM 分解

标准化的过程基于经验的、通过拟合数据的多次迭代实现。首先，找到IMF数据xi（t）绝对值的所有局部极大值点，然后利用曲线拟合所有极大值点，得到包络e1（t）；同样在过程中，使用极值点对称延拓法补充极值点，然后进行标准化处理

由于拟合仅穿过极大值点，在振幅快速变化的地方包络样条可能会穿到数据点之下，所以IMF一般大于单位振幅。为了得到单位振幅的FM，采用迭代法对y1（t）再进行标准化

经过n次迭代后，yn（t）的所有值都等于或者小于1，标准化就结束了。这时，得到FM部分Fi（t），同时得到包络AM部分Ai（t），也即调频部分，作为瞬时振幅。这种方法绕开了Bedrosian条件的限制，对于波形局部零均值且对称的IMF信号，能够有效计算瞬时振幅

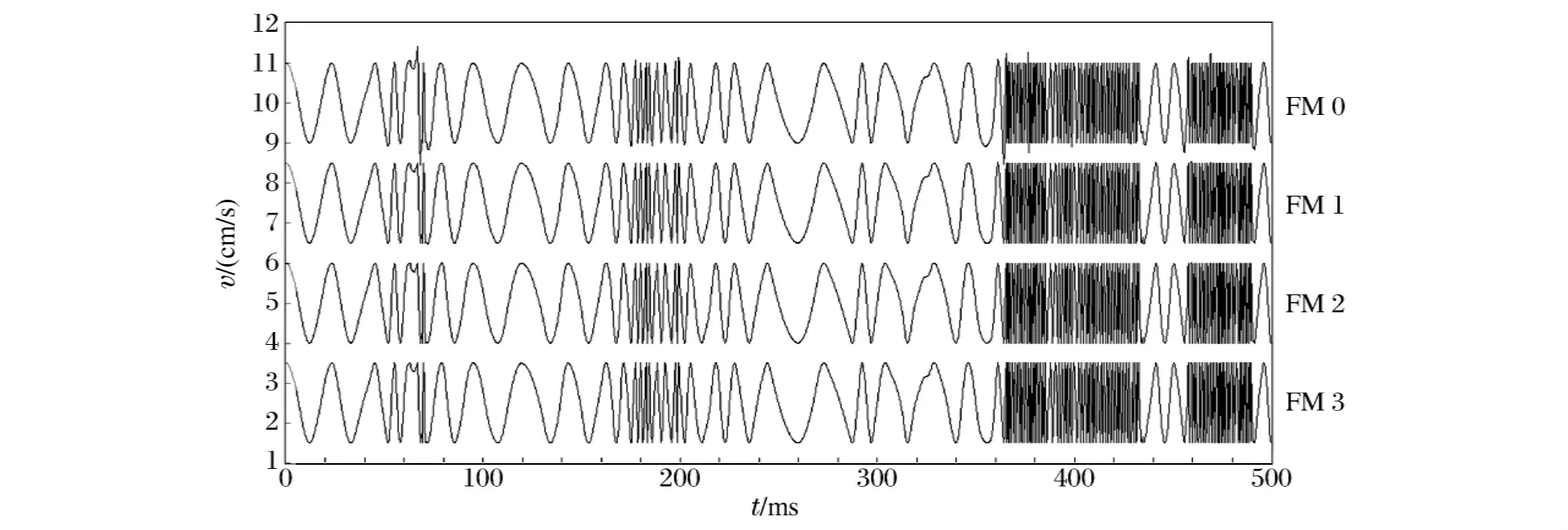
图6 迭代算法的过程Fig.6 The process of the iterative algorithm

由图6可以看出，FM0曲线存在幅度大于1的数据段，一次迭代后FM1接近单位振幅，最后FM2完全为单位振幅，即IMF0的FM部分F0（t），然后通过计算得到AM部分。通过对FM部分进行计算得到正交项，进而计算相位角，最后得到瞬时频率。

1.2.2 瞬时频率计算

基于经验的AM－FM分解得到了IMF信号的正交项，跳过了采用希尔伯特变换计算瞬时频率的过程。标准化之后得到FM部分为信号载波部分F（t），得正交项为

它最大的优点是没有使用希尔伯特变换，不涉及积分过程，不受临近点的影响，且瞬时频率通过求导运算得到，所以局部性很好。于是，相位角和瞬时频率为

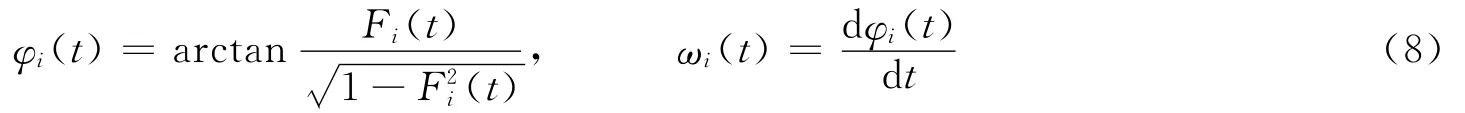
式中反正切和反余弦理论上是等价的，但计算方法不一样，反正切的计算稳定性较高。

由图7可以看出，所有IMF分量的瞬时频率主要集中在60Hz以下，60Hz以上的为IMF0的部分时刻，说明高频噪声主要集中在IMF0中。

图7 瞬时频率Fig.7 Instantaneous frequencies

2 能量计算

HHT的定义为

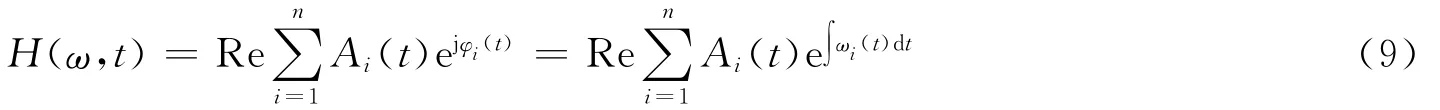
式中：瞬时频率为各IMF经过AM－FM分解后的FM部分经过直接正交计算所得的ωi（t），H（ω，t）为相应IMF的AM部分Ai（t）幅值。三维时频能量谱为H2（ω，t）随时间和瞬时频率的分布。

瞬时能量

式（10）反映了信号能量随时间变化的情况，对于爆破，它代表了雷管爆炸造成的振动能量的激发，可参照谱图和起爆时序估计雷管是否起爆［8］。

以某矿爆破实测信号（竖直方向）为例，爆破振动信号判据主要用最大振速、主频和持续时间三个独立参数对信号进行衡量。采样频率5kHz，最大振速6.858cm／s，持续时间约400ms，FFT频域主频38Hz。从瞬时能量图和实际数码电子雷管爆破时序对比（见图8）可见，每个尖峰是雷管爆炸产生的能量激发，能量在120和270ms时刻附近较高，说明这些时间内的爆破振动的能量较大，也即爆炸的能量较大，雷管的装药量较大。

三维时频能量谱如图9所示。HHT时频能量谱能够直观地从时域（持续时间）和频域（主振频带）角度反映爆破振动信号的能量分布。相对于单纯的时域分析，HHT能够表明任意频段和幅值范围的振动的持续时间；相对于FFT分析，HHT能够表明任意时间段和范围的振动能量的频率分布。如图9所示，能量主要集中在10～60Hz，时间主要集中在120和270ms左右，能量集中范围中心频率40Hz左右。按照GB6722－2004《爆破安全规程》，建筑物的允许频率在10Hz以内，因此爆破不会对建筑物构成影响。

图8 原始数据曲线和瞬时能量谱Fig.8 The original data curves and the instantaneous energy spectrum

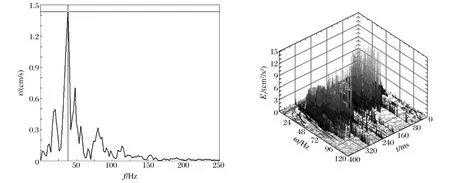
图9 FFT幅度谱和三维时频能量谱Fig.9 The FFT amplitude spectrum and the three－dimensional spectrum of time－frequency power

3 结 论

采用HHT变换可以对爆破振动信号进行更加科学的分析。对于爆破振动信号，按照信号特征采用了首尾极值点对称法对信号进行延拓，较好地抑制了端点效应；采用分段三次Hemite保形插值对极值点进行拟合，比三次样条插值拟合更能保留信号的原始外形；局部的终止准则能够较好地保留信号的局部特征，但会出现筛分次数较多、筛分发散的问题；采用AM－FM分解计算IMF瞬时属性，比Hilbert变换更准确，并且不会出现负频率现象。最后，HHT时频能量谱由时频角度分析振动信号能量分布，可更好地参照爆破安全规程就爆破振动对建筑物是否有影响作出判断。

［1］张义平.爆破震动信号的HHT分析和应用研究［D］.武汉：中南大学，2006.

［2］Huang N E，WU Zhao－hua，Long S R，et al.On instantaneous frequency［J］.Advances in Adaptive Data Analysis，2009，1（2）：177－229.

［3］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition method and the Hilbert spectrum for nonstationary time series analysis［J］.Proceedings of the Royal Society of London：A，1998，454：903－995.

［4］张进林.抑制经验模态分解端点效应的常用方法性能比较研究［D］.昆明：云南大学，2010.

［5］WU Fang－ji，QU Liang－sheng.An improved method for restraining the end effect in empirical mode decomposition and its applications to the fault diagnosis of large rotating machinery［J］.Journal of Sound and Vibration，2008，314（3）：586－602.

［6］Niazy R K，Beckmann C F，Brady J M，et al.Performance evaluation of ensemble empirical mode decomposition［J］.Advances in Adaptive Data Analysis，2009，1（2）：231－242.

［7］王国栋.信号瞬时频率的估算［D］.广州：中山大学，2010.

［8］陈银鲁.爆破振动信号的能量分析方法及其应用研究［D］.杭州：浙江大学，2010.