冲击波作用下LY12铝合金结构毁伤的数值模拟＊

侯日立，周 平，彭建祥

（1.空军第一航空学院，河南 信阳 464000；2.中国工程物理研究院流体物理研究所，四川 绵阳 621900）

导弹或高能射弹战斗部爆炸时产生的冲击波是飞机面临的基本威胁之一，研究它对目标结构的毁伤判据，对飞机生存力分析、战伤抢修中的损伤预估以及武器效能评估都具有非常重要的意义。工程应用中，最常用的估算方法是以有效作用距离为判据的平方根关系［1－2］，即

式中：D为有效作用距离，单位为m；W 为装药质量，单位为kg；K为经验参数，根据空中目标类型的不同取值在0.3～0.5。当目标离爆炸源的距离小于D时，认为目标完全破坏。这一判据实际上以临界超压计算为依据，但相同质量的炸药在离海平面不同的高度爆炸，产生的超压有很大区别。以装药量2.71kg、超压临界破坏值100kPa为例，在海平面对应的临界距离为7.99m，在5和10km高空，对应的临界距离则分别为5.01和2.71m。可见，有效距离估算法具有很大的局限性。除此之外，现有关于爆炸冲击波对目标的毁伤准则主要有［3－5］：超压准则、冲量准则以及超压－冲量准则（p－I准则）。这些准则的共同点是考虑了冲击波威力场的三个基本参数（超压、正压作用时间和比冲量，其中只有两个参数是独立的），但忽略了目标自身抵抗破坏的能力。事实上，目标各部件有各自不同的强度、刚度和自然响应频率，对冲击波作用下的毁伤有不同的抵抗能力［6］。冲击波作用下结构毁伤判据问题涉及的影响因素多、关系复杂，纯粹用实验方法研究不仅费用高、周期长，而且不容易把各因素的作用有效地分离。

本文中，利用LS－DYNA有限元动力分析软件，以飞机结构常用的LY12铝合金平板结构为对象，通过正交实验设计，用数值模拟研究爆炸冲击波的超压、正压作用时间，材料屈服强度以及结构的自然响应频率等多个因素对结构破坏的影响规律，提出一个以临界超压为函数、爆炸冲击波正压作用时间以及材料屈服强度、结构自振频率为参数的破坏判据，并与文献［7］实验结果比较。

图1 计算模型Fig.1 Calculation model

1 计算方案及模型

选择与文献［7］实验方案相同的材料和几何尺寸，即400mm×500mm的LY12铝合金板。靶板厚度分别取1、2、3、4、5mm。文献［7］的实验中，靶板用14个M10的螺钉和压板固定在框架上。模拟计算中，为了既能考虑螺钉孔处的应力集中以及螺钉孔对结构承载能力的削弱作用，又能避免分析螺钉与板孔复杂的接触问题，采取了对实验件四周侧面进行约束的简化措施，如图1所示。

数值模拟中采用有限元动力分析软件LS－DYNA，单元类型为shell 163壳单元。爆炸冲击波采用三角形脉冲模拟，垂直作用在整个靶板上。针对上述五种不同厚度的结构，在不同的正压作用时间、材料强度下计算临界超压。其中，临界超压定义为结构中开始出现单元失效时对应的超压。由于涉及多种实验条件，本文中采用正交方法进行实验设计。材料模型选用Johnson－Cook本构关系［8］（JC模型）

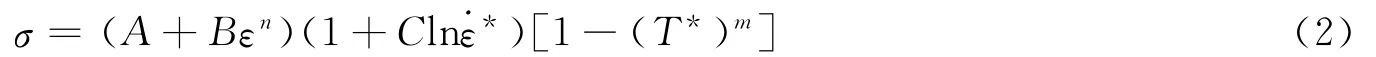
式中：Δε为加载过程中的等效塑性应变增量，σ＊为平均应力与等效应力的比值，D1、D2、D3、D4、D5为常数。当D达到1.0时，材料失效。

LY12铝合金的相关模型参数分别为［9－10］：A＝369MPa，B＝684MPa，C＝0.008 3，n＝0.73，m＝1.7，D1＝0.13，D2＝0.13，D3＝－1.5，D4＝0.011，D5＝0，ρ＝2.8g／cm3，E＝68GPa，μ＝0.33。

2 数值模拟结果及分析

不同条件下正交实验结果如表1所示。表中结构自振频率利用结构分析软件通过模态分析获得。

计算表明，所有模拟实验都是从螺孔处开始破坏，如图2所示，这与实验情况是完全符合的。

表1 计算结果Table1 Calculation results

图2 数值模拟结果Fig.2 Results of numerical simulation

处理后得到的各变量对临界超压的影响规律如图3～5所示。为了选择合适的函数关系，在更宽的范围表征相应的变化规律，本文中作了如下考虑。（1）关于正压作用时间对临界超压的影响。从图3可以看出，随着正压时间的缩短，临界超压是单调快速增加的，但从材料破坏机理看，这种增加显然是有界的，因为超压值不能超过材料的剪切强度。另外，随着正压作用时间的增加，临界超压下降的趋势很快趋缓，如果正压作用时间无限增大，则应趋向于静压作用的情况，亦即临界超压值不能低于相应的静压破坏压力。基于上述考虑，结合图3，Δpc－t＋关系拟选用指数函数描述。（2）关于结构自振频率对临界超压的影响。对于薄板结构，在材料的弹性模量、密度、泊松比确定的情况下，自振频率主要决定于板材的厚度。显然，厚度越小越容易破坏，反之亦然，结合图4，Δpc－f关系拟选用线性函数Δpc＝m4f描述。（3）关于材料强度对临界超压的影响，需要考虑材料的破坏准则。从式（4）含σ的作用项可以看出，σ对临界破坏条件的影响是指数变化关系，结合图5，Δpc－σ关系拟选用指数函数描述。

图3 不同正压作用时间下的临界超压Fig.3 Critical overpressure under different positive phase duration

图4 结构自振频率对临界超压的影响Fig.4 Critical overpressure vs.natural vibration frequency

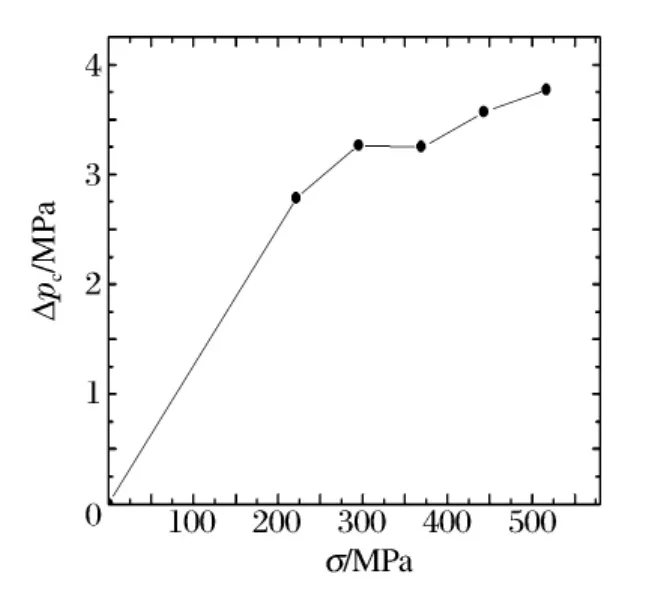
图5 材料强度对临界超压的影响Fig.5 Critical overpressure vs.yield strength

以上是单一因素对临界超压影响规律的分析，而实际情况中，三个因素同时起作用。就像JC模型中的应变、应变率、温度等三个因素对流动应力的影响一样。参照JC模型的建模思路，综合考虑正压作用时间、材料强度、结构自振频率的影响后，构建临界超压计算公式

模型中四个参数A、B、C、D的确定方法如下：先将等号右边中三个变量中的两个固定，然后进行实验（本文中采用的是数值模拟实验，实验结果见表2中的No.26～39），最后对实验结果分别拟合，确定相关模型参数。具体步骤如下：第一步，取σ＝369MPa、f＝89.3Hz，改变t＋，得到一组数据，如图6所示，拟合后得到C＝485.3。第二步，取t＋＝1000μs、f＝89.3Hz，改变σ，得到一组数据，如图7所示，拟合后得到D＝48.1。第三步，利用拟合得到的D，回到第一步，可得到A＝0.018 4。第四步，取σ＝369MPa，t＋＝1000μs，改变f，得到一组数据，如图8所示，拟合后得到B＝2.82。代入所有参数后，得到铝合金平板结构的损伤判据

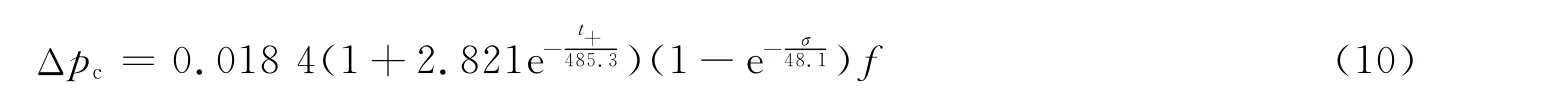
式中：Δpc、t＋、σ和f 的单位分别为 MPa、μs、MPa和 Hz。

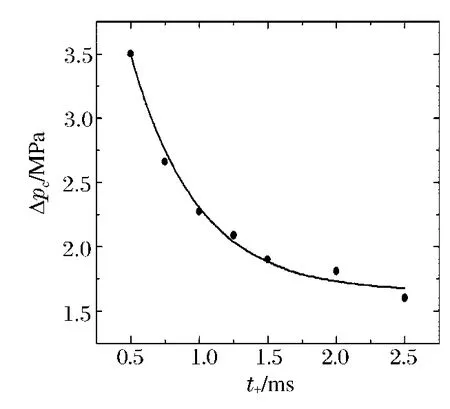
图6 超压－时间关系的参数拟合Fig.6 Parameters fitting between critical overpressure and positive phase duration

图7 超压－强度关系的参数拟合Fig.7 Parameters fitting between critical overpressure and strength

图8 超压－自振频率关系的参数拟合Fig.8 Parameters fitting between critical overpressure and natural vibration frequency

3 与实验结果的比较

为了验证数值模拟方法以及得到的损伤判据的合理性，与实验结果进行比较。冯顺山等［7］通过在爆炸筒内的实验，获得了不同厚度LY12硬铝板在冲击波作用下发生破坏的临界距离（见表2）。一般认为［1］，当炸药离开地面的距离满足条件时，即认为在无限空域中爆炸，可用以下公式计算超压和正压作用时间

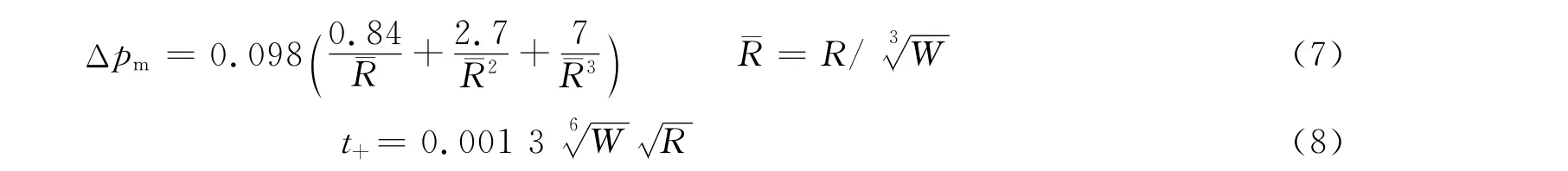
式中：R为目标离爆炸点的距离，单位为 m；W 为炸药的TNT当量，单位为kg；t＋的单位为s。本文中利用以上公式对文献［7］中各临界位置处的超压、正压作用时间、自振频率进行了计算，并与本文预测模型得到的临界超压进行了比较，如表2所示。表中，h为靶板厚度，l为实测断裂长度，N为实测螺钉孔拉断个数。可以看出，二者基本吻合。

表2 冲击波破坏实验及与理论判据的比较Table2 Comparison between theoretical calculation and experimental results

4 结 论

爆炸冲击波作用下，目标结构的损伤既与冲击波威力场有关，又与目标自身结构参数有关，还与二者的交会条件有关。以冲击波临界超压为函数，以正压作用时间、目标材料的极限强度以及自振频率等为变量建立的损伤判据，综合了冲击波威力场以及目标自身结构参数的影响，实验表明，对目标的临界损伤具有较好的描述能力。当然，本文中只是讨论了冲击波垂直作用于平板结构靶板的损伤问题，实际目标往往还有加强筋等复杂结构，而且冲击波与目标的交会角度也往往具有任意性，这些问题需要在下一步工作中继续深入研究。

［1］张志鸿，周申生.防空导弹引信与战斗部配合效率和战斗部设计［M］.北京：宇航出版社，1994.

［2］隋树元，王树山.终点效应学［M］.北京：国防工业出版社，2000.

［3］北京工业学院八系.爆炸及其作用（下册）［M］.北京：国防工业出版社，1979.

［4］Abrahamson G R，Lindberg H E.Peak load－impulse characterization of critical pulse loads in structural dynamics，in dynamic response of structure［M］.New York：Permagan Press，1972.

［5］钟倩.爆炸源毁伤效应评测方法研究［D］.南京：南京理工大学，2007.

［6］Haverdings W.General description of the missile systems damage assessment code（MISDAC）［R］.ADA 288622，1994.

［7］冯顺山，蒋浩征.小药量爆炸冲击波对飞机毁伤效应的研究［J］.兵工学报：弹箭分册，1987，1：17－25.FENG Shun－shan，JIANG Hao－zheng.Research on destroy effect of aircraft by blast shockwave of small charge［J］.Projectile and Rocket Fascicule of Acta Armamentarii，1987，1：17－25.

［8］Johnson G R，Cook H.A constitutive model and data for metals subjected to large strains，high rates and high temperatures［C］∥Proceedings of the Seventh International Symposium on Ballistics.The Hague，The Netherland，1983：541－547.

［9］Lesuer D R.Experimental investigation of materials models for Ti－6Al－4Vtitanium and 2024－T3aluminum［R］.Washington：Office of Aviation Research，2000.

［10］《工程材料实用手册》编辑委员会.工程材料实用手册（第3卷）［M］.北京：中国标准出版社，2002.