关于高等数学教学的几点认识
2012-09-18沈菁华
沈菁华
关于高等数学教学的几点认识
沈菁华
摘 要:为了提高高等数学课程的课堂教学质量,深化高等数学教学改革,本文从作者的教学实践出发,就如何改革高等数学的教学方法和提高学生的学习兴趣提出了一些见解:注重数学思想方法传授,启迪学生的创新思维;融入数学史、数学文化的内容;强调实际应用;注重几何直观的引入。
关键词:高等数学;创新思维;数学史
沈菁华/苏州科技学院数理学院讲师(江苏苏州215009)。
在高等教育课程体系中,高等数学是很多专业必修且最重要的基础课程之一,也是培养学生能力和提高学生素质的一门重要学科。它不但为学生学习后续课程提供必要的数学知识和方法,同时也是培养学生运用数学理论和方法分析和解决问题的能力、培养逻辑思维能力和空间想象力的重要途径。但是,学生学习的现状却不容乐观,学生在学习掌握这门课的过程中普遍感到概念抽象,思维难于展开,面对问题难于入手,方法难于掌握。如何激发学生的兴趣、提高高等数学的教学质量,已经成为我们迫切需要解决的问题。针对这一现象,在教学过程中,要充分体现以人为本的教学理念;要求教师必须认真钻研教材,突出高等数学的实用性和趣味性,并能及时调整教学案例,综合应用多种教学手段授课。以下,笔者根据多年的教学实践,谈谈对高等数学教学的几点认识。
一、注重数学思想方法传授,启迪学生的创新思维

在这一过程中,将新内容和学生已经熟悉的知识进行类比,使学生更容易理解、接受,有利于新知识的掌握,教学取得了良好的效果,同时也培养了学生的创新思维。
二、融入数学史、数学文化的内容
任何知识都是产生在一定的历史背景中,所以,在开始讲授高数课程之前,我们都会将微积分的发展史利用一节课的时间作一简单介绍。从公元前5世纪极限思想的萌芽,到古希腊的阿基米德所建立的确定面积和体积的方法,到牛顿、莱布尼茨建立微积分,再到微积分理论基础的完善。微积分的发现历经2000多年的历程,可以说是人类历史上的奇迹,而学生们虽然高中学过导数和微分,有的甚至知道积分的计算方法,但是他们对于微积分的发展历史却几乎一无所知,这不能不说是中学教育的失败。通过对微积分历史的简单回顾,可以让学生初步了解微积分的基本框架,使其更有兴趣去学习和掌握这门重要课程。另外,在高等数学教学中适时地穿插一些数学发展的历史和故事,通过成功数学家的实例阐述科学家是如何提出问题、思考问题和解决问题的。展现数学知识的产生背景,数学概念的形成和发展过程,以及数学定理的提出过程,可以提高学生学习数学的兴趣,加强学生对相关知识的理解。比如,在讲述无穷小的内容时,就可以引出历史上的第二次数学危机。无穷小是零吗?这个问题笼统地说就是贝克莱悖论。贝克莱指出:“牛顿在求导数时认为无穷小既等于零又不等于零,召之即来,挥之即去,这是荒谬的。”没有清楚的无穷小概念,使得导数、微分、积分等概念不清楚,无穷大概念也不清楚,而且导致了发散级数求和的任意性,符号的不严格使用,以及不考虑连续就进行了微分,不考虑导数及积分的存在性和函数可否展开成幂级数等问题。
通过了解第二次数学危机,对照高等数学教材中无穷小的概念,学生可以加深理解:无穷小不是零,是一类趋向于零的函数,常数零也是一类特殊的无穷小。
三、强调实际应用
虽然学校和老师一直强调高等数学很重要,但是学生往往对数学的重要性还没有足够的认识,这表现在他们对学习数学目的不明确,缺乏学习动力,对学习数学有一定的恐惧心理。他们认为学习数学就是记住其中的定义和定理,做大量习题或者记住大量习题的解法,这样在考试中就能取得好的成绩。大部分学生感到数学枯燥乏味,学习数学的积极性不高,有些学生甚至在学习上产生了困难,对数学产生了厌倦情绪。因此,授课老师要让学生改变这种错误认识,让他们切身感受到我们学数学不仅仅是纸上谈兵,它在很多学科中都有应用,从而提高学生学习数学的兴趣。
比如,函数的极值和最值问题是高等数学中的重要内容,在这方面有大量的的例题和习题。对于利用函数的导数研究函数的极值,学生不难掌握,但是如果没有应用类的问题则很难体现这种方法的应用价值。博弈论相对于数学来说是一门年轻的科学,现在它在生物学、经济学、计算机科学、军事战略和其他很多学科都有广泛的应用。下面我们通过一个博弈论中的模型来说明函数极值方法的应用。
例(古诺模型)设市场有1、2两个寡头厂商,生产并销售同一产品。他们的产量分别为q1,q2,边际成本分别为c1,c2,无固定成本。市场的逆需求函数为

其中a>ci(i=1,2)是一个固定常数,即该产品的市场最高价格。
假设两产商对市场需求和他们的成本和收益都是共同知识,并且在事先没有任何约定和协议的前提下,试确定使他们收益最大的产量。
解厂商的收益就是他们的利润函数,分别为

显然π1,π2都是关于q1,q2的连续函数,收益最大就是求π1,π2的最值.

则(q1*,q2*)是两厂商的最佳选择,即该博弈的平衡局势或称为纯策略纳什均衡点。
从求解过程中可以看出,这里实际上使用了非常基础的高等数学的方法。在更加复杂的博弈论模型的求解中,同样也会用到高等数学的这些方法。例如,在微分对策中研究的大部分模型,它们的求解过程实际上就是求解条件极值问题的拉格朗日乘子法。
四、注重几何直观的引入
微积分的创立首先是为了解决17世纪遇到的科学问题,这些问题有着很强的物理背景或几何背景。在解决这些问题的过程中抽象出来的微积分的概念和结论,都有一个从直观洞察到逻辑严密化的过程。可以说,具体应用微积分解决实际问题依然需要把现实问题抽象的模型同这些直观相匹配,通过几何直观领悟这些概念和结论的数学内涵依然是一条有效途径。


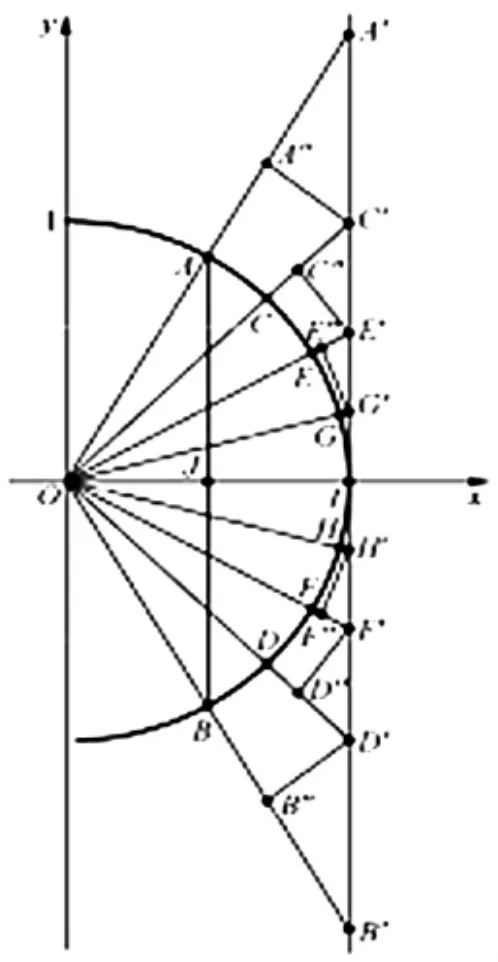
图1
上述解释,除用到极限的性质外,同时为定义一般曲线弧长埋下伏笔。而弦AB与弧A(B长度之比的极限是,恰是极限情形下“曲”化为“直”的一个基本实例。
借助几何直观能够揭示概念的本质,帮助理解定理的内涵。高等数学中还有很多内容,比如微分中值定理、隐函数存在定理、条件极值等都可以借助几何直观理解。几何直观虽然不能代替严格的证明,但几何直观的运用使得高等数学的学习变得简单,容易被学生接受。
总之,在高等数学的教学过程中,应该根据学生的特点和水平,选用能够激发学生学习热情的教学内容,采取适当的启发学生积极思维的教学方法,让学生主动地去探索数学真理,培养学生学习数学的兴趣和刻苦钻研数学问题的热情,引导学生敢于和善于发现问题或提出问题。
:
[1]克莱因.古今数学思想(第一册)[M].张理京,张锦炎,译.上海:上海科学技术出版社,1979
[2]同济大学数学系.高等数学(第6版)[M].北京:高等教育出版社,2007
[3]汪贤裕,肖玉明.博弈论及其应用[M].北京:科学出版社,2008
[4]李晓奇.先驱者的足迹—高等数学的形成[M].沈阳:东北大学出版社,2004
中图分类号:G642
B
1671-6531(2012)11-0103-02
江苏省教改基金项目资助(340912101);苏州科技学院青年科学基金项目资助
:姚 旺
