基于总体最小二乘的核四极矩共振参数估计

朱凯然 何学辉 郑小保 苏 涛

（1.西安电子科技大学雷达信号处理国家重点实验室，陕西 西安 710071；2.中国电波传播研究所，山东 青岛 266107）

引 言

进入21世纪后，反恐安全检测技术已成为人们的热点话题，同时也成为国防安全中重要的一部分，其目的是要把恐怖活动遏制在未遂状态。纵观这些恐怖活动，爆炸仍旧是恐怖分子使用的最主要方式，对爆炸物的及时有效探测是反恐活动的重要环节。

核四极矩共振 （NQR）是一种固态射频技术［1-9，11-16］，它可以用于检测四极矩原子核的存在性，例如普遍存在于爆炸物中的氮14原子核，它可作为一种判决依据对爆炸物进行探测。通过检测氮14原子核的NQR信号，不但可以判定爆炸物的存在性，而且还可以根据NQR谱线特征确定是何种爆炸物，可以说NQR信号是爆炸物的“指纹”。

NQR信号通常分为两种类型。一种称为自由感应衰减（FID）信号［12］，它是由单脉冲激励得到的信号；另一种称为自旋回波串信号［6］，它是由激励脉冲串激励得到的信号，可以在短时间内使NQR信号获得更高的信噪比。然而，NQR信号本身非常弱，并且易受线圈内热噪声和外部射频干扰（RFI）的影响，故此NQR信号极低信噪比制约了NQR技术在爆炸物探测方面的应用。文献［1］应用非线性最小二乘法提高信噪比，该方法在已知信源个数的前提下，建立NQR信号模型，在频率维和衰减系数维进行穷举搜索，计算量大，且需要先验信息。文献［9］运用基于最小二乘法的线性预测方程估计NQR信号的参数。本文采用基于总体最小二乘法［10］的线性预测方程对NQR信号的参数进行估计，该方法大大降低了计算量，且无需先验信息；在计算线性预测系数时，它克服了普通最小二乘法未考虑扰动对数据矩阵的影响，获得了更好的估计性能。

1.信号模型

窄带接收机接收到的FID信号可以表示成一个指数衰减的正弦信号［1］，表达式为

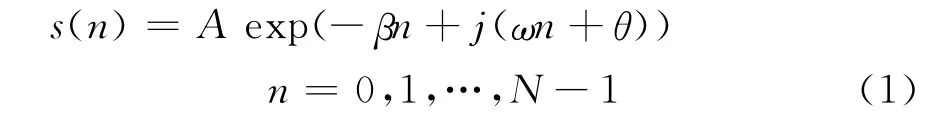
式中:A、β、ω和θ分别为FID信号的幅度、衰减系数、频率以及初相；ω通常是环境参数的函数，如温度。假设

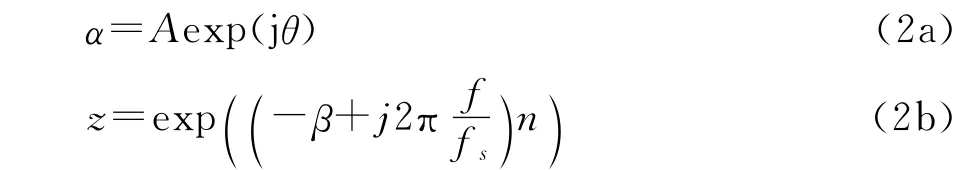
式中:f，fs分别表示FID信号频率和采样率。式（1）变为

实际观测数据可以表示为

式中:IN，wN分别表示干扰信号和噪声信号，均为N×1的向量；（·）T表示转置。式（4）可以看作在色噪声背景下，FID信号参数估计问题。

2.基于总体最小二乘的参数估计

在求解矩阵方程Ax=b的时候，普通最小二乘是用一个范数平方为最小的扰动向量e去干扰数据向量b，以校正b中存在的噪声，当A和b二者均存在干扰时，求解矩阵方程Ax=b的最小二乘方法将会导致大的方差，此时，需要同时考虑矩阵A和向量b中的扰动，即求解矩阵方程（A+E）x=b+e，这就是总体最小二乘方法的基本思想。由式（4）构造线性预测方程为

A为（N-L）×L 的 Hankel矩阵；x=（x1，x2，…，xL）T为线性预测向量；b=（y0，y1，…，yN-L-1）T.构造增广矩阵B=［b，A］，对矩阵B进行奇异值分解（SVD）

式中:U=［u1，u2，…，uN-L］∈C（N-L）×（N-L）；均为正交矩阵；奇异值矩阵

其奇异值按照降序排列，即σ1≥σ2≥…≥σq＞σq+1≈…≈σL+1，且q≤min（N-L，L+1）是增广矩阵B的有效秩；（·）H为共轭转置。那么，式（5）的总体最小二乘解为

式中:S-（q）是矩阵的S（q）逆矩阵，且

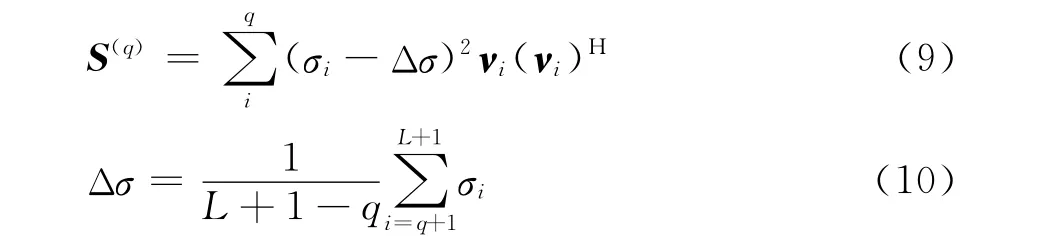
式中:S（q）为（L+1）×（L+1）维矩阵；νi是酉矩阵V的第i列。

得到xTLS后，由式（5）中任意一个差分方程可得特征多项式

解得式（11）的根zi，i=1，…，L，由FID信号的衰减特性知，寻找 Re（ln（zi））＜0，i=1，…，L 的根zi，i=1，…，p，那么，式（3）可简化为幅度参数a的线性方程，用矩阵形式表示为

式中，Z是N×p维Vandermonde矩阵。由于zi各不相同，那么Vandermonde矩阵Z的各列线性独立，可得式（12）的最小二乘解为

式中:Z†=（ZHZ）-1ZH是Z的伪逆矩阵。依据

可求得幅值、相位、衰减因子和频率。

得到p组信号分量估计参数后，依据最大似然估计准则

式中:Zi是Z的第i列；‖·‖2为2-范数。对应于J最小的那组参数，便是所求参数。式（17）的最小值可以转化为求式（18）的最大值，即

式中:Πz=Z（ZHZ）-1ZH.

此时，可以获得未知噪声模型下的信噪比估计为

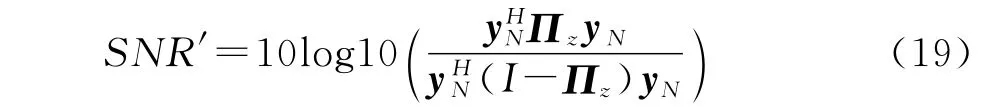
SNR′或称之为检测增益，它表征了NQR信号能量与背景噪声能量之比。

值得注意的是，式（5）的最佳线性预测器的参数等效于自回归（AR）模型的参数，最小预测误差功率也就等于激励的白噪声功率，此时的线性预测器也有白化滤波的作用。式（9）中减掉Δσ项，也具有消除噪声的作用。本文方法的步骤可归纳如下:

步骤1 根据式（5）与式（6）构造线性预测方程，线性预测器阶数通常取L≈N／3.

步骤2 计算增广矩阵B的SVD，并存储右奇异矩阵V；确定B的有效秩q；利用式（10）和式（9）计算矩阵S（q）；求S（q）的逆矩阵S-（q）；由式（8）得到线性预测器的系数xTLS.

步骤3 由式（11）解得特征多项式的根，zi，i=1，…，L，依据 Re（ln（zi））＜0，i=1，…，L 可以得到根zi，i=1，…，p，构造N×p维Vandermonde矩阵Z.

步骤4 由式（15）得到幅度信息的最小二乘解。

步骤5 由式（16）可以得到幅值、相位、衰减因子以及频率信息，依据式（18）、式（19）分别可以确定FID信号的参数和检测增益。

3.计算机仿真结果

应用基于总体最小二乘法的线性预测方法估计得到的NQR参数结果与文献［9］的方法进行比较。从仿真数据和实测数据两方面进行仿真，并比较上述两种方法的参数估计性能。

3.1 仿真数据

在室温下，采集背景噪声数据，然后加入相对于背景噪声不同信噪比（SNR）下的NQR模拟信号，生成仿真数据。根据黑索金（RDX）实测数据给出NQR模拟信号的参数:频率为2.3kHz，衰减常数为0.0064，初相位为30°，采样率为156.25kHz，信噪比从-5dB变化到20dB，步长为0.5dB.每个信噪比对背景噪声样本（22000个脉冲）进行100次随机不重复抽取（2000个脉冲）累加实验。

随着信噪比的变化，参数估计值如图1所示。其中，图1（a）为幅度信息估计，在高信噪比下，两者估计值均接近于理论值；图1（b）为衰减系数估计，随着信噪比的增加，估计值趋于真实值，若以衰减系数为检测变量，那么在较低信噪比下，本文方法优于文献［9］的方法；图1（c）为频率估计值，随着信噪比的增加，估计值也趋于真实值，本文方法优于文献［9］的方法；图1（d）为初始相位估计值，随着信噪比的增加，估计值也趋于真实值；文献［9］方法估计值更接近于真实值。图1（e）为检测增益，本文方法得到的检测增益优于文献［9］方法约0.8dB.

3.2 实测数据

实测数据源于研究RDX的FID信号特性实验［13-16］。探测RDX谱线频率为3.411MHz，在该共振频率下，其自旋-晶格弛豫时间在环境温度为283～295K 条件下大约为12ms［6，8］，自旋-自旋弛豫时间约为8ms.室温下，将300g RDX置于封闭的感应线圈内，用激励脉冲宽度为130μs，脉冲间隔为64.1ms（约大于5倍自旋-晶格时间）的单脉冲序列激励RDX.中心频率为100kHz，采样率为1.25 MHz.

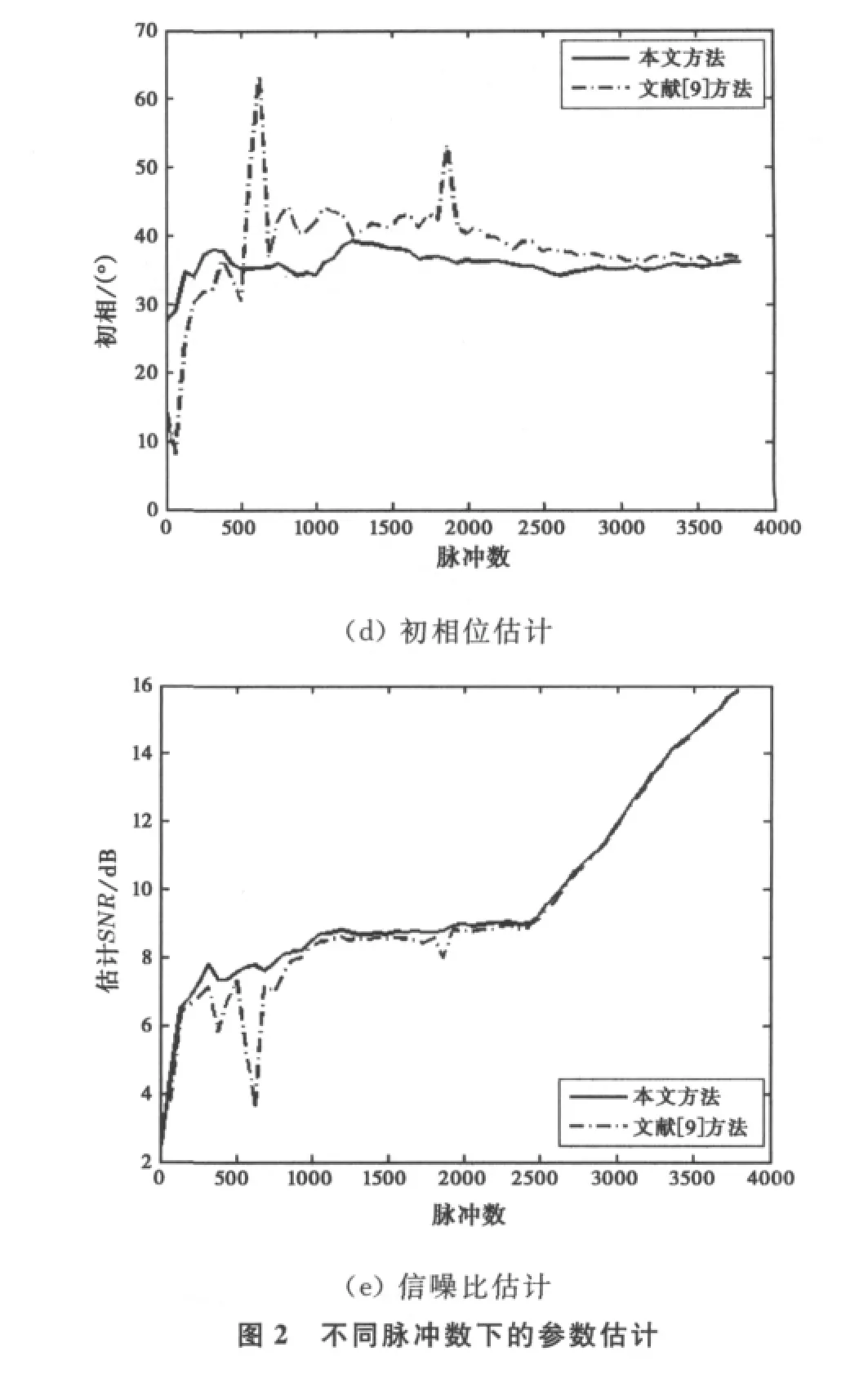
处理中，选取第一个数据文件内第一个脉冲为起始脉冲，以步长为62个脉冲顺序增加脉冲数，进行脉冲相干积累。理论上，N个等幅相干信号进行相干积累，可以使输出信噪比改善N倍。但实际上，由于相邻回波信号的相位相干性难以保证，因此信噪比改善一般达不到N倍［1，11-12］。不同积累脉冲数下，两种方法的FID信号参数估计性能比较如图2所示。图2（a）和图2（d）说明了脉冲相干积累的可能性，因为随着脉冲数的增加，幅度信息也随之线性增加，初始相位趋于稳定，初始相位的平均值为35.82°.图2（b）为FID信号的衰减系数估计，趋于0.007，而文献［9］方法表现出较大的波动。图2（c）为FID信号的频率估计，趋于2.35kHz.图2（e）为信噪比估计值，当积累脉冲数小于2500个时，对应的信噪比估计值小于10dB，文献［9］方法低于本文方法，大于2500个时，两种方法的性能一致，且趋于线性增加。综上，在较低信噪比下，与基于普通最小二乘法的文献［9］方法相比，本文方法呈现出较好的参数估计性能，同时也验证了FID信号模型的正确性。

4.结 论

在研究RDX的FID信号特性的基础上，针对NQR信号参数的估计问题，应用基于总体最小二乘法的线性预测方法，并考虑了线性预测方程左右扰动矩阵的影响，获得了较好的参数估计性能。但该类线性预测方法也有不足之处，当数据长度较大时，数据矩阵的行数太大，且为了得到好的预测系数，通常需要很大的线性预测阶数。NQR技术是一种有效的检测爆炸物技术，具有良好的发展前景，NQR信号极低信噪比一直是制约该技术在爆炸物探测方面应用的瓶颈，研究低信噪比下爆炸物检测算法成为亟待解决的问题。下一步的工作，将进一步研究FID信号特性，稳态自由振荡脉冲序列（SSFP）回波信号特性，自旋锁定脉冲序列（SLMP）回波信号特性以及低信噪比下爆炸物检测算法。

［1］JAKOBSSON A，MOSSBERG M，ROWE M D，et al.Exploiting temperature dependency in the detection of NQR signals［J］.IEEE Transactions on Signal Processing，2006，54（5）:1610-1616.

［2］TAN Yingyi，TANTUM S L and COLLIN L M.Landmine detection with nuclear quadrupole resonance ［C］／／IEEE International Geoscience and Remote Sensing Symposium，2002，3:1575-1578.

［3］SOMASUNDARAM S D，JAKOBSSON A，and BUTT N R.Countering radio frequency interference in single-sensor quadrupole resonance［J］.IEEE Geoscience And Remote Sensing Letters，2009，6（1）:62-66.

［4］SOMASUNDARAM S D，JAKOBSSON A，ROWE M D，et al.Robust detection of stochastic nuclear quadrupole resonance signals［J］.IEEE Transactions on Signal Processing，2008，56（9）:4221-4229.

［5］TAN Yingyi，TANTUM S L，and COLLIN L M.Cramer-Rao lower bound for estimating quadrupole resonance signals in Non-Gaussian noise［J］.IEEE Signal Processing Letters，2004，11（5）:490-493.

［6］RUDAKOV T N，MIKHALTSEVITCH V T，and FLEXMAN J H.Modified steady-state free precession pulse sequences for the detection of pure nuclear quadrupole resonance［J］.Solid State Nuclear Magnetic Resonance，2004，25（1-3）:94-98.

［7］GARROWAY A N，BUESS M L，MILLER J B，et al.Remote sensing by nuclear quadrupole resonance［J］.IEEE Transactions on Geoscience and Remote Sensing，2001，39（6）:1108-1118.

［8］SMITH J A S.Nitrogen-14quadrupole resonance detection of RDX and HMX based explosives［C］／／European Convention on Security and Detection.London，1995:288-292.

［9］GRECHISHKIN V S，GRECHISHKINA R V，and HEO H.Signal prcessing methods in NQR ［C］／／Explosives Detection Using Magnetic and Nuclear Resonance Techniques，NATO Science for Peace and Security Series B:Physics and Biophysics.2009:159-170.

［10］张贤达.矩阵分析与应用［M］.北京:清华大学出版社，2004:403-452.

［11］赵振维，娄 扬，金燕波，等.基于自适应滤波技术的 NQR信号处理［J］.电波科学学报，2008，23（3）:429-433.ZHAO Zhenwei，LOU Yang，JIN Yanbo，et al.Signal processing for NQR based on adaptive filtering［J］.Chinese Journal of Radio Science，2008，23（3）:429-433.（in Chinese）

［12］原 普，毛云志，郭华民.爆炸物检测中微弱NQR信号的处理［J］.电波科学学报，2006，21（2）:204-208.YUAN Pu，MAO Yunzhi，GUO Huamin.Weak signal receiving and processing for nuclear quadrupole resonance detection［J］.Chinese Journal of Radio Science，2006，21（2）:204-208.（in Chinese）

［13］夏佑林，叶朝辉.14N核四极共振中自旋锁定的偏共振效应［J］.物理学报，1995，44（6）:970-976.XIA Youlin，YE Chaohui.Offset effects of spin-locking in14N nuclear quadrupolar resonance［J］.Acta Physica Sinica，1995，44（6）:970-976.（in Chinese）

［14］夏佑林，叶朝辉.14N核四极共振自旋系统自旋-晶格弛豫时间的测量［J］.波谱学杂志，1994，11（4）:327-355.XIA Youlin，YE Chaohui.The measurments of spinlattice relaxation times for a14N nuclear quadrupolar resonance spin system［J］.Chinese Journal of Magnetic Resonance，1994，11（4）:327-355.（in Chinese）

［15］夏佑林，叶朝辉.自旋I=1和3／2的粉末样品的核四极共振波谱学—I.对脉冲的响应［J］.自然科学进展，1995，5（4）:467-473.

［16］夏佑林，叶朝辉.自旋I=1和3／2的粉末样品的核四极共振波谱学—II.核四极共振回波及应用［J］.自然科学进展，1995，5（5）:559-464.