基于正交编码的高频地波雷达信号的设计
2012-09-18李超张宁
李 超 张 宁
(哈尔滨工业大学电子工程技术研究所,黑龙江 哈尔滨 150001)
引 言
解决电离层杂波折叠就是要提高信号的不模糊距离,使得电离层杂波处在信号的不模糊距离之外,无法对探测距离内产生折叠效应。虽然加大脉冲周期可以增大不模糊距离,却会导致占空比下降,从而使得发射机功率降低无法实现远距离探测。若采用多脉冲正交信号,由于脉冲之间相互正交,即其互相关函数为零,回波信号经过脉冲压缩之后,只对自身脉冲产生距离谱,因此,不产生距离模糊。简单的正交编码往往不具有好的自相关函数特性,无法达到雷达目标检测的需求;若采用正交矩阵得到多脉冲编码,虽然具有良好的旁瓣特性,但由于脉冲周期过长,容易产生多普勒模糊,无法满足海空兼容探测。因此,需要进行正交编码波形优化设计。
发射波形优化设计是众多学者近年来的研究热点。Deng[1-2]研究了基于模拟退火的正交波形设计,主要是以互相关和自相关旁瓣能量最小为目的。在Deng的研究工作之后,出现了一系列正交波形设计方法,其中主要有遗传算法、整数非线性规划、最小互熵法、相位逗留法等,这些方法被广泛用于多输入多输出(MIMO)雷达[3-4]和分组雷达信号的设计。然而,这些雷达均采用频分复用来发射多频信号。对于高频地波雷达系统来说,频分复用信号对设备的线性度要求很高,且信噪比损失较大,时分复用方式是首选。本文主要研究高频地波雷达时分复用方式下正交编码的设计,其各个频段采用的信号形式完全相同,要求每个频段内信号的各个脉冲正交。
高性能的雷达系统通常要求峰值旁瓣比达到-30dB以上,在一些特殊的场合有可能提出超低旁瓣的要求。当优化设计的编码仍无法满足系统对旁瓣的需求时,就需要采用信号处理的手段来降低旁瓣。目前国内外关于旁瓣抑制滤波器的设计方法很多,如窗函数加权法[5,6],最小均方误差(LMS)[7],最小的线性规划法,递归最小平方法(RLS)[8]以及近年来兴起的神经网络算法等。早在1971年,Rihaczek和Golden[9]就利用反相滤波器对Barker码进行抑制,取得了较好的效果,但由于只考虑对Barker码的抑制,限制了其广泛应用。G.D.Cain[10]等提出了基于反相滤波的最优码搜索。随后Erikmat[11]又提出了利用无限长脉冲响应(IIR)来设计反相滤波器。Robert C[12]详细地分析了Erikmat的算法并利用在旁瓣抑制方面。
针对高频地波雷达的特殊需求来构建代价函数,采用遗传算法设计时分复用的正交双脉冲信号,获得了具有理想自相关函数旁瓣和互相关函数峰值的信号。并对得到的正交编码采用反相滤波算法进行了旁瓣抑制。通过仿真实验比较,可以看出此算法的抑制性能更为有效。即使在较大多普勒偏移下仍有较低旁瓣,完全可以满足高频地波雷达系统需求。
1.电离层杂波产生的折叠干扰问题
电离层杂波折叠[13,15]是指发射信号以一定角度到电离层向外传播,由于信号总路径必定经过了由脉冲重复间隔决定的最大探测距离。因此,雷达会将前几个脉冲的回波在当前周期中接收回来,产生距离模糊。由于存在着距离模糊,与目标同一距离单元上接收到的杂波在时间上是重叠的,其中包括近程的强杂波。高强度的折叠杂波完全有可能淹没目标,尤其是复杂低空环境中的弱目标。如果系统无法检测折叠杂波中的目标,就会发生目标丢失现象,影响到雷达的探测性能。
微波雷达工作在微波段,信号可以穿透电离层杂波,因此,电离层杂波对微波雷达探测目标几乎没有影响。而对于高频地波雷达来说,其作用距离为300~400kg.几千公里外的电离层杂波折叠,对这一区域目标产生严重的干扰。因此,电离层杂波折叠问题可以说是高频地波雷达波形设计中必须要考虑的问题。
从波形设计的角度解决高频雷达的电离层杂波折叠干扰问题,方法主要有两种:
1)单脉冲叠加相位旋转。文献[13]针对高频雷达中杂波折叠问题,提出了一种脉间相位编码波形,将杂波搬移到无目标存在的多普勒区间,使原本掩盖的目标显现出来。从而解决了电离层杂波的折叠干扰问题。但是这种方法需要目标的先验知识。
2)正交多脉冲序列。文献[14]用Frank矩阵等正交矩阵构造正交多脉冲互补编码,这种编码脉压信号具有零旁瓣特性,且能将不模糊距离推远到几千公里以外,避免了电离层对回波产生影响。
但是以上两种方法都有其自身缺陷,单脉冲序列脉冲压缩信号往往具有过高旁瓣,无法满足我们的检测需求。正交互补序列由于其互补特性,有着理想的脉压主旁瓣比,但是其分段互补的信号结构,使得信号的重复周期过长。当采用多频分时探测模式时,无法进行海空兼容探测。为了同时满足高频地波雷达的这些需求,采用优化算法来设计双脉冲正交信号,解决电离层杂波折叠问题,并保证足够的占空比,同时其信号参数可以实现多频模式下的海空兼容探测。双脉冲正交信号的不模糊距离如图1中Ru所示。

图1 双脉冲正交信号不模糊距离示意图
如图1所示,双脉冲正交信号由两个相互正交的脉冲组成一个信号周期。脉冲串(a)为发射信号,脉冲串(b)为回波信号。如果是单脉冲信号,就无法区分回波信号的第2个脉冲是发射信号的第1个脉冲的时延(Tp+Δt)还是第2个脉冲的时延(Δt).因此,模糊距离为.但对于双脉冲正交信号,由于两个脉冲相互正交,即其自相关函数为零。回波信号经过脉冲压缩之后,只对自身脉冲产生距离谱,因此不产生距离模糊。其最大不模糊距离为信号周期即Ru=2×=.因此,按照高频地波雷达的检测需求来构造代价函数得到双脉冲正交信号就可以解决电离层杂波折叠的问题。
2.基于遗传算法的正交相位编码
利用遗传算法设计正交码,就是针对实际系统综合考虑多方面构造出代价函数,并最小化代价函数得到编码序列。
2.1 代价函数的构造
为了满足海空兼容探测的需求,主要研究了双脉冲正交相位码。设有一对长度相同的有限二元序列,

信号的自相关函数为式(1)和式(2),互相关函数为式(3).

码元信号需要具有以下特性:
1)每个脉冲都具有较低的峰值旁瓣电平PSL


2)每个脉冲具有较低积分旁瓣电平ISL
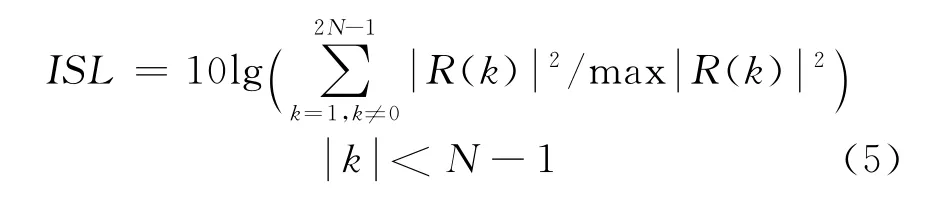
3)两个脉冲的互相关函数峰值较低(低于各自的自相关旁瓣)

需要说明的是,这里对互相关函数用自相关函数峰值进行归一化,若归一化的互相关函数峰值低于自相关函数旁瓣,则表明两个脉冲正交,信号重复周期(两个脉冲周期)内不存在距离模糊现象,信号的最大不模糊距离为两个脉冲周期。
4)两个脉冲的互相关函数积分旁瓣电平较低

将以上各个约束函数以罚函数的形式附加到代价函数中,则有

式中:[w1,w2,w3,w4]是各个约束函数的加权系数,可以通过训练的方法得到,也可以根据优化要求自行设置。
2.2 遗传算法设计正交编码步骤
1)编码
把一个问题的“可行解”从“解空间”转换到遗传算法所能处理的“搜索空间”的转换方法就称为编码。近年来许多学者研究证明二进制码比十进制码具有更强的搜索能力。因此,二进制编码是遗传算法中最主要的一种编码方式。
由于需要优化设计的二相码本身就是二进制编码,因此可以直接将它们表示成遗传空间的基因型数据。这里把两个脉冲的编码放在一个行矩阵中,看成一个个体。即S=[C1C2]=sn,sn∈ (0,1),n=1,2,…,2 N,N为二相正交码一个脉冲内的码元个数。S前一半码元为第一个脉冲C1,后一半码元为第二个脉冲C2.
2)初始群体的生成
由于遗传算法的群体型操作需要,必须为遗传操作准备一个由若干“初始解”组成的初始群体。若初始种群数量为NIND个,每个脉冲内码元个数为N,采用随机二元码做编码。则初始种群为NIND×2 N的矩阵。
3)计算适应度
在完成编码和初始化种群后,将种群中每个个体的编码带入代价函数中计算其适应度值。计算的适应度值为后面的操作提供依据。
4)选择
根据第三步计算出的适应度值对种群中的个体进行选择,适应度高的个体遗传到下一代的概率就较大。常用的选择算子有轮盘赌、随机竞争、最佳保留等。本文选择随机遍历法进行搜索。
5)交叉
在遗传算法中,交叉是产生新个体的主要手段,将第四步选择的个体进行离散重组和交叉。
6)变异
变异是按位进行的,即把某一位的内容进行变异。变异操作是十分微妙的操作,它需要和交叉操作妥善配合使用,目的是挖掘群体中个体的多样性,克服有可能陷于局部解的弊病。
7)终止
当完成遗传的代数后程序终止。
2.3 设计结果及性能
按照以上算法和步骤,进行仿真实验,优化设计正交相位编码,遗传算法仿真参数为:初始种群数量100,迭代最大次数200,代沟0.9,交叉概率0.7,为了保证信号的正交性,需要互相关函数峰值小于自相关函数旁瓣,因此权值设为w= [1131],脉内码元个数N为32.
图2为遗传算法200次迭代的性能跟踪。可以看出种群均值和最优解逐渐收敛,迭代次数越多,得到解的各项性能就越优,当收敛到一定程度,解的各项性能不随迭代次数增加而变化,实验证明迭代200次可以得到最优解。
每次运行遗传算法得到的最优解不尽相同,但是其自相关和互相关特性相差无几,这些最优解都可以作为高频地波雷达的编码。这里分析其中一组码元的性能。
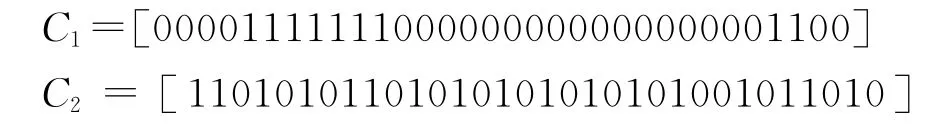
其自相关函数与互相关函数图如3和4所示。

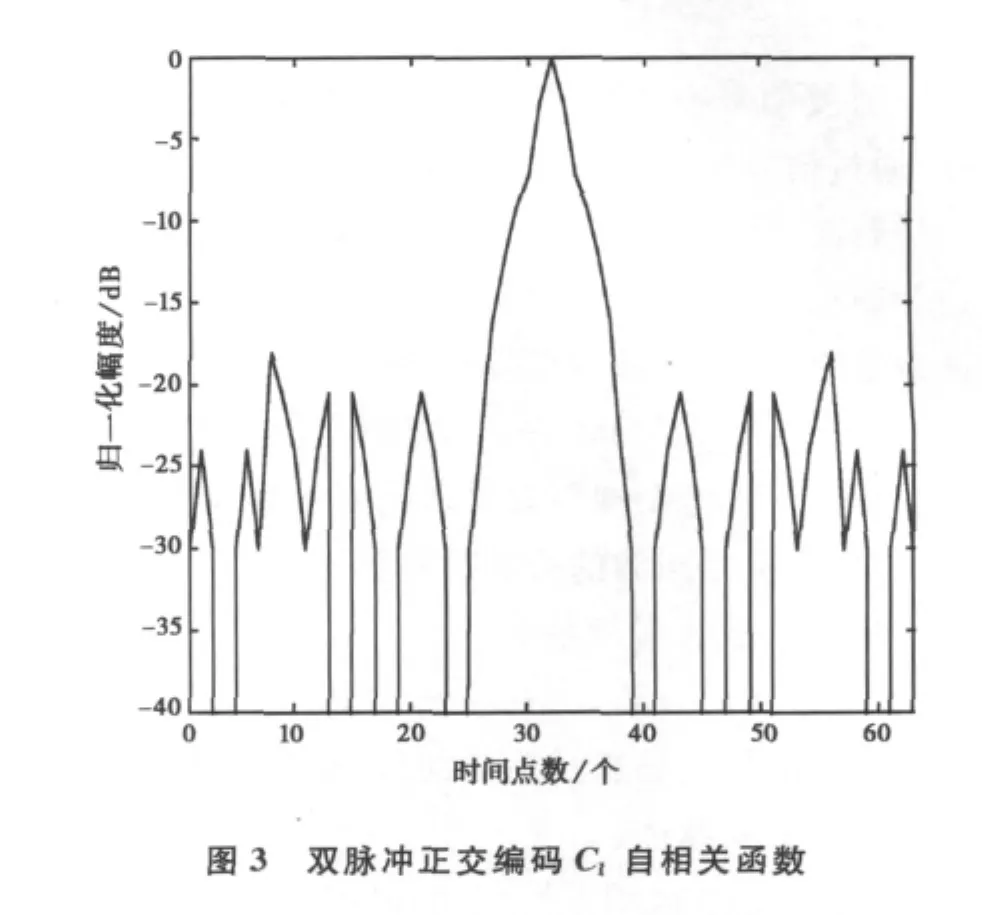
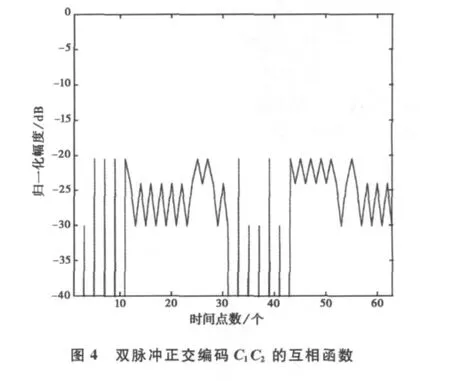
从图4可以看出,两个脉冲的互相关函数峰值-20dB,小于各脉冲的自相关峰值-18dB,这样就不会产生距离模糊现象。最大不模糊距离为两个脉冲周期。因此,采用遗传算法可以得到解决距离模糊现象的正交相位编码。但是高频地波雷达对脉压信号的峰值旁瓣有较高的要求,通常需要在-30dB以上。而通过优化算法得到的正交编码自相关函数旁瓣大约都在-20dB左右,因此必须要进行旁瓣抑制。
3.正交编码信号的旁瓣抑制
在雷达信号的接收端,需要对回波信号进行处理得到需要的距离速度谱。双脉冲的信号处理方法如图5所示。

图5 双脉冲信号的处理方法
回波信号经过降采样和滤波之后,进行脉冲选择,通过信号识别算法判断出回波是第几个脉冲,然后进行匹配滤波,得到距离谱,根据目标特性,选择适当的积累时间进行脉冲积累得到速度谱。为了提高信号的分辨力,进一步降低旁瓣,必须进行旁瓣抑制,本文采用Erikmat提出的反相滤波算法[11],仿真实验证明其旁瓣抑制效果远远好于其他算法。
3.1 基于反相滤波的旁瓣抑制算法
回波信号的Z变换为

算法的核心思想是信号经过旁瓣抑制滤波器之后应为零旁瓣脉冲。

Mercer指出,具有+1,-1系数的多项式至少有一个零点在单位圆上或单位圆外。因此,C-1(z)就有极点在单位圆外,不是稳定因果系统。Robert在文献[12]中把C(z)分成两部分:

信号长度N=M+L-1.这里P(z)为C(Z)所有单位圆内零点所构成的多项式。Q(z)为所有C(Z)单位圆外零点构成的多项式。
这样滤波器P-1(z)是稳定的。当信号通过如图6所示P-1(z)的部分时就去掉了单位圆内零点所产生的旁瓣,输出信号为F(z),理论上F(z)=Q(z).Q(z)的时间反向为

(Z)的零点是Q(Z)的零点的倒数,其零点都在单位圆内,滤波器响应是稳定的。编码序列经过滤波器P-1(z)后,进行时间反向操作,然后再经过(Z)滤波器,得到的期望响应为冲击单位抽样序列δ(n).这样,通过两个滤波器级联的方式,就可以完全的去处旁瓣。

图6 反相滤波器结构示意图
3.2 算法性能仿真实验
将正交编码进行匹配滤波,然后将匹配滤波得到的自相关函数转换成Z变换序列,求序列的零点。用在单位圆内的零点构造P-1(z)滤波器;将单位圆外的零点求倒数后构造(Z)滤波器。这样就可以得到反相滤波器组。
仿真实验采用脉冲宽度为20μs,编码长度为32,载频为14MHz(高频地波雷达通常为3~15 MHz)。将输入信号按照图6的方式通过滤波器组就得到旁瓣抑制结果。从表1可以看出经过旁瓣抑制后脉冲压缩信号峰值旁瓣非常低。

表1 几种旁瓣抑制方法的比较
表1将该算法与目前常用的算法进行了比较。可以看出,反相滤波算法在噪声背景下的滤波性能一般,但是也能够满足高频地波雷达信号检测的需要。而在其他情况下要远远优于其他算法。尤其是在多普勒频移较大的时候fd=23(载频为14 MHz,目标速度为250m/s)也具有-45dB的峰值旁瓣。
图7为目标在不同速度下,码反相滤波算法的旁瓣抑制性能,可以看出,即使在速度较高的情况下也能有较低的旁瓣,高速目标的旁瓣也能低于-40 dB,其多普勒容限性较好。

图7 码反相滤波算法的多普勒容限性
4.结 论
采用遗传算法设计正交编码,码元信号具有良好的自相关和互相关特性,解决了高频地波雷达电离层折叠的问题。为了进一步降低自相关函数旁瓣,研究了码反相滤波算法,仿真实验证明算法有着较好的抑制效果且多普勒容限性好,未来将对其的工程应用进行更细致的研究。
[1]DENG H.Poly Phase code design for orthogonal netted radar systems[J].IEEE Transactions on Signal Processing,2004,52(11):3126-3135.
[2]DENG H.Discrete frequency-code waveform design for netted radar systems[J].IEEE Signal Processing Letters,2004,11(2):179-182.
[3]LI Jian,XU Luzhou,STOICA P.Range compression and waveform optimization for MIMO radar:a cramerrao bound based study[J].IEEE Transactions on Signal Processing,2008,56(l):218-232.
[4]李树锋,张履谦.基于完全互补序列的正交MIMO雷达二维DOA估计[J].电波科学学报,2009,25(4):617-623.LI Shufeng,ZHANG Lvqian.Two dimensional DOA estimation for orthogonal MIMO radar based on complete complementary sequence[J].Chinese journal of radio science,2009,25(4):617-623.(in Chinese)
[5]KRETSCHMER F F,WELCH L R.Sidelobe reduction techniques for polyphase pulse compression codes[C]//IEEE International Radar Conference.Alexandria,VA,USA,2000:416-421.
[6]LUSZCZYK M,MUCHA D.Kaiser-bessel window weighting function for polyphase pulse compression code[C]//Microwaves,Radar and Wireless Communications,2008:1-4.
[7]PARK S C and DOHERTY J F.A mini-max optimization approach to sidelobe suppression filter design[C]//IEEE International Conference on Acoustics,speech,and signal processing,1996,6:3113-3116.
[8]张仕元,吴乐南.基于RLS的脉压雷达数字旁瓣抑制滤波器设计方法[J].测控技术,2006,25(7):79-82.ZHANG Shiyuan,WU Lenan.Design of digital sidelobe suppression filter based on RLS method[J].Measure and Control technology 2006,25(7):79-82.(in Chinese)
[9]RIHACZEK A W and GOLDEN R M.Range sidelobe suppression for barker codes[C]//IEEE Transaction on Aerospace and electronic system,1971,7:1087-1092.
[10]CAIN G D,YARDIM A,BOWLER A M,et al.Reducing pulse compression sidelobes by inversion amenable code selection[C]//Radar Conference.Roman,2008:1-6.
[11]ERIKMATS O.Range sidelobe elimination for discrete-coded pulse compression systems[C]//International Conference on Radar,1978:187-193.
[12]DANIELS R C and GREGERS-HANSEN V.Code inverse filtering for complete sidelobes removal in binary phase coded pulse compression system[C]//Radar Conference,2005:256-261.
[13]CLANCY J T,BASCOM H F,HARTNETT M P.Mitigation of range folded clutter by a nonrecurrent waveform[C]//IEEE Radar Conference,1999:79-83.
[14]KRETSCHMER F F,Jr,Gerlach K.Low sidelobe radar waveforms derived from orthogonal matrices[J].IEEE Transactions on Aerospace and Electronic Systems,1991,27(1):92-101
[15]万显荣,杨子杰,张景伟.高频地波雷达距离混叠与距离模糊研究[J].电波科学学报,2009,24(5):891-894.WAN Xianrong,YANG Zijie, HANG Jingwei.Range aliasing and range ambiguity of HF surface wave radar[J].Chinese Journal of radio science,2009,24(5):891-894.(in Chinese)
