大挠性空间桁架结构的动力学建模与仿真研究

周成刚,刘 军,宋石玉,杜海旺,顾 俊

(中国卫星海上测控部,江苏 江阴 214431)

0 引言

随着航天技术的进步,航天器结构的发展趋势是大型化、复杂化,大挠性空间桁架作为一种特殊的空间结构得到越来越广泛的应用。如和平号空间站和美国的SRTM系统采用一字型空间桁架,用于展开舱外天线设备,以此减少电子设备间的相互干扰[1]。另一方面,为降低发射费用,要求桁架结构尽可能轻。但受现有材料性能和太空工作环境的限制,以及要求空间结构具轻质、低刚度、低阻尼等特性,在轨工作时一旦受各种外部或内部的干扰易激起低频、大幅度、长时间的振动,同时因为低阻尼特性,激起的振动很难自行衰减。这种振动与航天器主体姿态运动相互耦合,会对卫星的定位精度产生严重影响。作为支撑结构的空间桁架的动力学性能对整体空间结构的性能影响尤为重要,因此研究大挠性空间桁架结构的动力学特性很有必要。

目前,国内外大挠性体模型多为有限元模型,并用实验方法对其进行验证研究。本文中针对航天器结构中普遍应用的一字型大挠性空间桁架(截面构型为正方形),在建立普通式和拉索式空间桁架结构简化模型的基础上,用有限元法对大挠性空间桁架结构进行建模,对动力学特性进行仿真研究。

1 建模

1.1 物理模型

以和平号空间站和SRTM系统的空间桁架为研究对象。为简化分析,作假设如下：

a)空间站及航天飞机质量较大,空间桁架结构为大挠性,质量远小于航天器,将与空间站及航天飞机连接的始端边界条件简化为固支。

b)忽略连接铰链的间隙影响及其自身刚度对整个桁架刚度的影响,不考虑非线性因素,将其简化为集中质量。

c)桁架结构末端电子设备简化为集中质量,作动器、传感器、铰链质量平均分配至各接头处。

d)整体桁架为杆结构。

e)空间环境简化为真空环境。

由此,建立本文一字空间桁架模型(截面构型为正方形)的仿真模型物理模型如图1所示[2-3]。

图1 大挠性空间桁架简化模型Fig.1 Simplified model of LFST

1.2 有限元模型

空间桁架模型由杆单元、梁单元、弦单元和集中质量单元组成。用线性或非线性有限元方法将各单元的刚度阵、质量阵和阻尼阵集成可得桁架结构的整体刚度矩阵K、整体质量矩阵M和整体阻尼矩阵C分别为

设系统阻尼为瑞利阻尼,建立模型的有限元动力学方程为

式中：δ为节点位移矢量;n为结构系统的总体自由度数;F(t)为系统的外激励力[4]。当外界激励为零,忽略阻尼影响,系统为自由振动,动力学方程可简化为。

2 仿真

根据大挠性空间桁架的简化模型,本文设计了两个采用铝合金材料的大挠性空间桁架结构有限元仿真模型,桁架结构尺寸0.4 m×0.4 m×4.8 m,分别由杆件213根和杆件132根及对角弦组装而成。令材料弹性模量72.7 GN/m2,密度3 100 kg/m3。桁架杆设计为空心管状结构,外直径0.012 m,内直径8 mm,等效横截面积A=6.283×10-5m2,桁架对角弦等效刚度k=1×106N/m,等效质量0.04 kg,张紧力T=100 N,接头质量0.4 kg,桁架顶端带质量块20 kg。杆件的惯性矩

式中：R,θ分别为极坐标系中的极半径和角坐标。杆件的极惯矩为

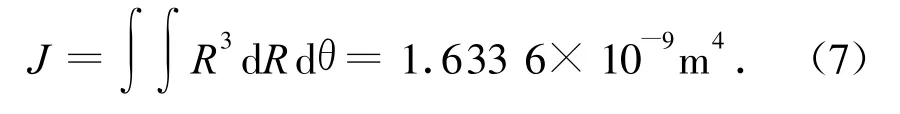
用有限元方法将整体桁架结构离散成节点68个、杆单元213个、集中质量单元68个。其中,集中质量单元模拟了接头的质量和顶端质量块,前4个节点为固支。考虑固定接头,空间桁架结构的杆件可简化为梁单元,有限元仿真模型即为空间梁系模型,建立有限元仿真模型如图2所示[5]。

图2 大挠性空间桁架结构的有限元仿真模型Fig.2 Finite element model of LFST

2.1 模态分析

2.1.1 模态频率

对顶端负载同一质量块(30 kg)的普通式和拉索式空间桁架进行模态振动频率计算,其前六阶模态振动频率见表1[6]。由表可知：由于物理结构的对称性,普通式和拉索式空间桁架的振动模态频率均有一定的规律性：1、2阶模态频率和4、5阶模态频率是两个大小相近的频率对;1、2阶模态频率对应空间桁架的一阶弯曲振型,振动方向相差90°;4、5阶模态频率对应空间桁架的二阶弯曲振型,振动方向相差90°;3、6阶频率单独出现,分别对应空间桁架的一阶、二阶扭转振型,如图3所示。

表1 大挠性空间桁架结构的振动频率Tab.1 Vibrating frequency of LFST

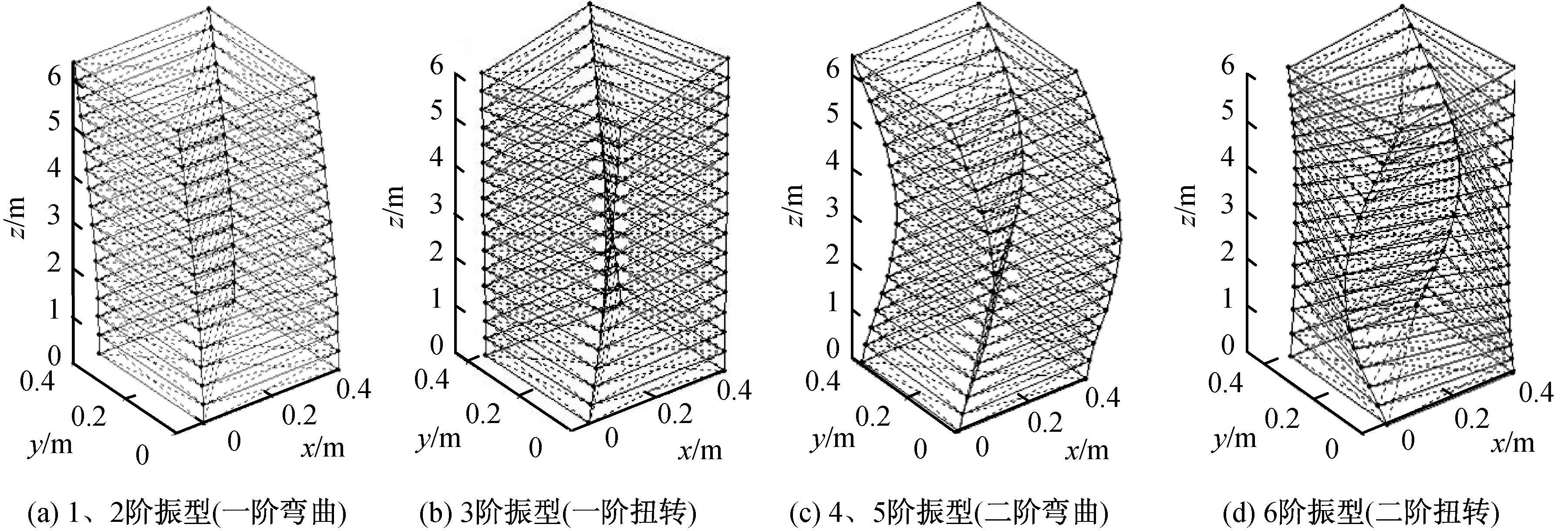
图3 大挠性空间桁架振型仿真结果Fig.3 Numerical simulation results of modal frequency of LFST

2.1.2 振型仿真

对普通式和拉索式空间桁架的振型分别进行仿真,所得规律类似,其中拉索式空间桁架的模态仿真结果如图3所示。

对拉索式空间桁架结构,为分析对角弦结构的预紧力对整体桁架结构自由振动频率的影响,在T分别为0,10,20,200 N条件下求解自由振动频率,计算结果如图4所示。

由图4可知：对角弦的预紧力对整体结构的自由振动频率影响较大,初始张紧力越大,低阶振动频率越小,且近似成线性关系;对角弦的预紧力对扭转模态频率的影响大于对弯曲模态的影响。

图4 不同对角弦预紧力时的自由振动频率Fig.4 Vibrating frequency with various diagonal f orce

2.2 谐响应仿真

设桁架顶端x轴正方向受到周期正弦激励F=10sin(2πf)N,在f分别为2,4,8,10 Hz条件下进行仿真,取节点30作为响应点,其x向位移响应如图5所示。

由图5可知：大挠性空间桁架结构受周期激励产生振动,当周期激励频率与桁架结构固有频率越接近,激起的振幅越大,即产生共振现象。

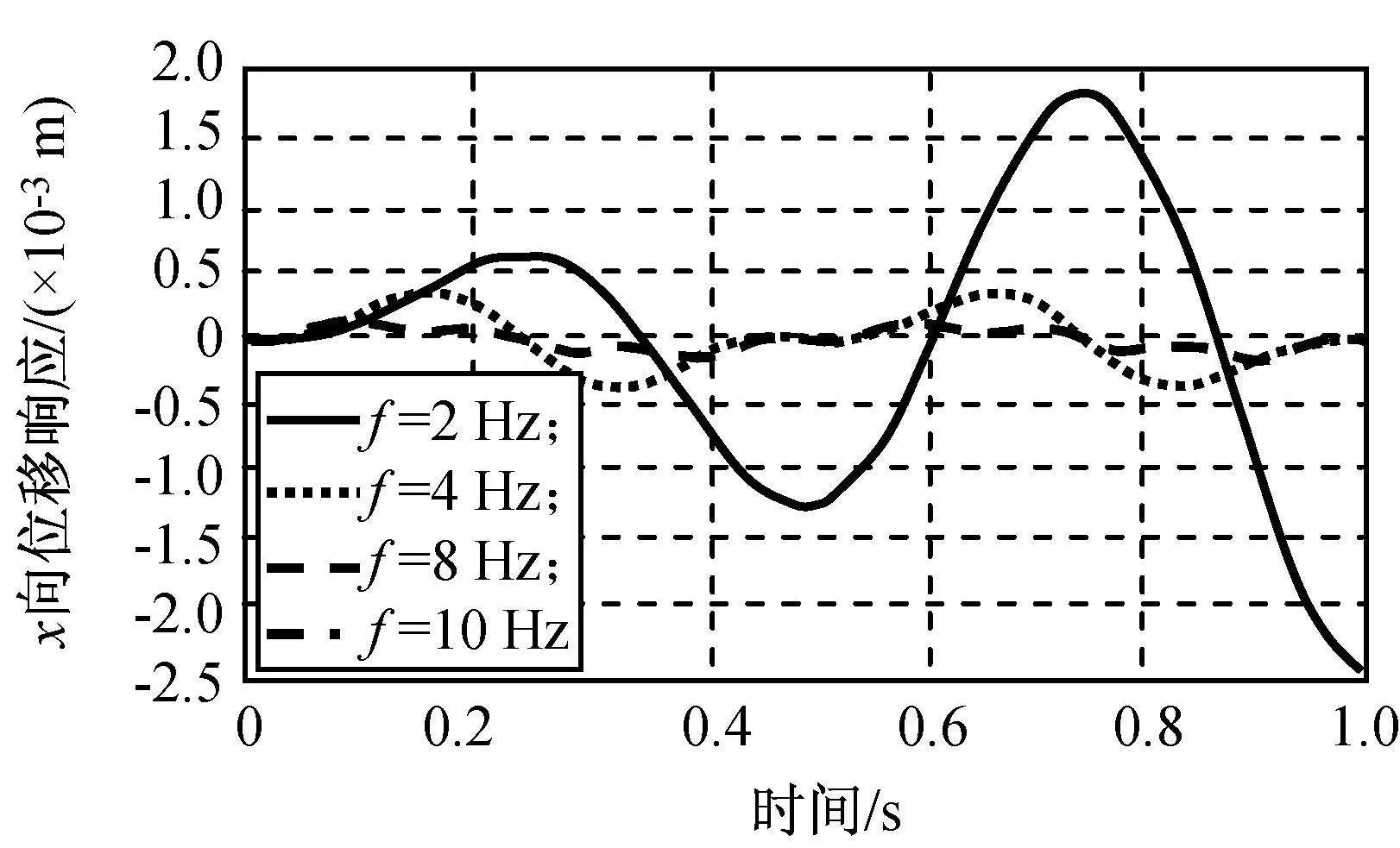
图5 空间桁架周期激励响应Fig.5 Periodic exciting response of LFST

2.3 脉冲激励响应仿真

大挠性空间桁架在轨工作时,可能会受到空间碎片、陨石的冲击而引起振动,这种冲击作用时间短、作用力较大,可认为是脉冲激励,因此研究大型挠性桁架脉冲激励响有其现实意义。

设系统阻尼为瑞利阻尼,前两阶振动阻尼比均为0.005,用瑞利阻尼计算公式可求得3～10阶模态的阻尼比相应为0.015,0.023 3,0.023 3,0.051,0.058 8,0.062 8,0.062 8,0.110 3[5]。令桁架顶端受x轴正向的冲击力大小100 N,作用时间为0.01 s,取节点30作为响应点,其x向位移响应如图6所示,图7为图6的局部放大。

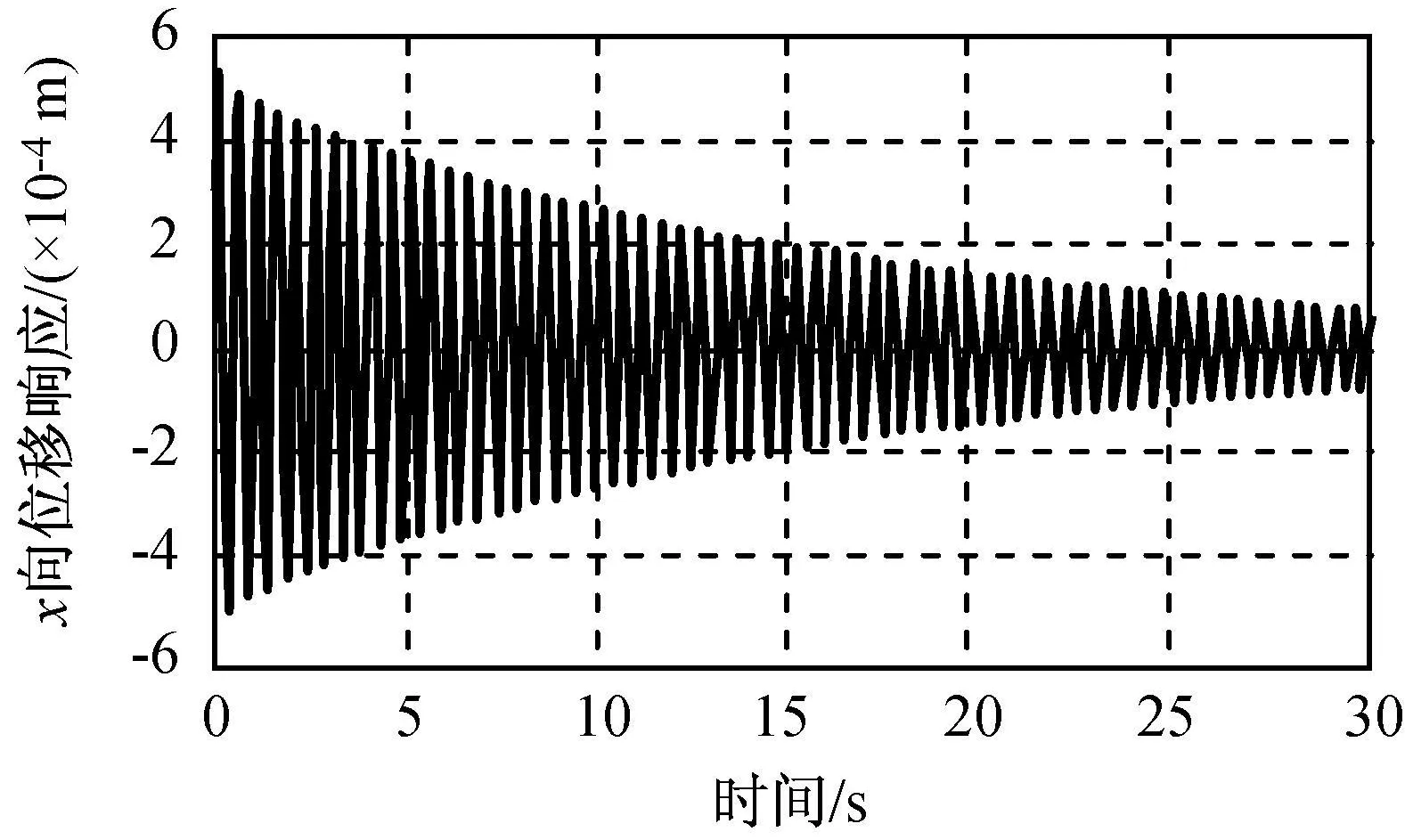
图6 空间桁架瞬态激励响应Fig.6 Transient exciting response of LFST

由图6、7可知：桁架结构受脉冲激励时产生振动,仅依靠自身阻尼衰减耗时很长(30 s时振幅衰减不足80%);激起的振动主要是一阶弯曲,高阶振动衰减速度明显快于低阶振动。

图7 图6局部放大Fig.7 Partial amplified of f igure6

3 结束语

针对典型的大挠性空间桁架结构,用有限元仿真法对模态特性、谐响应和脉冲激励响应进行了研究,并分析了拉索式大挠性空间桁架结构中对角弦的张力对其结构动力学特性的影响。仿真结果表明：大挠性空间桁架的振动频率低,且分布较密;顶端质量块对结构振动频率影响较大,大挠性空间桁架结构受脉冲或周期激励引起振动,仅依靠自身阻尼衰减不明显,且高阶振动衰减速度较低阶衰减速度快;拉索式桁架结构中对角弦张力对整体结构的自由振动频率影响较大,且张紧力越大,低阶振动频率越低,近似成线性关系。本文研究模拟的大挠性空间桁架结构在外太空工作的真实工况,对后续大挠性空间桁架结构的振动控制试验研究有一定的参考意义。

[1]UMLAND J W,EISENT H.SRTM on-orbit structural dynamics[R].AIAA,2001-1588.

[2]BOWDEN M,BENTON M.Design of deployabletruss masts for space station[R].AIAA,1993-0975.

[3]SUTTER T R,BUSH H G.A comparison of two trusses for the space station structure[R].NASA Technical Memorandum,4093.

[4]MAT DA RUS I Z,TOKHI M O.Sof t computingbased active vibration control of a flexible structure[J].Engineering Applications of Artificial Intelligence,2005,18(1)：93-114.

[5]KATTAN P L.Matlab有限元分析与应用[M].北京：清华大学出版社,2004.

[6]李东旭.高等结构动力学[M].长沙：国防科技大学出版社,1997.