一种新的用于反射面天线辐射远场分析的快速积分方法

谢苏隆,钟 鹰

(中国空间技术研究院西安分院,陕西 西安 710000)

0 引言

赋形反射面天线经常通过最优化反射面的形状达到设计目的。当前赋形反射面天线的研究热点是反射面直接展开法[1-5]。这种方法采用如Zernike函数展开式、三角函数展开式、贝塞尔函数展开式、傅里叶级数等一组正交的基函数表示反射面形状。为获得这些基函数的系数,须计算一组观察点的辐射场,并与观察点的辐射场特征相比较,通过优化目标函数取得。在此过程中,需在优化的每个迭代过程中不断重复计算远区辐射场。传统方法是通过物理光学法分析,由计算辐射场积分获得反射面天线的辐射场。计算辐射场积分时,在一定精度要求下,传统积分方法的计算量大、速度慢。为此,本文对一种新的用于反射面天线辐射远场分析的快速积分方法进行了研究。

1 快速积分法

采用本文快速积分法的前提条件是反射面由平缓函数表示,反射面上各点随坐标值变化较缓慢。在实际的赋形反射面天线的设计中,通常反射面由初始偏置抛物面和表示小变形的平缓函数叠加而成。因此,本文的快速积分法的前提条件可以成立。快速积分法步骤如下。

首先分离出反射面上感生电流的相位项,感生电流可表示为平缓函数形式的感生电流的幅值项与变化剧烈的相位项的乘积。

设反射面方程z=f(x,y),反射面上物理光学电流可表示为

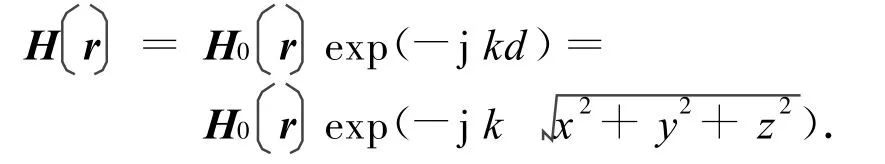
式中：H0(r)为反射面上的入射磁场的幅值;d为从馈源至反射面上某点的距离;j为虚数单位;k为自由空间的波数。则反射面上的感生电流

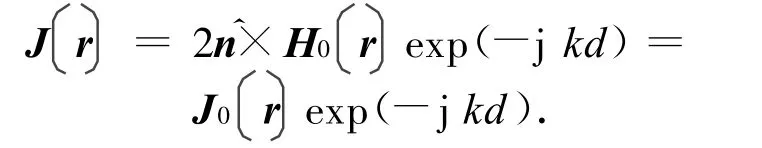
式中：J0(r)为反射面上感生电流的幅值。

其次,给出表示远区辐射场的辐射积分中的相位项。

面电流密度产生的远区场可表示为

式中：Er为远场观察点的电场值;η为自由空间的波阻抗(约377Ω);r′为从馈源到远场观察点的距离;为单位张量;为观察点在极坐标中的单位极径矢量;u=sinθcosφ,v=sinθsinφ,w=cosθ。此处：θ,φ分别为极坐标中远场观察点的俯仰角和方位角。

最后,将辐射场积分在积分域内划分为多个矩形积分网格,在每个矩形积分网格σi内将变化平缓的幅值项由积分网格中心点的值替代、提出,而变化较剧烈的相位项中的相位则通过泰勒展开表示为二次项的形式,在小积分网格内积分,表示为闭合表达式。

积分域内划分为多个矩形积分网格,在每个σi内分别积分,有

式中：S为总网格数。

由于需要积分的网格很小,可认为等效感生电流均布,且等于网格中心点的值,则

设h(x,y)=xu+yv+zw-d,在积分网格的中心点(xi,yi)处作泰勒展开,并略去二阶以上的项,有

令每个积分网格的大小为Δx×Δy,变换积分域,有

因积分网格很小,将exp(j g xy)作泰勒展开,并略去二次以上的高阶项,有exp(j gxy)≈1+j gxy-x2y2,故

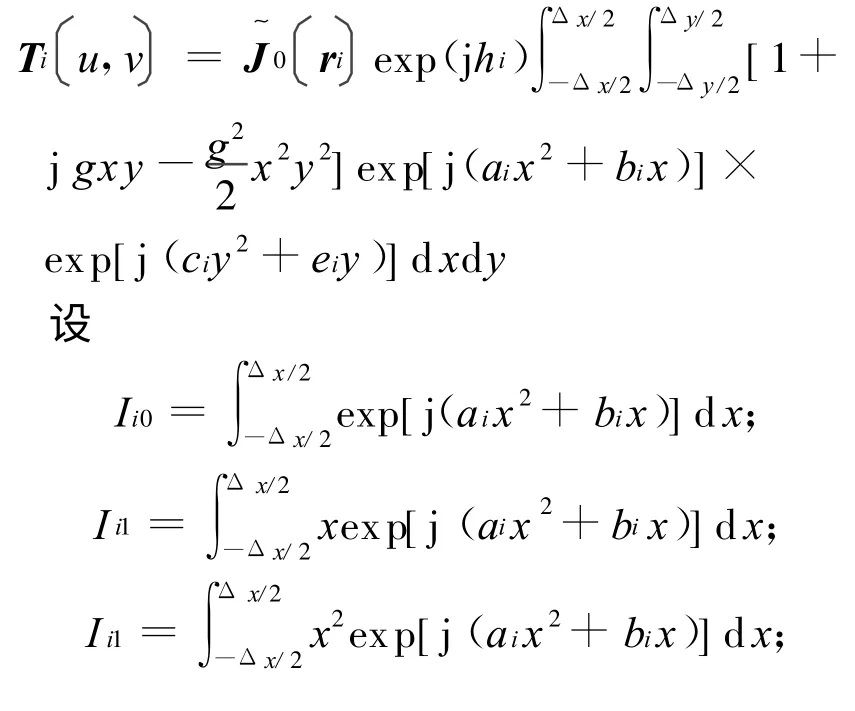
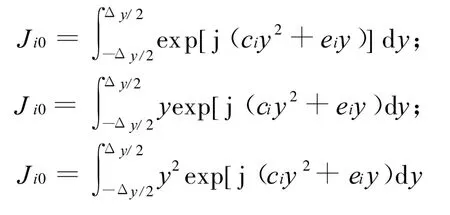
最终得

式中：Ki为积分网格内相位影响辐射场积分的修正项,其值取决于反射面的表达式及其一阶、二阶导数、远场观察点的位置及网格参数(网格大小、网格中心点的位置)等相关项,且

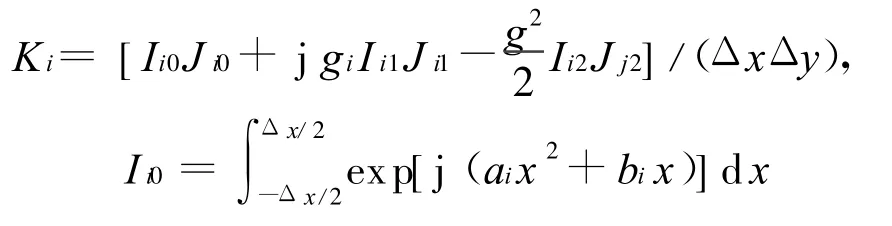
可表示为Fresnel积分形式,或可采用分部积分法推导求解该式的闭合表达式。

2 模拟计算结果

模拟计算中,分别用传统积分方法和本文的新积分方法计算由Zernike函数表示的赋形反射面天线的远场增益值,并比较两种方法的计算性能。

图1 反射面天线结构Fig.1 Structure of reflector antenna

表1 Zernike系数取值Tab.1 Coefficients of the Zernike function

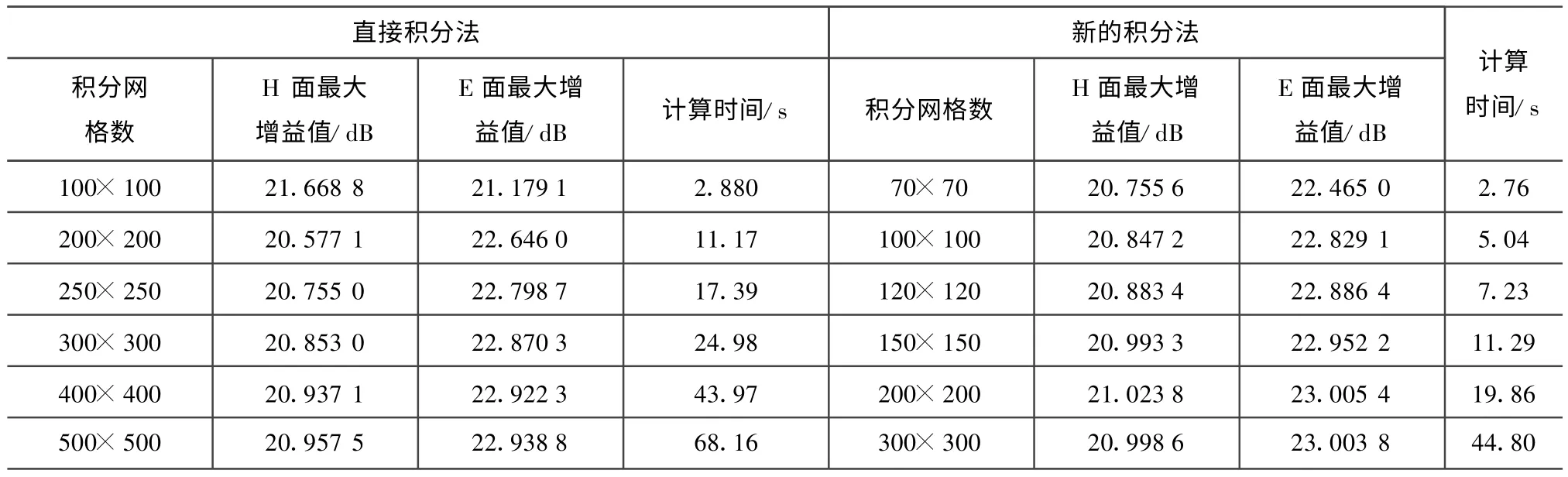
表2 两种方法算得的赋形反射面天线的性能Tab.2 Performances of far field of shaped reflector antenna computed by using two integral algorithms

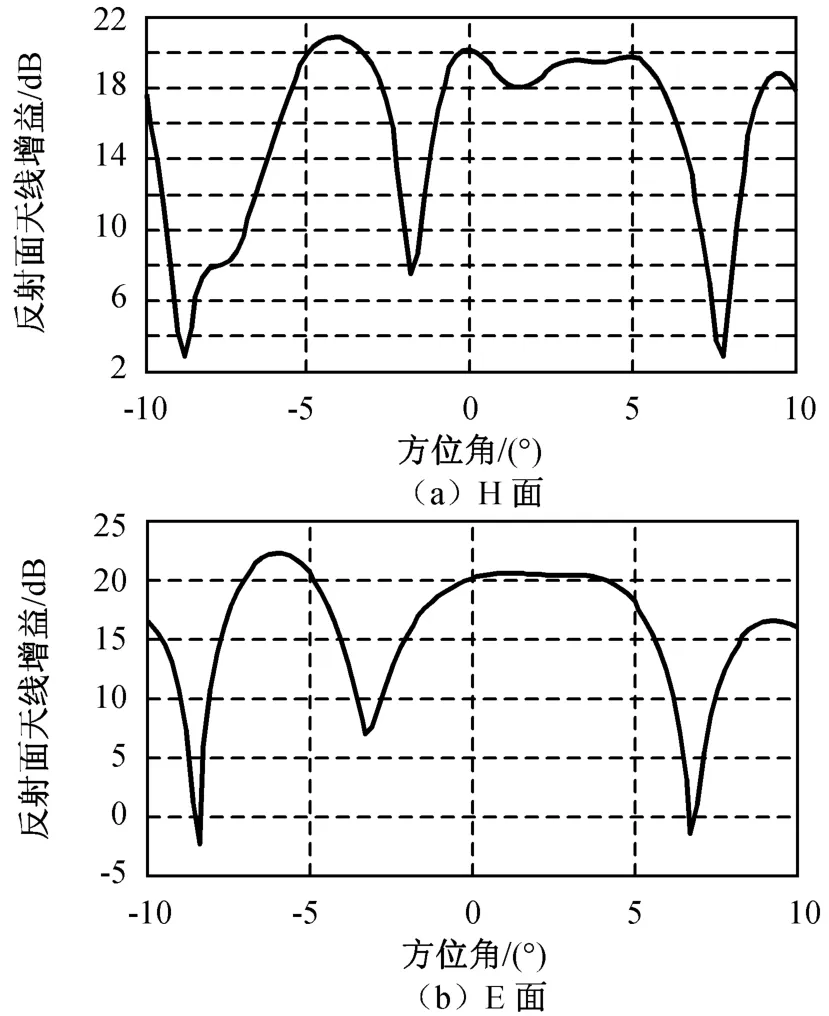
图2 一般积分法计算的的赋形反射面天线远场辐射增益(网格数150×150)Fig.2 Far f ield gain of reflector antenna computed by traditional integral(gird number 150×150)

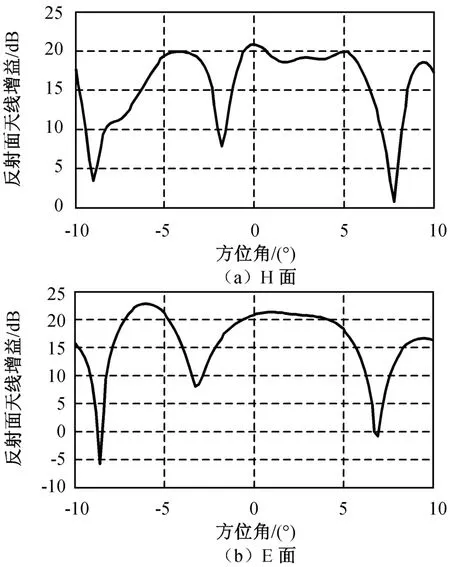
图3 一般积分法计算的赋形反射面天线远场辐射增益(网格数300×300)Fig.3 Far field gain of reflector antenna computed by traditional integral(grid number 300×300)

3 结束语

本文提出了一种新的用于反射面天线辐射远场分析的快速积分法。与传统积分法相比,该方法不再将积分网格内的场值作为固定值,由泰勒展开,计算反射面的表达式及其一阶、二阶导数,考虑积分网格内的相位影响,使在计算精度相同条件下,计算所需的网格的尺寸增大为原网格的2.0～2.5倍,计算所需的网格的数降为原网格的1/4～1/6,所需的计算时间减少为原来的1/4～1/5,从而明显加快了辐射远场的计算速度。此外,由于在每个计算网格内,相位的影响可表示为与网格参数(网格大小、中心点的位置)的闭式,依然可使用如快速傅里叶转换等其他加快计算的近似方法。

图4 新的积分法计算的赋形反射面天线远场辐射增益(网格数120×120)Fig.4 Far f ield gain of reflector antenna computed by new integral(grid number 120×120)

[1]KILIC O,ZAGHLOUL A I,A method for shaped reflector antenna design[C]//Antennas and Propagation Society International Symposium,Clarksburg,M D：IEEE,1998,(2)：836-839.

[2]POULTION G T.Efficient design of shaped reflectors using successive projections[J].Electronic Letters,1991,27(23)：2156-2158.

[3]SEARLEA D.Fast synthesis of shaped reflector antennas,antennas and propagation[C]//The Ninth International Conference on Gec-Marconi Res.Centre UK：[s.n.],1407,1：187-190.

[4]SHOGEN K;NISHIDA H;TOYAMA N.Single shaped reflector antennas for broadcasting satellites[C]//IEEE Transactions on Antennas and Propagation.Tokyo：NHK Science&Technology Research Lab,1992：178-187.

[5]LEE C S.Direct far-field go synthesis of single-reflector antennas using the extrapolation technique[C]//Antennas and Propagation Society International Symposium.Ei Segundo,CA：Hughes Aircraf t Co,1989：Ap-S Digest,3：1162-1165.