天基支援下反导预警时间窗口仿真分析
2012-09-18吕文平李为民
吕文平,李为民,谢 鑫
(空军工程大学导弹学院,陕西 三原 713800)
0 引言
充足的预警时间是反导有效进行的必要前提,能保证反导武器系统有足够的反应时间并最大限度地实现远界拦截。反导预警时间窗口是反应预警时间表征,对该时间窗口的研究是预警时间的组成和关键因素分析的重要内容[1]。
预警系统可分为天基预警系统、空基预警系统和面基预警系统。天基预警的覆盖面广、监视区域大,能尽早发现来袭战术弹道导弹(TBM),对其在反导作战中的应用进行了大量研究。文献[2、3]较系统地分析了国内外天基导弹预警系统,但主要侧重于定性分析。文献[4]对反导作战信息流的时延进行了建模,但主要关注信息流程设计而非预警时间分析。文献[1]对预警时间窗口进行了研究,但预警手段仅考虑了地基雷达,未考虑天基预警卫星的支援。天基支援下反导预警时间窗口是指从天基预警卫星发现来袭的弹道导弹至防御方拦截系统最晚发射拦截弹经历的时间。本文对天基支援下反导预警时间窗口进行了仿真研究。
1 反导预警时间窗口数学描述
根据预警时间窗口的定义,预警时间窗口主要取决于发现目标时刻和拦截系统最晚发射拦截弹时刻。其中,前者主要由天基预警卫星的探测距离、部署位置,以及扫描速率确定,后者则由拦截弹的杀伤区确定。基于天基预警卫星的预警时间窗口如图1所示。图中:t0为TBM的关机点时间;taw为天基预警卫星发现目标时间;tw为拦截弹与TBM最晚遭遇点;tfw为拦截弹最晚发射时间点。
实际反导作战中,反导预警时间窗口取决于攻防双方诸多因素,与TBM目标特性、预警系统预警性能、火力拦截系统战技性能及具体战场环境均相关。
根据拦截弹的运动特性,假设拦截弹到达遭遇点的飞行时间为Δtw,则tfw=tw-Δtw,天基支援下反导预警时间窗口可表示为Tew=[taw,tfw]。

图1 天基支援下反导预警时间窗口Fig.1 Early warning time window with support of space based early warning satellite
2 实体模型
2.1 TBM助推段弹道数学模型
TBM弹道即TBM质心在空间的运动轨迹。在发射坐标系中对TBM助推段弹道进行建模。TBM助推段飞行受力又受控,运动特性较复杂,作用于弹体的力和力矩有发动机推力、控制力和控制力矩、空气动力和空气动力矩、重力,此外还需考虑地球自传引起的牵连惯性力和柯氏惯性力。发射坐标系中TBM助推段质心运动微分方程组(即TBM助推段弹道数学模型)可表示为
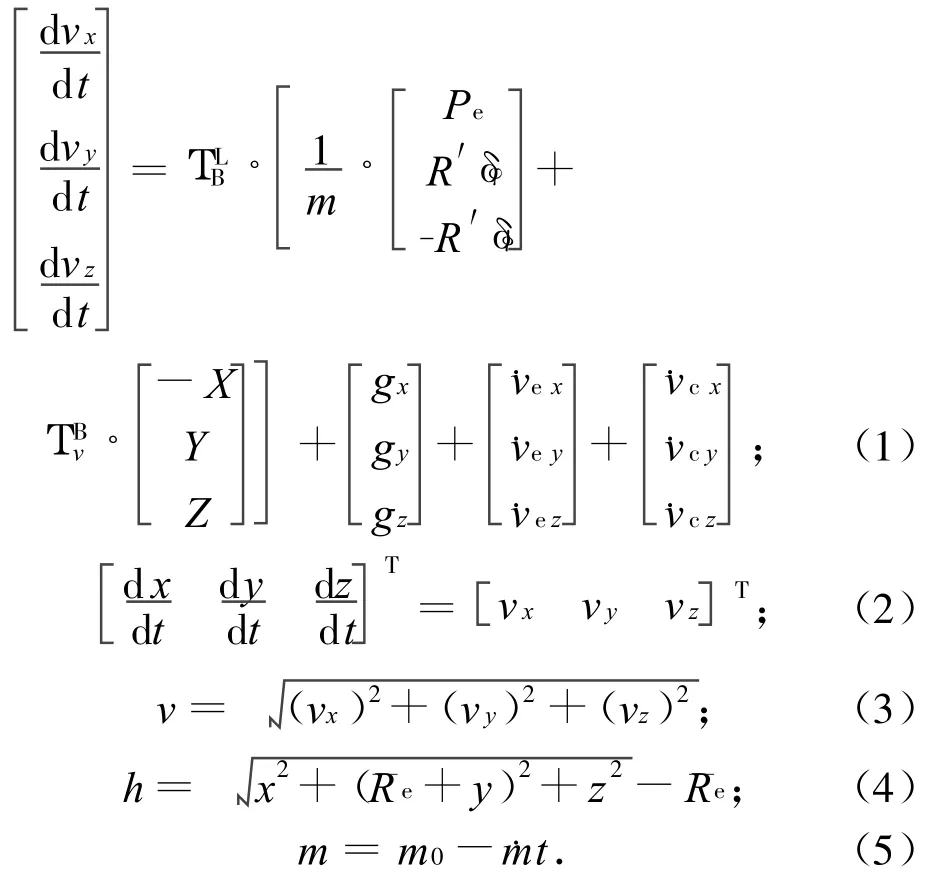
式中:vx,vy,vz为TBM飞行速度矢量v在发射坐标系各轴分量;x,y,z为TBM在发射坐标系中位置坐标;h为TBM飞行高度;为地球平均半径;δφ,δφ为发动机当量摆动俯仰角和偏航角;Pe为发动机有效推力,与TBM弹体纵轴方向一致;R(为一对燃气舵的控制力梯度;m,m0,分别为TBM飞行质量、初始质量和推进剂质量秒流量;gx,gy,gz为重力G在发射坐标系各轴分量;为牵连加速度在发射坐标系各轴分量;为柯氏加速度在发射坐标系各轴分量;为弹体坐标系至发射坐标系的变换阵;为速度坐标系至弹体坐标系的变换阵;X,Y,Z为空气动力R在速度坐标系各轴分量,相应为阻力、升力、侧力[5]。
根据TBM助推段弹道数学模型式(1)~(5),以发射时刻tL为仿真零点,取仿真步长Δt=1 s,发射点大地经纬度取东经0°、北纬20°,大地瞄准方位角45°,则TBM助推段弹道仿真结果如图2、3所示。由图2可知:TBM助推段飞行过程中在ZL轴方向偏移量较小,可近似认为它仅在发射平面XLOLYL内运动。

图2 TBM助推段弹道仿真结果Fig.2 Trajectory simulation of TBM on boosting phase

图3 TBM助推段弹道仿真速度参数Fig.3 Velocity simulation of TBM on boosting phase
2.2 TBM被动段弹道数学模型
可依椭圆导弹理论对TBM被动段进行建模。其要点是由关机点参数构造椭圆弹道计算被动段射程角、射程及飞行时间,并由开普勒方程解算椭圆弹道参数序列,即任意时刻t(tK≤t≤tC)TBM地心距rt、速度vt和俯仰角Θt。TBM被动段弹道数学模型详细解算步骤如下[6]。此处:tK,tC分别为关机点和落点时刻。
a)构造椭圆弹道
设TBM关机点参数为:地心距rK,速度vK,俯仰角ΘK,如图4所示。则椭圆弹道参数半长轴a、半通径p、偏心率e、半短轴b、半焦距c满足

式中:μ为地球引力常数。
b)椭圆弹道参数序列生成
设任意时刻t(tK≤t≤tC)TBM的参数为地心距rt、速度vt、俯仰角Θt。取仿真步长为Δt,则求解椭圆弹道参数序列的方法步骤如下。
步骤a):求解时间参数τ(即过近地点时刻)。由开普勒方程n(t-τ)=E-e sin E,可得
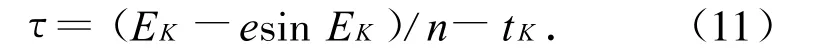
式中:n为平均角速度;E为偏近点角;EK为关机点偏近点角。
步骤b):由开普勒方程采用迭代法,求解时刻t偏近点角Et。时刻t的平近点角


进行迭代计算,直至满足迭代终止条件
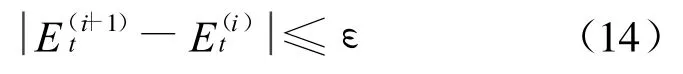
为止。此处:ΔM为中间迭代变量;ε为门限值。则时刻t偏近点角。
步骤c):由Et求解rt,vt,Θt。有

式中:vrt,vft分别为径向与法向速度,且vrt=◦。
步骤d):取推进时间步长t=t+Δt,并判断是否满足终止条件t≥tC,若满足,结束;否则继续步骤b)~d)。
由上述TBM被动段弹道数学模型,对射程1 000 km的TBM,以tk为仿真零点,取仿真步长Δt=1 s,关机点参数为rK=90 000+m;vt=2 437 m/s;Θt=45°,则TBM被动段弹道仿真结果如图5所示。需指出,上述椭圆弹道地心距、速度参数序列是在二维弹道平面解算而得的绝对值,若欲将其表示为参考时刻取关机点时刻tk的地心惯性(ECI)坐标,则还需进行坐标转换。

图5 TBM仿真弹道地心距、速度和俯仰角参数序列Fig.5 Trajectory simulation result of distance to earth center,velocity and up and down angle
2.3 拦截弹弹道模型
根据拦截弹飞行弹道方案,并参考固体火箭弹道设计有关资料,拦截弹飞行助推段的攻角

式中:t1为拦截弹垂直段结束时间;αm为攻角绝对值的最大值;λ为常系数,且2λ=ln 2/(tm-t1);t2为攻角恢复为零的时刻;tk为发动机关机时刻[7]。
建立拦截弹的弹道模型时,按理想弹道模型进行计算,即不考虑地球扁率、大气和控制系统等的影响。拦截弹的弹道模型可表示为

式中:φpτ(t)为俯仰角;θ为速度方向与发射点水平线的夹角;η为极坐标角;α(t)为攻角;g为当地的重力加速度;g0为海平面重力加速度;Re为地球半径;h为拦截弹的飞行高度;m(t)为TBM飞行质量;P(t)为发动机推力;vgx,vgy分别为拦截弹在x、y向的速度分量;xg,yg分别为拦截弹在x、y向的坐标值;CD为阻力系数;ρ为空气密度;为升力系数;S为导弹横截面积[8]。
为保证在拦截不同斜距或不同高度目标时的计算可靠实时,可采用分段形式描述的拟合公式形式,给出拦截导弹飞至不同斜距及高度时的运动学特性,即以导弹飞至不同斜距R和高度H为参数,给出它所对应的平均速度

3 预警时间窗口计算模型
由预警时间窗口的数学描述可知,预警时间窗口的求解需获知参数taw,tfw。计算时,不考虑TBM在发射平面内的横向偏移。取初始时刻t0为TBM发射点时刻,计算步长为Δt,则t0及以后各时刻可表示为

式中:k=0,1,2,…,n。
3.1 预警卫星发现目标时间
因采用GEO预警卫星,故可参照美DSP预警卫星工作方式,即星载传感器按一定角速度ωS循环往复地对特定区域进行圆周扫描,即对特定区域中任一TBM可能发射点,预警卫星每隔60/ωSs可扫描1次。由此,假设预警卫星星下点S地心经纬度为αS,δS,TBM可能发射点B地心经纬度为αL,δL;预警卫星从时刻t0,由初始相位以ωS扫描监测TBM可能发射点,如图6所示。

图6 GEO预警卫星对TBM发射点探测Fig.6 Detection of TBM's launch point with using of GEO early warning satellite
图6中,预警卫星初始相位取零相位,即正东。则在任意时刻t,可用

判断GEO预警卫星是否能扫描到发射点B。若由式(32)算得k为一整数,则说明预警卫星在时刻t能扫描到发射点B,否则不能。此处:ΔtB为预警卫星从初始相位(零相位)开始扫描至第一次扫描到发射点B所经历的时间,且

式中:σB为赤道圈与大圆弧SB之间的夹角(即预警卫星扫过的角),且
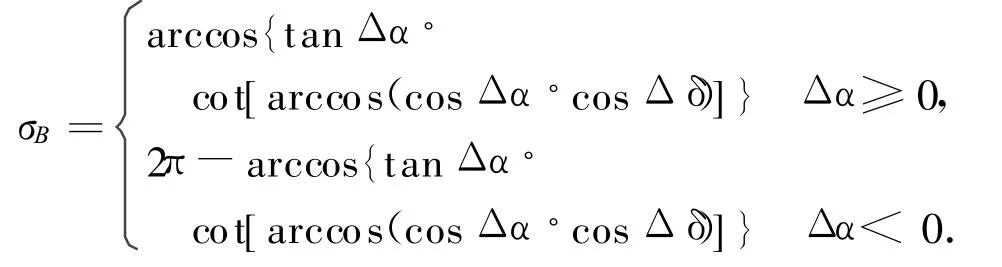
此处:Δα=αL-αS;Δδ=γL-δS。
则可知,若时刻t,TBM可能发射点B恰好发射一枚TBM,则星载传感器通过接收助推TBM火箭发动机喷焰的红外辐射信号,便可探测到该TBM发射。依据仿真需要,对星载传感器探测红外辐射信号进行了简化:即判断TBM红外辐射波长λ是否靠近传感器峰值波长λp,有
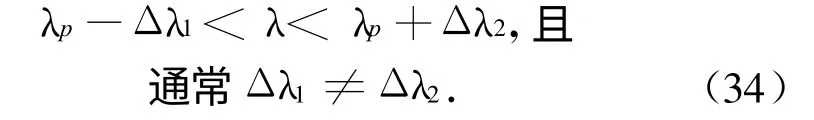
式中:Δλ1,Δλ2分别为传感器在峰值波长λp附近有效敏感的下移波长浮动量和上移波长浮动量,即传感器对波长的敏感范围为(λp-Δλ1,λp+Δλ2)。若式(34)成立,则判断星载传感器能探测到助推段TBM火箭发动机喷焰的红外辐射信号,否则不能。
3.2 拦截弹最晚发射时间
设拦截弹的部署位置在TBM弹道平面上,即拦截弹发射点坐标为(XL,YL),TBM飞行过程中时刻t位置为(XB(t),YB(t))。由杀伤判定原则,拦截弹最晚发射时间与拦截弹的杀伤低界和近界斜距两个战技参数有关。则TBM相对拦截发射点的高度

TBM至拦截弹发射点斜距为

若已知拦截导弹在拦截过程中的速度v(R(t),H(t)),则拦截弹飞至目标时刻t位置所需时间

拦截弹最晚发射时间计算判断准则为R(t)≥Rmin,H(t)≥Hmin。此处:Hmin为拦截弹的杀伤低界;Rmin为拦截弹近界斜距。若上述条件中有任何一个不满足,则最晚早发射时刻计算结束,即

这样,预警时间窗口可表示为

4 算例
设拦截弹战技参数为Hmin=25 km,Rmin=30 km,拦截弹的发射位置部署在TBM落点附近。
当TBM的射程R分别为500,1 000,2 000,3 000 km时,天基预警支援下对不同射程TBM的预警时间窗口进行仿真,结果如图7所示。图中,对天基支援下不同射程的TBM均有较好的预警时间窗口,所得最大预警时间窗口为913 s,基本能满足作战需求。所探测的TBM射程越短,天基支援的效用就越大,主要表现为对TBM初始段的有效预警。本文仿真中,对射程500 km的TBM,天基预警支援下能获得315 s的预警时间窗口,可见天基预警支援作用明显。

图7 不同射程TBM天基支援下反导预警时间窗口仿真结果Fig.7 Simulation result of antimissileearly warning time window for early warning satellite with different firing range TBM as target
为分析天基预警的支援作用,有无天基预警支援时(均有地基远程预警雷达)的预警时间窗口进行了仿真。取TBM射程2 000 km,结果如图8所示。图中:r为地基雷达部署距离。由图可知:地基雷达部署距离越远,天基预警卫星的支援作用则越明显,支援下能获得较地基雷达平均长120 s的预警时间窗口。分析其原因,一是地基远程预警雷达的作用距离有限且受地球曲率和地面障碍物的影响,导致其远程、中远程TBM的初始段探测能力相对较弱;二是因为天基预警卫星凭借其红外探测原理和居高临下的优势,对TBM初始段有较强的探测能力,基本不受TBM射程的影响。
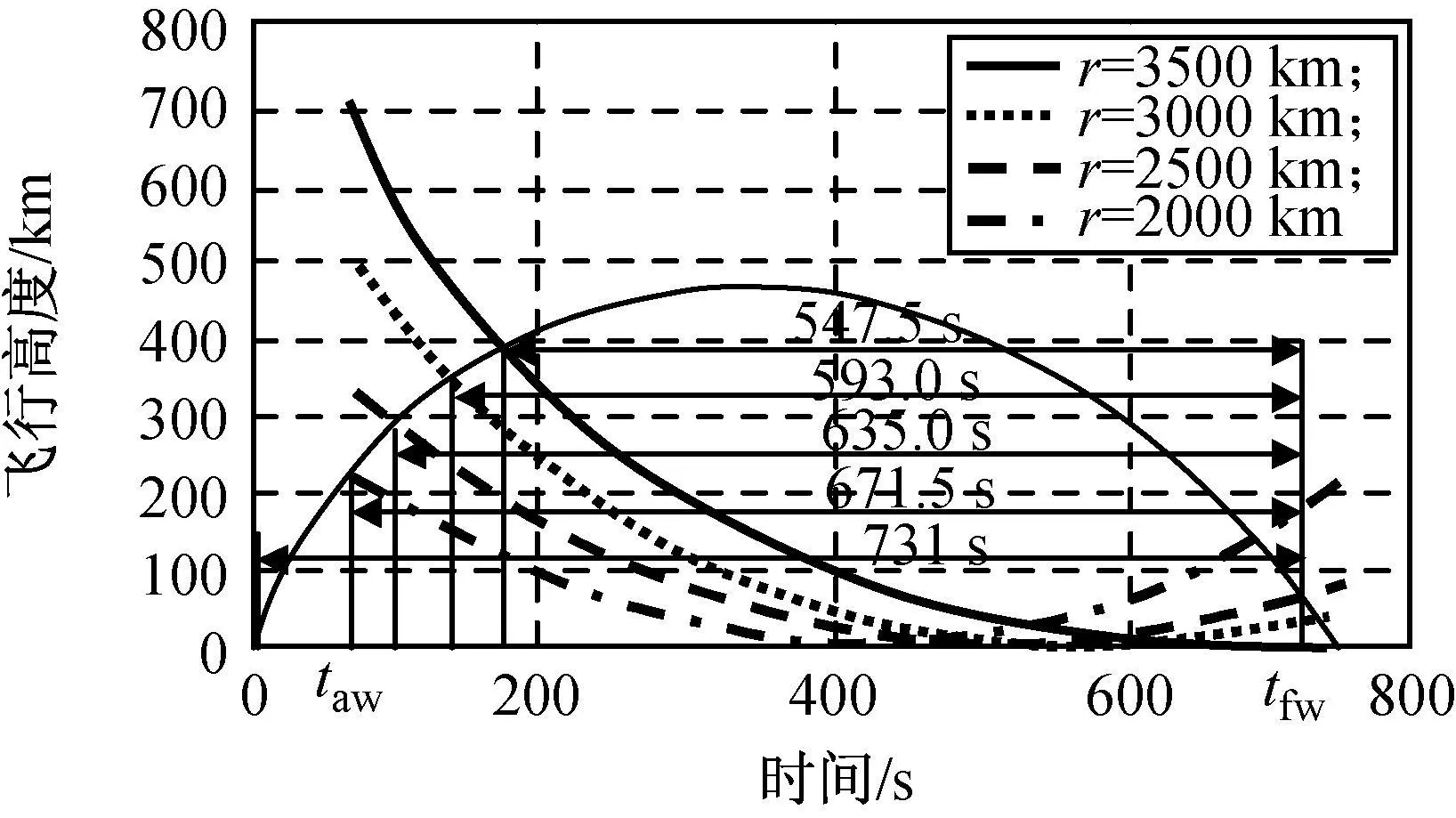
图8 有无天基支援下反导预警时间窗口比较Fig.8 Comparison result antimissile early warning time window between useof early warning and no use satellite
5 结束语
本文对天基支援下反导预警时间窗口进行了仿真分析。结果表明:天基支援能明显扩展反导预警时间窗口;TBM射程越远,天基支援所提供的预警时间窗口扩展净值越大;TBM射程越近,天基支援所提供的预警时间窗口扩展作用反有所增加。
[1]呼 玮,杨建军,龙光正,等.基于地基雷达反导预警时间窗口建模与仿真[J].导弹与航天运载技术,2010(2):51-55.
[2]赵晨光,郑昌文.弹道导弹天基预警与探测手段分析[J].航天电子对抗,2008,24(4):9-11.
[3]王 震,邓大松.俄罗斯天基预警系统浅析[J].电子工程师,2006,32(3):78-80.
[4]曾利新,李为民,王 宏.反导作战信息流时延模型研究[J].现代防御技术,2007,35(1):10-13.
[5]张 毅,杨辉耀,李俊莉.弹道导弹弹道学[M].长沙:国防科技大学出版社,2005.
[6]褚桂柏.航天技术概论[M].北京:中国宇航出版社,2002.
[7]甘楚雄,刘冀湘.弹道导弹与运载火箭总体设计[M].北京:国防工业出版社,1996.
[8]骆文辉.TBM主动段拦截关键问题研究[D].西安:空军工程大学,2008.
