基于纹理的活动轮廓三维图像分割研究
2012-09-18吴琳娜
吴琳娜
(上海宇航系统工程研究所,上海 201108)
0 引言
图像分割是将图像划分为有意义区域的处理技术,它可显著减少随后的图像识别、分析等阶段的数据处理量。因分割中出现的误差会传播到更高层次处理阶段,故其精准度至关重要。图像分割技术在医学诊断及运动分析、结构分析、卫星遥感图像分析等领域有极为广泛的应用。工程中常对图像分割算法有一定的速度要求,并希望减少人工干预,因此图像分割算法的效率和自动化程度同样不可忽略。
目前,常用的三维图像分割算法各有优缺点。如分类器算法是一种监督性算法,具有迭代特点,计算量较小,可用于多通道图像,但需要大量人工干预,算法自动化难度较大;三维边缘检测方法对不同区域对比度强烈的数据分割效果很好,但即使检测出边缘,却很难检测出边缘与感兴趣区域边界的关系;区域增长算法是一种根据预先定义的连接标准从三维图像数据中提取连续区域的技术,算法的实现非常简单,但需要人工交互的选取种子点,对噪声和局部体效应敏感,分割出的区域在空间上离散[1]。针对在噪声较高、待分割的区域的边界和背景区域的对比度非常低条件下分割图像,以快速准确提取感兴趣区域(ROI)的边界、形状和体积等信息,本文对不同分割算法的组合进行了研究。
1 数学模型
文献[2]首次提出了运用活动轮廓模型进行2D图像分割的方法。Snake模型以曲线演化方式实现图像分割。已知三维图像中所有点的灰度值信息,u0(x,y,z)为图像每点(x,y,z)的灰度值。令S为ROI的边界;inside S,outside S分别表示ROI内、外部的点。MUMFORD等提出了能量方程:三维图像在以S为轮廓边界时能量函数可表示为
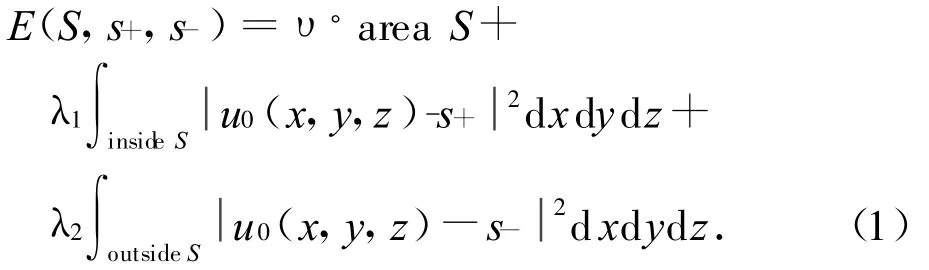
式中:area S为ROI轮廓的表面积;s+,s-分别为ROI内、外部所有体素灰度值的均值,s-即为图像中视作ROI背景所有体素灰度值的均值;υ,λ1,λ2为权重系数[3]。式(1)中,等号右端第二部分是对ROI内部所有点的积分,是ROI内部体素灰度值的方差;第三部分是对ROI外部所有点的积分,是ROI外部体素灰度值的方差。对所分割的图像有如下的先验知识,先收缩ROI的表面积,并尽可能拟合连通的区域;其次,最小化ROI内部和外部体素灰度值的方差之和,使内部和外部的体素灰度值特征尽可能均衡。由此,图像分割转化成能量方程的最小化
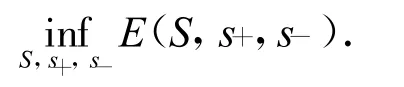
基于以上概念,文献[4]提出了无边缘的活动轮廓法,但在解决本文问题时该经典算法的效果并不理想。实验中发现该算法在一定程度上消除了离散的点和区域,但同时也将部分ROI外的体素划进ROI内部。
为进一步利用图像中除灰度值以外的信息,考虑通过变化提取更多的图像信息(目前能量方程仅包含单通道图像的信息)。GABOR在1946年就提出了Gabor方程,之后DAUGMAN将其推广到了二维[5-6]。本文研究的图像因采集方式的关系,图像ROI区域具备纹理特征。Gabor方程常用于有一定纹理特征的图像[7]。Gabor变换可分割空间频域、元素密度、方向、相位、能量有区别的区域[8]。二维Gabor方程或称Gabor滤波器可表示为

式中:gσ(x,y)=为二维高斯方程;F,θ分别为频率和相位参数,决定了该变换作用的方向。此处:σ2为方差,其值越大,变化影响的邻近区域就越大。u0→(u0)σ,F,θ是空间点u0(x,y,z)在Gabor变换之下的值。该变换的特点是与θ向垂直的边界会被突出,而对所作用的图像来说,变换结果会变得平滑,起到降低噪声和增强局部纹理特征的作用。每选取一个θ对图像进行变化,就能获得图像在一个新通道上的信息。通过N次Gabor变化所得N通道的信息可用能量方程表示为

能,其是满足顾客入住需求的关键。这个过程中酒店人员利用酒店前台管理系统对顾客信息进行录入,客人正式入住后边可通过相应系统为客人做其他需求服务办理。通常酒店前台管理系统本身灵活性也相对较高,比如其在权限操作上,不同管理人员所具有的操作权限也有一定差异性。结合实际来看当前酒店前台管理系统服务需求主要体现在房间预订、登记入住、换房、加房、修改房价等特性,注重前台管理系统完善性和功能要点的灵活设置,是整个酒店管理系统得以流畅运行的关键[1]。
分别为图像在第i个通道ROI内、外部变换值的均值;s0+,s0-分别为ROI内、外部在每个通道上变换值均值的向量,且,S更新时两组向量值将重新计算;λi,γi为权重系数,取值源于实验或经验数据。当υ的取值固定后,对比实验结果选取合适的λi,γi值。
为表示轮廓S,本文引入水平集方程。水平集无显式的定义边界,仅规定边界上的值φ(x,y,z)=0,ROI内部φ(x,y,z)>0,而外部取负值。最简单的度量水平集的函数是Dirac方程,inside S取值为1,outside S取值为0。BAYER研究了多种近似Dirac方程的方法[9]。本文采用其中正则化的Heaviside函数:H2,ε(z)=,δ2,ε(z)=H′2,ε(z)=拟合Dirac方程的δ函数表达。此处:ε为当z在0附近时H2,ε(z)的斜度。
为优化能量模型并简化计算,本文引入统计模型。以2D图像为例,作如下假设:
a)轮廓(分割边界)的长度与其成为边界的概率满足关系p(P(Ω))∝e-υ|C|,υ>0。此处:|C|为轮廓的长度,即轮廓Ω越短,成为图像边界的概率越大。
b)无关分布,最大后验概率(MAP)可表示为

式中:I为待分割图像的已知信息。
c)ROI内、外部的像素灰度值均满足正态分布,如图1所示。两部分灰度值均值接近,且灰度值的取值范围有重叠,但各自满足正态分布。
对式(4)求负对数。令E(Ω)=-lg(p(P(Ω)|I)),Ω1为inside S的区域,Ω2为outside S,则有
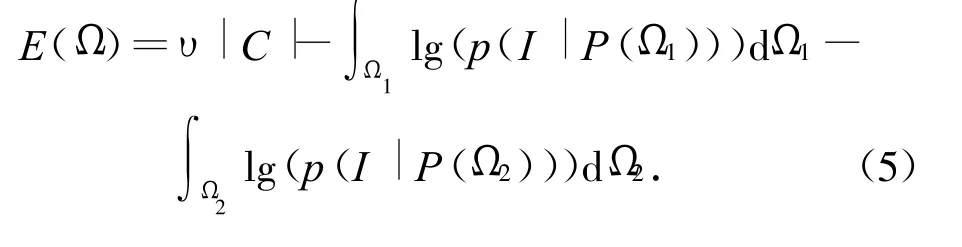

图1 ROI内外灰度取值分布Fig.1 Distribution of gray valueinside/outside ROI
基于这些概率假设,最大化p(P(Ω)|I)和最小化E(Ω)等价。可发现此处E(Ω)也可视作2D图像能量方程的表示。这些假设和推导对三维图像同样有效。对三维图像的能量方程,综合概率统计的模型和水平集的表达式为
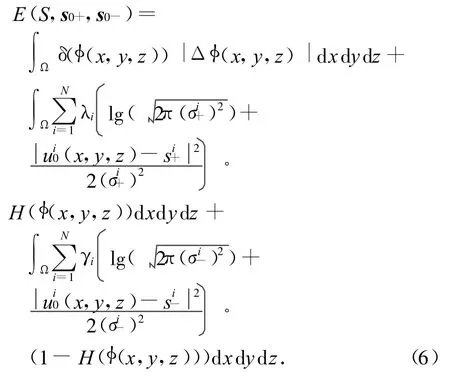
式中:

此处:φ为水平集函数,定义了点(x,y,z)所处的区域;H(φ(x,y,z))为水平集函数的正则化表达,取值为(0,1),以免数值范围过大;δ(φ(x,y,z))为H(φ(x,y,z))的导数。
2 数值计算
2.1 算法性能
三维图像处理中,须考虑数值计算量。图像大小1 024×1 024×1 024时,点的存储空间可达GB级别的存储量,在确保不丢失ROI信息的前提下,应采用预提取或重新采样法减小图像尺寸。水平集已广泛用于描述轮廓和分割物体中,但由于其计算的复杂度与图像的体素成正比,而普通的水平集法是用尺寸固定的网格点计算未知点,用偏微分方程推进水平集的移动,导致迭代周期过长。
ADALSTEINSSON提出了窄带技术以加快水平集方程的移动速度,大幅降低额外的计算开销,进而提高算法的效率[10]。方法要点是考虑将轮廓在一定距离范围内的体素点看作一个带状,如图2所示。在每步迭代中,窄带会由最新的轮廓重新计算而得。SETHIAN提出了快速步进法计算距离[11]。该法的要点是在零水平集中建立可适应的网格。
图2仅考虑零水平集的在管道内部邻近点,计算复杂度从O(n3)降至O(n2)。此处:n为图像在一个维度上的点数。同样,对内存的需求也由三阶降为二阶。窄带方法的缺点是,管道永远不能覆盖整个图像区域。对管道,初始化方法有多种,最简单的是将图像中心作为球心,以指定长度为半径画出球形作为初始管道,如半值过大会导致计算量增加,半径过小又会导致管道与ROI无交集,从而混淆ROI的内部和外部。另外引进重新计算距离技术,可避免水平集方程演进过程中因过于平坦而粘滞在局部区域。

图2 不使用和使用窄带的水平集Fig.2 Level Set without/with narrow band
2.2 收敛条件
通常,偏微分方程求解采用标准的半隐式方法和AOS方法。AOS特点是:适于并行计算,可直接推导到更高阶的问题无需修改算法的结构。WEICKERT等证明了AOS法效率较显式方法高10倍[12]。对实时性能要求,必须为算法收敛性和收敛速度考虑合理的收敛条件。CHEN-VESE给出的收敛条件是在管道内,点的水平集的变化绝对值均值小于某收敛值,即轮廓在迭代中“几乎”不再移动时算法收敛,此时能量方程也趋于稳定。同时还会设定一个固定的最大迭代次数值以控制迭代次数。
2.3 计算步骤
求解水平集的数值实现是基于对偏微分方程的有限差分逼近。通过改变水平集方程来驱动轮廓的运动。其步骤如下:
步骤a)由于窄带方法假设管道边界上的网格点和管道邻近点有相同的符号,每次迭代前边界上的值均需重新初始化。
步骤b)每次迭代中,重新计算每个通道的水平集统计信息。
步骤c)用新的水平集统计信息值更新水平集的力场值,对应偏微分方程用向前欧拉步进法更新。平均曲率的运动用加性分裂算子(AOS)逼近。
步骤d)重新计算水平集距离,更新窄带。
步骤e)在下次迭代开始前,根据收敛条件判断循环是否停止。
3 实验结果及分析
实验取4个方向作为Gabor变换的方向,均位于与Z轴垂直的平面中,θ的取值为0,,即N=4。设4个通道Gabor变换的权重参数为λi==200,i=0,1,2,3。通过对一组数据进行20组实验,选取不同的λ值,对比实验结果的误差,发现当λ=800时,分割误差值最小。在15组三维图像的数据的分割运算中,平均在20次迭代之内,算法就能达到收敛,平均运算时间小于5 s,应用中能实现快速分割。
用户用工具手动画出的轮廓如图3(a)所示,本文算法提取的图像如图3(b)所示。用HUTTENLOCHER的Hausdorff距离判别两条轮廓曲线的误差。其中,15组数据的分割图像结果的Hausdorff距离平均值为0.966 5,表明算法提取的轮廓与验证结果的像素偏离很小,准确度达到期望结果。

图3 三维图像分割结果的一个二维截面Fig.3 2D section from 3D segmentation results
4 结束语
本文根据常用三维图像分割算法,提出了综合图像纹理和统计学信息的活动轮廓算法,并进行了实验验证。算法的重点是纹理提取变换在多通道中的合成,可提供较原始图像更完整的分割信息;水平集方法克服了参数化表示轮廓的缺陷,半隐式的数值算法可显著加大每次迭代的步长,加快收敛速度,收敛准则在迭代趋于稳定时轮廓移动较小,可减少总迭代次数。在三维活动轮廓模型采用了Gabor变换,算法在效率和准确度均达到实用要求。算法的缺陷是不同采集方式获得的图像的λ取值并不确定,故还需研究不同类型图像的不同收敛性和精确度的λ值确定方法。后续研究还可包括知识库建立,以及典型图像特征求解及系列参数值存贮。
[1]LI S Z,Markov random field modeling in computer vision[M].Tokyo:Springer-Verlag,1995.
[2]MUMFORD D,SHAH J,Optimal approximations by piecewise smooth functions and associated variational problems[R].Center for Intelligent Control Systems,1988.
[3]CHAN T F,VESE L A.Active contours without edges[J].Image Processing,IEEE Transactions on,2001,10(2):266-277.
[4]DAUGMAN JG.Uncertainty relation for resolution in space,spatial f requency,and orientation optimized by two-dimensional visual cortical filters[J].Optical Society of America,Journal,A:Optics and Image Science,1985(2):1160-1169.
[5]SANDBERG B,CHAN T,VESE L.A level-set and Gabor-based active contour algorithm or segmenting textured images[R].UCLA Department of Mathematics CAM Report,2002:02-39.
[6]CLARK M,BOVIK A C,GEISLER W S.Texture segmentation using Gabor modulation/demodulation[J].Pattern Recognition Letters,1987,6(4):261-267.
[7]BEYER R P,LEVEQUE R J.Analysis of a one-dimentional model for the immersed boundary method[J].SIAM J Number Anal,1992,29(2):332-364.
[8]ADALSTEINSSON D.A fast level set method for propagating interfaces[D].Oakland:University of California,1994.
[9]SETHIAN J A.Level set methods and fast marching methods[J].Computer Vision and Materials Science,Cambridge University Press,1999.
[10]WEICKERT J,ROMENY B,VIERGEVER M A.Efficient and reliable schemes for nonlinear diffusion filtering[J].IEEE Transactions on Image Processing,1998,7(3):398-410.
[11]HUTTENLOCHER D P,KLANDERMAN G A,RUCK LIDGE W J.Comparing images using the Hausdorff distance[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1993,15(9):850-863.
[12]CHEN Y,TAGARE H D,THIRUVENKADAM S,et al.Using prior shapes in geometric active contours in a variational framework[J].International Journal of Computer Vision,2002,50(3):315-328.
