水库诱发地震震级预测的统计研究＊

王 博蒋海昆 宋 金

（中国北京100045中国地震台网中心）

水库诱发地震震级预测的统计研究＊

（中国北京100045中国地震台网中心）

基于收集到的全球102例水库及已发地震的资料，应用隶属函数方法综合分析了水库基本属性、震中区岩性、库坝区基本烈度和震中区断层类型等与水库诱发地震之间的关系，从统计学角度给出了水库诱发最大地震震级的判定方法.通过回溯检验和费舍尔判别检验给出了预测震级的相对误差和正确识别率，总体预测效果较好，可为将来水库的设防和最大地震震级的判定提供统计学上的依据.

水库诱发地震 震级预测 隶属函数 费舍尔判别

Abstract：Based on the collected data of 102 global reservoir－induced earthquakes and by using the method of membership function analysis，we comprehensively analyzed the relationship between reservoir－induced earthquakes and basic properties of the reservoir，lithology of the epicentral region，basic seismic intensity in the reservoir region and fault types of the epicentral region.From a statistical point of view，a method of predicting the maximum magnitude of reservoir－induced earthquakes is proposed.Through the Fisher discriminant analysis and a retrospective test，the relative error of the predicted magnitude and correct recognition ratio are given.The overall prediction result is rather satisfactory and can provide a statistical basis for reservoir seismic fortification and judgment of the possible maximum earthquake magnitude in the future.

Key words：reservoir－induced seismicity；magnitude prediction；membership function；Fisher discriminant

引言

自1931年希腊马拉松（Marathon）水库首次发生地震以来，水库诱发地震的研究已有近80年的历史，对水库诱发地震震级的推算也有很多报道（Baecher，Keeney，1982；常宝琦，梁纪彬，1987；李安然等，1992；李华晔，1999；Gupta，2002；闫雪莲等，2009；张飞宇等，2009；王晓青等，2009）.上述方法都从不同角度给出了预测水库诱发地震最大震级的判定方法，但构造型水库地震的发生是多因素相互作用的结果.在多个因素的综合作用过程中，每个因素作用方式的贡献并不明确，加之目前水库诱发地震总数并不多，所以每种方法都存在一定的不确定性.

常宝琦和梁纪彬（1987）曾明确指出，决定水库诱发地震最大震级的不只一个参数，随着其它合理参数的进入，水库诱发地震最大震级的预测估计会有进一步改善.综观前人研究，多数作者认为高坝大库诱发几率高，反之则低.其实无法找到理想的对应关系，更未见到准确的数学模型，这种笼统的提法掩盖了其它因子的综合效应，不利于揭示诱震机制.所以，在水库基本属性与震级关系初步研究的基础上，通过找出尽可能多的对水库诱发地震有影响的因子，对水库诱发地震进行多影响因素的综合分析，对水库诱发地震最大震级进行统计研究，这对新建水库的抗震设防以及已建水库的运行安全等都具有较重要意义.

1 资料和方法概况

本文共收集到全球102例M≥1.0水库诱发地震资料.依据收集到资料的完整情况，在总结前人研究成果的基础上，选取库容、库深、震区岩性、构造活动（基本烈度）和区域应力状况（断层类型）等5个因素，通过构建单因素对水库诱发地震的隶属函数，定量刻画出每个因素对水库发震的贡献大小，根据每个因素在水库诱发地震中的地位及作用的最大程度确定其权重，选取其权重的集合为A＝｛0.4，0.6，1.0，1.0，1.0｝.然后，扣除所有对诱发地震不利的情况.其数学模型为

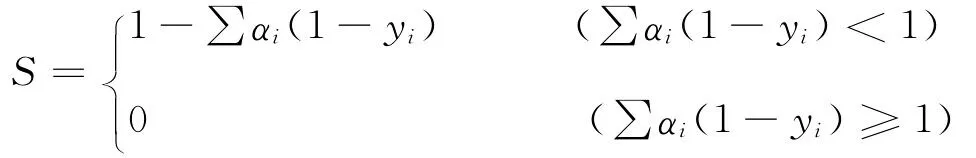
式中，S为综合评分，表示孕震强度或孕震能力大小，与水库最大震级M相关；yi为各影响因素对孕震强度的隶属函数；αi为各影响因素的权重.由上述隶属函数及每个因素的权重，决定其综合评分值.震级M与综合评分值S的关系为M＝10S.

2 数据处理与分析

水库诱发地震由于成因上的特殊性，在其分布、孕育和发生的过程等方面均不同于天然地震，更多地与所处地质构造和水库蓄水量及蓄水过程密切相关（丁原章，1989）.一般而言，库容大的水库诱发地震活动的可能性大于小库容的水库，但它们诱发的震级有大有小.同样，小库容水库也会诱发地震，尽管比例相对较小，并且小库容水库诱发地震的震级同样是有大有小（Baecher，Keeney，1982；光耀华，1988；Gupta，2002；乔东玉等，2008）.图1为水库诱发地震的最大震级与库容对数的散点图，可见两者没有显著相关性，也不存在简单的线性关系，这同时也说明了震级不是由库容一个因素所能决定的.虽然如此，库容越大，受水体作用的岩体体积及面积增大，遇到有利于发震的地质条件的概率就越高，其水体在孕震中的贡献相对增大，隶属函数值增大，但震级不一定很高.反之，库容越小，水体在孕震中的贡献相对减小，隶属函数值也相应减小.依据此情况，对库容与震级进行非线性曲线拟合，求出库容对震级的隶属函数y1＝v/（v＋1）（王石青等，2002；乔东玉等，2008），计算库容对诱发地震的贡献度大小（图2）.

基于坝高与库深有较好的联系，本文收集到的库深数据较多，故采用正常蓄水时的库深数据.一般来说，大坝越高，库水越深，库区岩体中孔隙水压力增加越大，作用在断裂面上的有效应力和沿断裂面的抗剪强度则降低越多，诱发地震的可能性增大，其贡献也相对增大；反之，大坝越低，诱发地震的可能性就减小，其贡献度也相对减小.同样，求出库深对震级的隶属函数y2＝1－15/（H＋14）（王石青等，2002；乔东玉等，2008），计算库深对诱发地震的贡献度大小（图3、图4）.

岩性也是断层渗漏、水库诱发地震的影响因素之一.一般来说，岩石密度愈大，其强度也愈大；孔隙度愈大，则密度愈小，强度愈低.从诱发地震的坝址岩性来看，这些岩石密度大致在2.3—2.9 g/cm3，只是处于中等硬度.除此之外，流体长时间浸泡也会导致岩石抗压强度的降低.据刘佑荣和唐辉明（2006）研究结果，不同岩性抗压强度在湿样条件下降低程度不同，页岩和黏土岩减少幅度较大，石英岩、玄武岩和花岗岩降低的幅度相对来说较小，但每种岩石的软化系数也随着外界条件的改变而大小不同.由于不能给出每类岩性的隶属度大小，故依据乔东玉等（2008）经验，本文仅按沉积岩、火成岩、变质岩三大成因类型的岩石，分3类粗略给出其隶属度分别为0.89，0.96和0.87.

构造活动与水库诱发地震亦有一定联系，构造活动历史最直观的表现即是历史地震活动.因而，一个地区较高的地震烈度，往往意味着该区域构造活动相对强烈.基于已有的烈度－震级经验统计关系（国家地震局震害防御司，1992），给出线性拟合公式I＝1.666 7 M－2.166 7，利用水库周围50km范围内历史上曾发生过的最大地震震级来粗略估算该区域的基本烈度，然后再求取烈度的隶属函数y3＝1－250/（I4＋350）（王石青等，2002；乔东玉等，2008），计算库坝区基本烈度对诱发地震贡献度的大小（图5）.

由于已有统计公式基本上依据较高震级（至少有感）地震数据得到，对小地震并不适用，因而对2.0级以下地震，此处粗略地取烈度为1.

区域应力状况也是影响水库发震的一个重要因素.按照以往的研究，库水渗透对正断层影响最大，对逆断层影响最小.这里采用简单的分类方法，按正断层、走滑断层和逆断层3种类型，分别赋以隶属函数值为0.97，0.92和0.68.遇到张扭性和压扭性等断层时，按两者的实际情况确定.由于缺乏水库发震断层的基础资料，本文在统计分析过程中，将3种类型分别进行了计算，取计算震级最接近实发震级的断层性质作为水库发震断层的类型.

图5 库坝区基本烈度（I）－隶属函数y3曲线图Fig.5 The membership function（y3）of basic seismic intensity（I）in reservoir and dam areas

3 讨论与结论

对有上述5项基本属性资料的102个M≥1.0震例进行了计算，并进行回朔分析，结果如表1所示.其中，有23例无法计算出合理的结果.从能够给出计算结果的79例震例中，以预测震级Mp与实际最大震级Ma的相对误差［（Mp－Ma）/Mp×100%］表征其预测精度，平均来看，当预测震级介于1—1.9，2—2.9，3—3.9，4—4.9及5级以上时，预测结果与实际最大震级相对误差绝对值的平均值分别为257.2%，59.7%，18.0%，2.3%及13.6%.可见对震级较小的水库诱发地震预测结果与实际偏差较大，震级较大地震的预测结果与实际相对较为接近，当预测震级大于3级时，预测偏差尚可接受.例如，当预测震级Mp介于4—4.9范围时，实际震级Ma＝Mp（1±2.3%）；当预测震级Mp≥5.0时，实际震级Ma＝Mp（1±13.6%）.在50例Mp≥3.0震例中，相对误差绝对值小于10%的有25例，占3级以上地震震例的50%；相对误差绝对值小于20%的有47例，占3级以上地震震例的94%.

表1 水库诱发地震最大震级的多因素综合预测Table 1 Predicted result of the maximum magnitude of RIS by multi－factor analysis

续表1

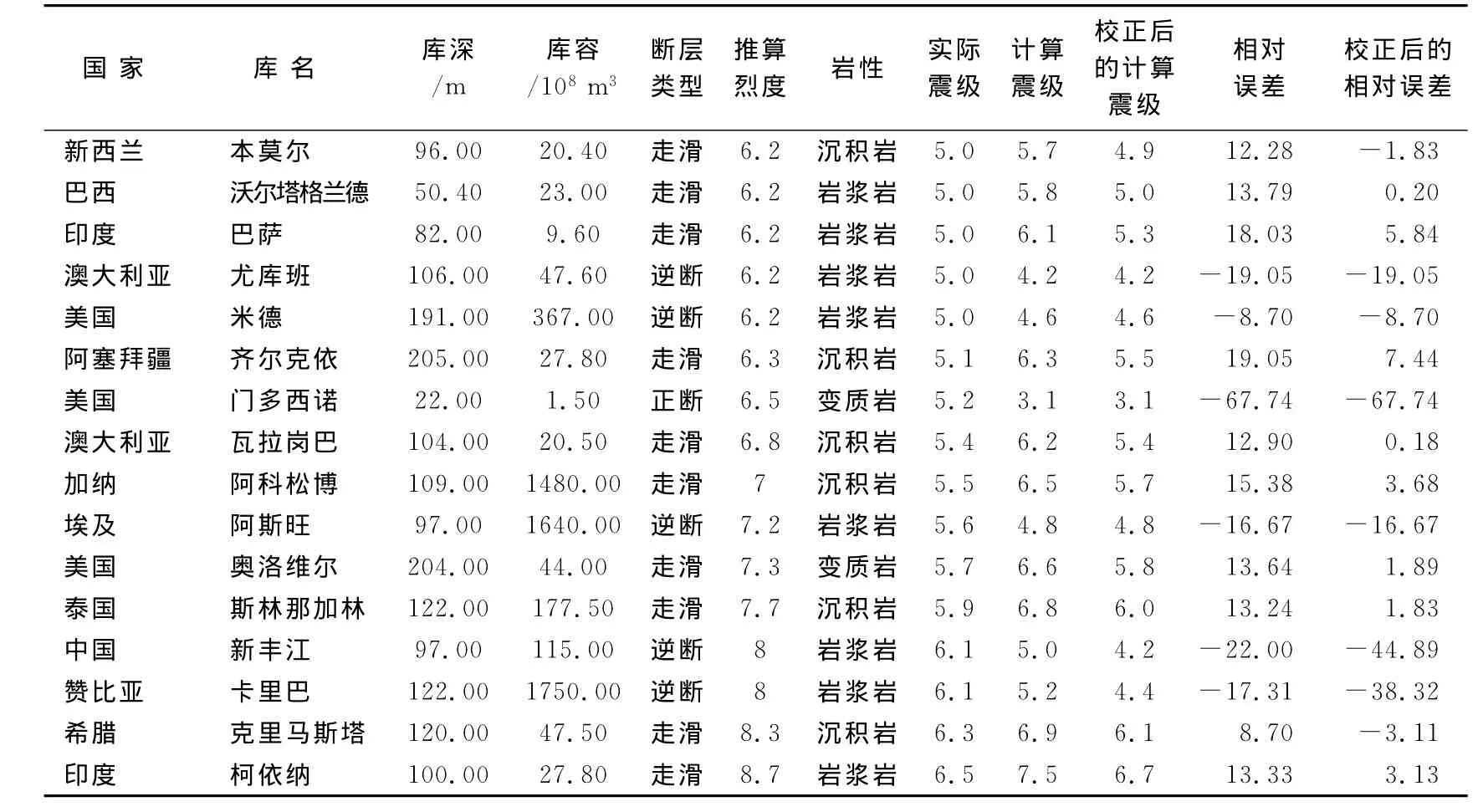
续表1

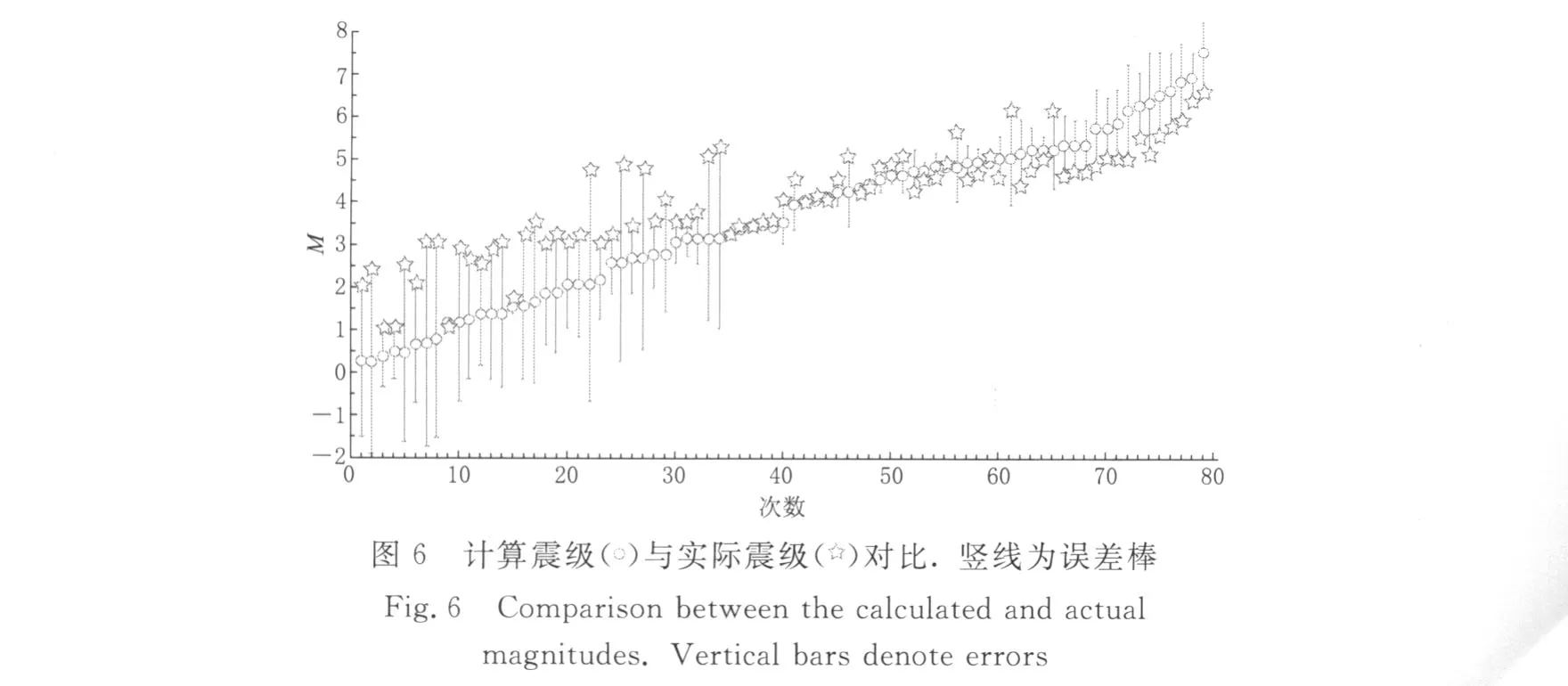
图6给出了79例震例计算震级与实际震级的对比，图中误差棒表示计算震级与实际震级之间的相对误差范围.可见当预测震级小于3级时，预测结果系统偏低，平均偏低约1.39级；当预测震级大体上介于3—5级范围时，预测结果与实际较为吻合，平均偏差约为0.42级；当预测结果大于5级时，预测结果系统偏高，大约平均偏高0.79级.据此可对预测结果进行粗略校正，将不同震级范围内的计算震级根据与实际震级的平均偏差进行相应的增大或者减小，即，当Mp3.0时将预测震级Mp增加1.39，当Mp＞5.0时令预测震级减小0.79，结果如图7所示.经校正的预测结果与实际震级更为接近，当初始预测震级Mp3.0，3.0＜Mp5.0和Mp＞5.0时，经校正后结果的平均相对误差绝对值分别为21.6%，11.1%和5.4%.

为了进一步检验计算震级与实发震级的相关性，对基于上述73例实发震级大于等于3级的地震，将水库库深、库容、库区岩性、库区基本烈度及断层属性等5个因素的隶属函数作为自变量，依据实际最大震级分为M≥4.5和M＜4.5两类，采用两类等权的方式建立判别函数，对最大地震震级的分布区间进行费舍尔判别.

YM≥4.5＝－1 125－28.534×库容隶属函数＋305.422×库深隶属函数＋100.513×烈度隶属函数＋1 449×岩性隶属函数＋679.504×断层隶属函数

YM＜4.5＝－1 123－30.867×库容隶属函数＋301.935×库深隶属函数＋140.920×烈度隶属函数＋1 433×岩性隶属函数＋668.085×断层隶属函数

回顾性检验结果显示，对37例M≥4.5的地震，识别正确率为100%；对36例M＜4.5的地震，有31例识别正确，识别正确率为86%，有5例（14%）被误判为4.5级以上，整体判别效果较好.

本文给出了水库基本属性、震中区岩性、库坝区基本烈度以及震中区断层类型等与水库诱发地震之间的关系，应用隶属函数方法给出了水库诱发最大地震震级的判定方法.回溯检验和费舍尔判别检验结果显示，预测震级的相对误差较小，总体正确识别率较高，预测效果较好，从统计学的角度为将来水库的设防和最大诱发地震震级的预测提供了方法和判定依据.

关于水库地震，一直有水库诱发地震和水库触发地震两种说法（陈厚群等，2009）.虽然两者的地震成因有所区别，需从水库所处的地质构造条件进行分析，但鉴于目前对这两种说法没有达成较好的共识，总的水库地震数量也较少，且绝大多数属于非构造型地震，故文中统称为水库诱发地震.本文选取的因素虽然在水库诱发地震中都起到一定的作用，但还有其它一些因素（如区域应力状态、库水位变化等）在水库诱发地震中也有较强的作用.限于统计资料的不完整和量化的困难性，仅从已有资料给出的水库最大震级和水库基本属性的统计公式，仍然存在适用上的局限性，需在今后的工作中确定更多的影响因素及做更进一步的研究.

常宝琦，梁纪彬.1987.水库“规模”与水库地震震级的关系［J］.华南地震，7（1）：94－－99.

陈厚群，徐泽平，李敏.2009.关于高坝大库与水库地震的问题［J］.水力发电学报，28（5）：1－－7.

丁原章.1989.中国的水库诱发地震［J］.华南地震，9（1）：64－－72.

光耀华.1988.论水库要素与水库地震的关系［J］.四川水力发电，（4）：28－－33.

国家地震局震害防御司.1992.地震工作手册［M］.北京：地震出版社：316－－318.

李安然，张飞飞，张珂.1992.从新丰江水库地震的环境条件讨论水诱发地震的研究及其预测［J］.华南地震，12（3）：88－－94.

李华晔.1999.水库诱发地震研究（二）［J］.华北水利水电学院学报，20（2）：24－－29.

刘佑荣，唐辉明.2006.岩体力学［M］.北京：中国地质大学出版社：32－－36.

乔东玉，高志飞，洪迎东，韩治国.2008.应用数学模型对构造型水库诱发地震震级进行预测的探讨［J］.水利水电工程设计，27（4）：34－－38.

王石青，邱林，王志良，韩晓军.2002.确定隶属函数的统计分析法［J］.华北水利水电学院学报，23（1）：68－－71.

王晓青，丁香，张飞宇，郑友华.2009.水库地震的综合概率增益预测法研究［J］.地震地质，31（4）：738－－746.

闫雪莲，周庆瑜，庞会敏，于冬梅.2009.水库诱发地震预测模型及定量预测［J］.东北水利水电，27（2）：43－－46.

张飞宇，王晓青，付虹，丁香，王龙，郑友华.2009.水库地震最大震级预测初步研究［J］.地震地质，31（4）：747－－757.

Baecher G B，Keeney R L.1982.Statistical examination of reservoir－induced seismicity［J］.Bull Seism Soc Amer，72（2）：553－－569.

Gupta H K.2002.A review of recent studies of triggered earthquakes by artificial water reservoirs with special emphasis on earthquakes in Koyna，India［J］.Earth－Science Reviews，58（3－－4）：279－－310.

A statistical study on the prediction of maximum magnitude of reservoir－induced earthquakes

10.3969/j.issn.0253－3782.2012.05.010

P315.1

A

国家科技支撑计划“水库地震预测方法研究”课题（2008BAC38B03）资助.

2011－10－25收到初稿，2012－02－21决定采用修改稿.

http：∥www.cnki.net/kcms/detail/11.2021.P.20120830.1420.006.html

王博，蒋海昆，宋金.2012.水库诱发地震震级预测的统计研究.地震学报，34（5）：689－－697.

Wang Bo，Jiang Haikun，Song Jin.2012.A statistical study on the prediction of maximum magnitude of reservoir－induced earthquakes.Acta Seismologica Sinica，34（5）：689－－697.