强震、微震记录数据差异的模型验算＊

崔庆谷华 均 杨 星

（中国昆明650224云南省地震局）

强震、微震记录数据差异的模型验算＊

（中国昆明650224云南省地震局）

在分析强震观测与微震观测本质区别的基础上，以已知的地震波强度资料为参照，通过对比FBS－3B型微震计及BBAS－2型强震加速度计的仪器噪声，揭示了仪器噪声、响应类型对两种仪器检测灵敏度的影响.我们对小湾台网记录到的一次微震进行了模拟计算.用正弦子波叠加合成地震记录作为地震计摆体响应方程的输入，通过计算，获得了微震计和强震加速度计的输出.对输入和输出数据进行分析，证明了两种仪器对远震长周期信号的监测能力存在显著差异，这种差异来源于强震计与微震计检测下限的不同.

强震计 微震计 数据仿真 数据差异

Abstract：With somekNown typical seismic data as reference，we analyzed the essential differences between strong motion observation and small earthquake observation，and compared the electric noises of FBS－3B seismometer and BBAS－2 accelerator.We carried out a synthetic simulation using the data of a small earthquake recorded by Xiaowan network.The result reveals the influence of electric noise and response type of the sensors on their sensitivities to ground motion.With asynchronous synthetic sine waves as input of a pendulum response equation，the output of a seismometer and accelerator is obtained.The sensitivities of the sensors to a tele－seismic wave prove to be quite different and it is this difference that leads to the distinction of recorded data.

Key words：strong motion accelerator；seismometer；simulation record；distinction of records

引言

地震引起的地面运动可以用位移、速度或加速度随时间的变化来表示.3种表示方式所使用的物理量不同，但本质上是同一运动的不同表现形式，因此，不同表示方式之间存在确定的量化关系，理论上可以互算.

与描述地面运动的3种方式相对应，用于记录真实地面运动的地震计可以是位移型、速度型或加速度型.目前国内的主流地震计是速度型和加速度型.其中速度型地震计主要用于微震观测，加速度型地震计主要用于强震观测.但国内外一些用于微震观测的宽频带地震计（如STS－1、STS－2和BBVS－120）同时具有加速度输出（DC—360 s或DC—120 s）和速度输出（360 s—50Hz或120 s—50Hz）.两种输出覆盖了目前科研所关注的地面运动信号的全部频段.与强震加速度计相比，尽管微震计的观测幅度范围不同，但都覆盖了50Hz以下的频段.

随着强震观测台网的扩大，有学者利用加速度记录数据仿真微震观测中的速度记录并得到了有价值的结果（金星等，2004a，b，c）.在此基础上，部分区域台网开始尝试利用强震记录进行大震速报以解决微震台网的大震限幅问题（张森等，2008）.

理论上，由于位移、速度、加速度3种表述方式之间存在确定的量化关系，因此在没有信号损失的前提下，同一测点上的强震记录与微震记录数据应该是可以互相转换的.在国内，由数字速度型记录仿真各种传统地震仪记录已经广泛应用于地震观测实践中.但是，大量的同点对比观测实验证明，当把速度记录与同点观测的加速度记录进行互算仿真时，许多情况下的仿真结果与实际记录在细节上不相吻合，有时甚至严重偏离.

长期以来，人们倾向于把这种偏离归因于算法的优劣，而不是怀疑产生这种现象的更深层原因.在工程应用中，以真实记录为蓝本的地震波合成甚至不考虑仿真结果与真实记录在细节上的一致，只追求两者统计特征的基本相同（李英民，赖明，1998），强震与微震记录数据难以精确互算的问题同样没有引起足够的重视.实质上，由于数据类型及检测下限的差异，强震数据与微震数据一般难以精确互算（特殊情况除外），由一种数据仿真另一种数据往往偏离实际观测结果.

作者分析了数据类型及检测下限不同引起的强震、微震记录数据差异及对地震监测能力的影响，并以人工合成地震动为输入，用模型验算方法证明检测下限不同是引起强震与微震记录数据难以精确互算的重要原因.

1 检测下限及数据类型差异对监测能力的影响

强震加速度计及微震计能够检测到的最小地面运动信号由各自的仪器自噪声水平决定.而仪器的自噪声水平可以用相关分析法测试得到.根据已有测试结果，云南台网目前使用的强震加速度计BBAS－2在1.0Hz处的RMS值（1/3倍频）约为5×10－6g（1g＝9.8 m/s2），FBS－3B在1.0Hz处的RMS值（1/3倍频）约为3.16×10－9m/s.由于上述两种地震计的仪器噪声不同、检测下限不同，同台观测能够检测到的最小地震事件也不同，只有振幅高于检测下限的地震事件能够被检测到并被记录下来.

由仪器噪声决定的检测下限可以看成是由多种频率的正弦子波叠加而成的.因此，BBAS－2及FBS－3B的检测下限转换为位移检测下限时满足：v0＝a0/ω，d0＝v0/ω＝a0/ω2.其中，v0，a0，d0，ω分别为速度下限、加速度下限、位移下限及合成地震动的正弦子波频率.根据上述转换关系，将BBAS－2和FBS－3B的仪器噪声振幅谱转换为位移振幅谱密度（A/T）时为两条随频率变化的曲线（图1）.

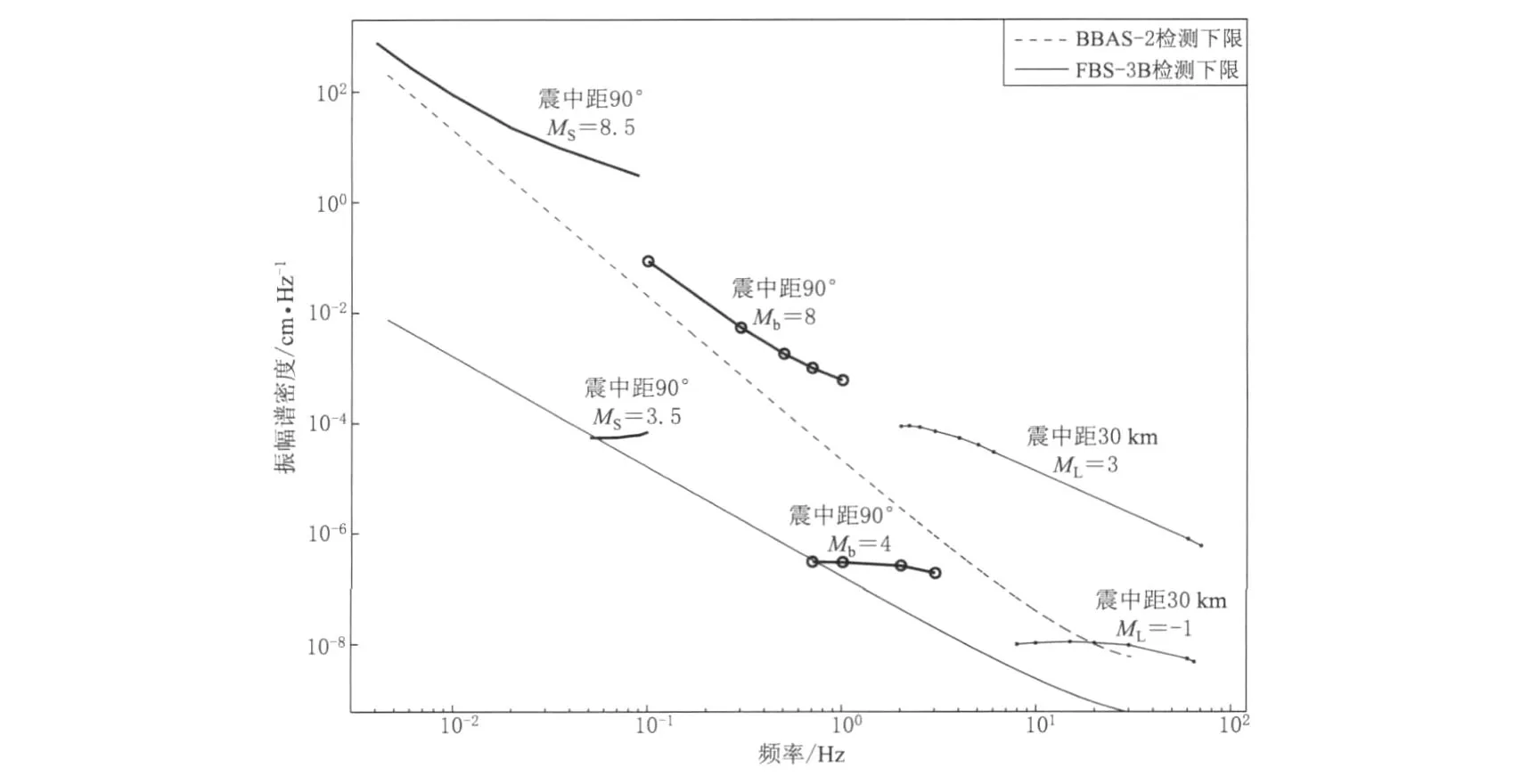
图1 FBS－3B微震计及BBAS－2强震加速度计对微震（Δ≈30km）及远震（Δ≈90°）监测能力的对比Fig.1 Difference in sensitivity of the seismometer FBS－3B and the accelerator BBAS－2 to a tele－seismic wave（Δ≈90°）and a near－field seismic wave（Δ≈30km）

如果地震事件的振幅已知，把这些振幅数据与上述两种地震计的检测下限数据相比较，就可以知道这些地震事件是否在地震计的检测范围之内，并可以用这些数据评判两种地震计的监测能力差异.

地震波的振幅和频率随震级、震中距而变化的规律十分复杂.前人对Δ≈30km处的微震S波以及Δ≈90°处的远震面波有过专门的研究，并得到了振幅随频率、震级变化的数据（Aki，Richards，1980；Bormann，2002）.将上述数据与BBAS－2和FBS－3B的检测下限绘制在同一个图形中，得到了两种地震计监测能力差异的对比图（图1）.

从图1中可以看出，FBS－3B型微震计可以监测到Δ＝30km处ML1—3的微小地方震，以及Δ＝90°处Mb4—8，MS3.5—8.5的远震.强震加速度计BBAS－2对Δ＝30km处微小地震的监测能力比微震计FBS－3B略低.对于ML＝1.0（甚至更大）的地震事件，其波形数据中低频成分的振幅小于BBAS－2的检测下限，只有高频部分的信号被检测到并被记录下来.

为进一步揭示两种地震计对远震及4.0级以下近震的监测能力的差异，以Mb＝4地震的P波振幅（优势频率1Hz）及MS＝4地震的面波振幅（优势周期20 s）随震中距的变化曲线为参照，可以得到两种地震计的监测能力对比图（图2）.

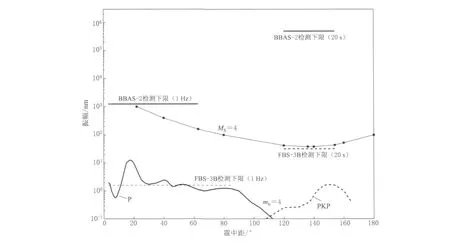
图2 FBS－3B微震计及BBAS－2强震加速度计对Mb＝4（优势频率1Hz）及MS＝4（优势周期20 s）地震监测能力的对比Fig.2 Difference in sensitivity of the seismometer FBS－3B and the accelerator BBAS－2 to a Mb＝4 seismic event（dominant frequency 1Hz）and a MS＝4 seismic event（dominant period 20 s）

从图2可以看出，微震计能够监测到约500km以内Mb4.0以上地震的P波（优势频率1Hz）及全球所有MS4.0以上的面波（优势频率20 s），但强震计的检测下限远大于P， PKP波的振幅，因而不能监测到上述震相.同样，对于长周期面波，微震计FBS－3B理论上能够监测到全球MS4.0以上地震的瑞利面波（LR，Airy震相周期T≈20 s）.但BBAS－2却无法检测到.可见，强震观测与微震观测在远震及Mb4.0，MS4.0以下近震监测中表现出显著的差异.

对于震中距500—1 000km（约5°—10°）范围内的近震，即使加速度计BBAS－2工作在高灵敏度档位也不能检测到Mb4.0地震的P波.P波信号的缺失说明强震加速度记录已经不完整，此时即使S波和面波能够被完整地记录到，记录数据也会由于P波信号的损失而失真.因此，震中距500km以上、Mb4.0、MS4.0以下近震不在强震监测的能力范围之内.

对于微小的地震事件，如果在使用加速度计时选择低灵敏度档位（如±2g，±4g等），微小信号成分将无法检测到，强震记录数据将存在信号损失，这一结论可以用模型验算的方法加以证实.

2 强震记录数据中信号损失的模型验算

2.1 基于正弦子波叠加的地震动合成

基于正弦子波叠加的地震动合成（Housner，1975；崔庆谷等，2011）必须考虑物理过程的可实现性，因为岩石受力并产生运动的过程伴随着变形的积累.力、变形都只能从零开始并逐渐增大，理想的阶跃在物理上是不可实现的.因此，在波形叠加过程中必须严格控制叠加相位，使叠加后的波形不产生阶跃，同时依靠相位差的分布来控制合成振幅的大小.

以小湾台网记录到的一次Δ＝23.9km，ML＝2.4微震的统计特征为模版，用正弦子波叠加合成的人工地震波为输入来验证强震、微震记录数据的差异.正弦子波的详细参数见表1.依据表1在参数叠加后得到的地震动加速度和速度见图3.

表1 合成地震动的正弦子波振幅、频率及到时表Table 1 Parameters of sine waves for constructing artificial seismic events

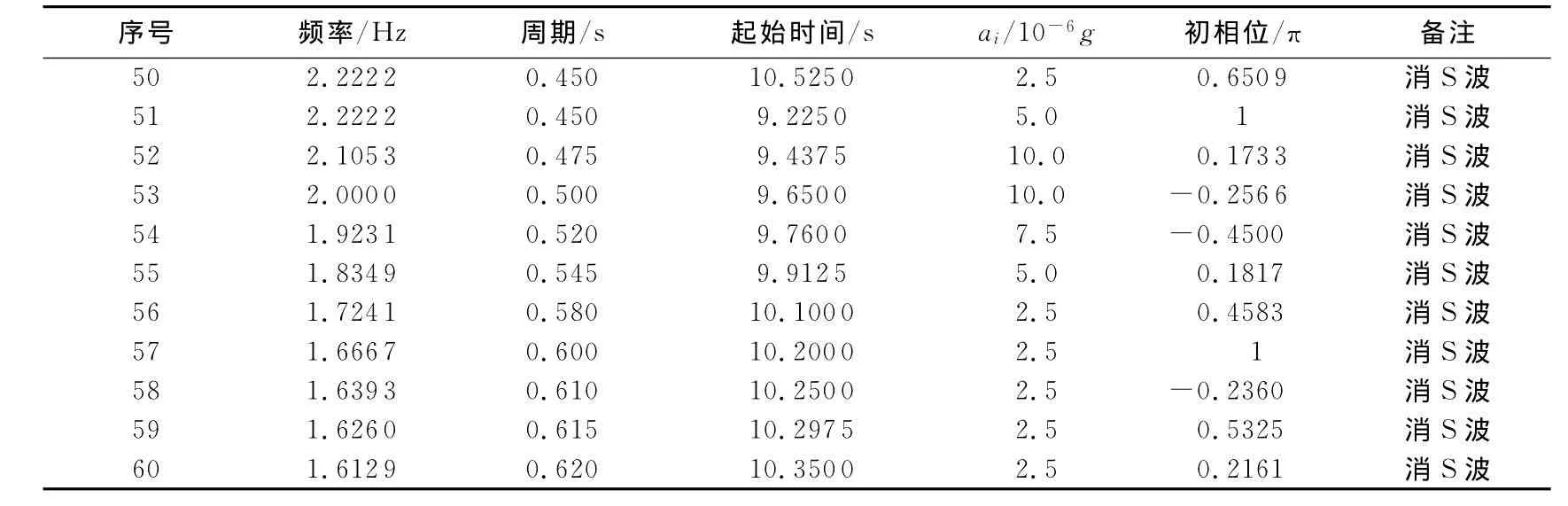
续表1

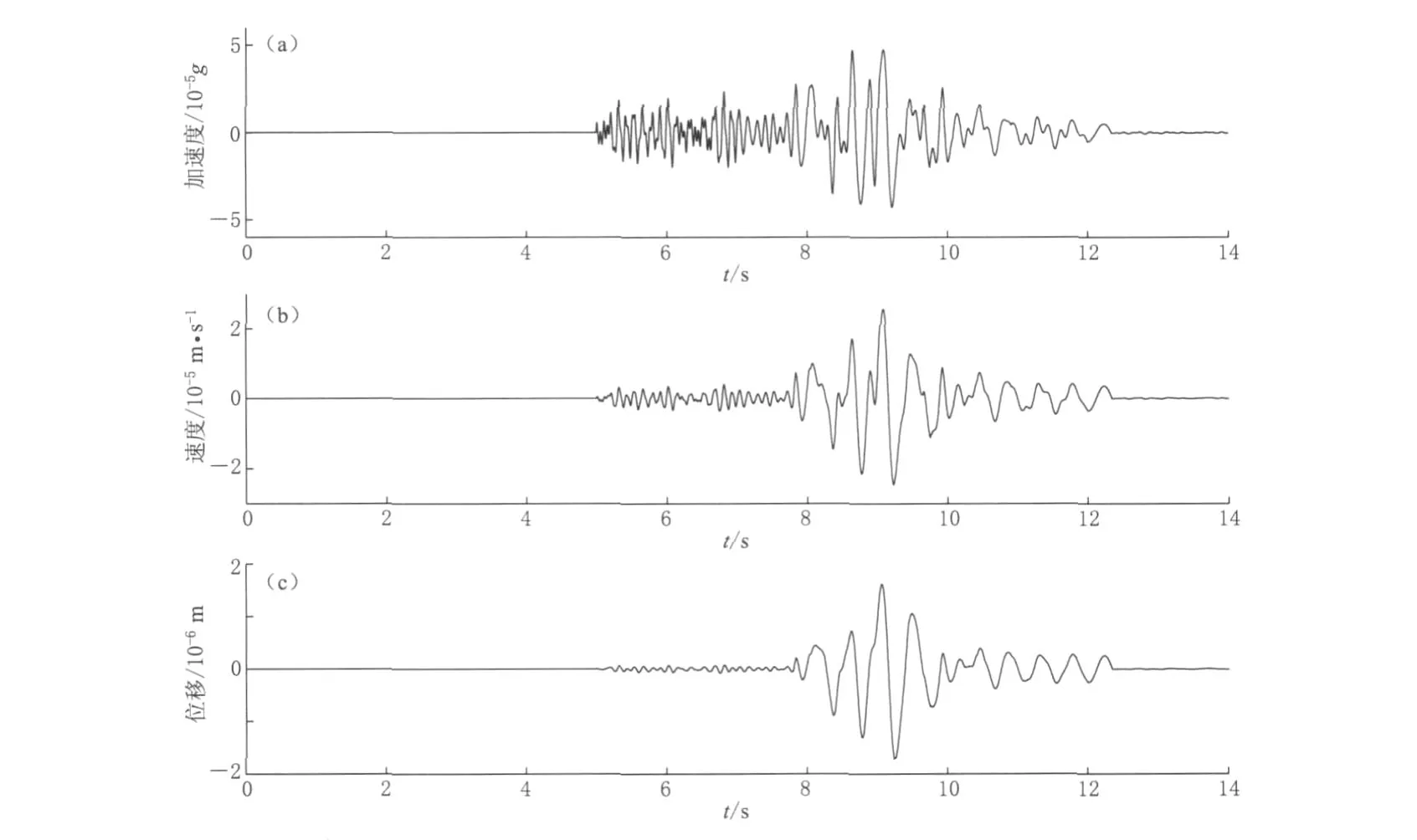
图3 合成地震动加速度时程（a）、速度时程（b）和位移时程（c）Fig.3 Time history of acceleration（a），velocity（b）and displacement（c）of an artificial seismic wave

2.2 地震计稳态响应计算

地震计摆体的响应方程为

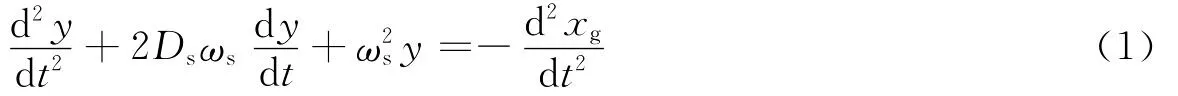
式中，y为摆体运动位移，xg为地面运动位移，Ds为摆体的阻尼系数，ωs为摆体的自振角频率.假设方程（1）的输入信号是一系列正弦子波叠加而成的地面运动加速度，即

上式对应的速度表达式为

式中，ai为与ωi对应的加速度振幅，ωi为信号角频率，vi＝ai/ωi为速度振幅.由于式（1）为常系数线性微分方程，体系对叠加信号的响应等于对单个正弦信号响应的叠加.假设摆体的初始位移为零，则加速度计摆体的稳态响应位移为（徐龙军等，2005；吴琛，周瑞忠，2007）

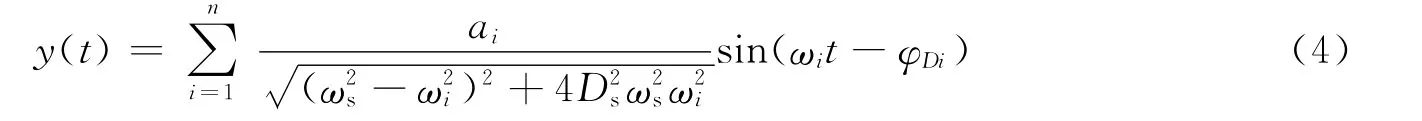
式中

对于磁动式速度地震计，摆体对上述信号的速度响应表达式为

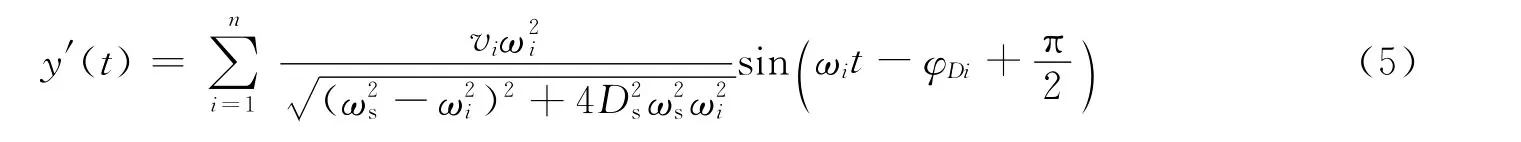
式中，y′（t）为摆锤的速度.

强震加速度计BBAS－2与微震速度型地震计FBS－3B同台记录，两种地震计的检测下限由仪器噪声的位移振幅谱密度曲线（图1）决定，计算过程如下.

由于地震计对叠加信号的响应等于对单个信号响应的叠加，因此，对于振幅大于检测上限的正弦信号，可以根据上述原理先分别求解地震计对单个信号的响应输出，然后再叠加得到地震计对合成地震波的输出.但是，对于振幅低于检测下限的多个正弦信号，不能因为其单一振幅低于检测下限而简单地采取舍去的办法来处理.本文的处理方法是：先将低于检测下限的子波信号进行叠加并得到叠加信号，再把叠加信号的振幅与仪器噪声的频域均方根值（2－decades带宽，约等于合成地震波频带）进行对比，振幅大于噪声均方根值的数据参与到理论输出波形的合成中，小于仪器噪声均方根值的数据归零处理.

BBAS－2自振周期T1＝0.01 s，阻尼比Ds1＝0.707；FBS－3B的自振周期T2＝20.0 s，阻尼比Ds2＝0.707.把上述参数代入式（4），（5），并参考BBAS－2的灵敏度数据（0.254 9 Vs2/m）及数据采集器的转换因子（3.814×10－9V/counts），可计算得到FBS－3B的理论记录波形（图4a），以及用BBAS－2数据仿真FBS－3B记录的波形（图4b）.

对比图4a与b可见，振幅较小的P波及尾波部分因小于检测下限而无法记录到，仿真数据的振幅较小，且波形与理论记录波形有较大误差.

设理论记录与仿真记录之间的绝对误差为ΔE（count）、相对误差为r.

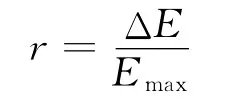
式中，Emax为理想输出记录的最大值（count）.通过统计计算，可以得到两种地震计模型验算结果的误差分布密度函数P（r）

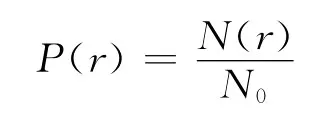
其中，N（r）为相对误差等于r的点的个数，N0为波形总的采样点数.最终得到仿真波形与理想记录波形的误差分布密度函数值（图4c）.

从图2中可以看出，尽管合成地震动的频率同时处于BBAS－2及FBS－3B两种地震计的检测通带范围内，但用BBAS－2记录数据仿真FBS－3B记录波形得到的结果与FBS－3B的理论输出发生了偏离.其原因在于：低于BBAS－2加速度计检测下限的输入信号不能被检测到，导致仿真结果出现误差.

3 讨论与结论

微震计及强震加速度计能够检测到的最小地面运动信号取决于两种仪器各自的仪器噪声水平.由于仪器噪声水平不同，它们能够检测到的最小地面运动信号的强度也不一样.对于强震加速度计，由于其仪器噪声强度普遍大于微震计，所以微震计能够检测到的部分微小信号在强震加速度记录中被仪器噪声所淹没而无法得到，因此强震记录与微震记录相比存在信号损失，两种数据在一般情况下难以精确互算。

强震观测与微震观测的区别在日常记录数据上表现为两者对长周期远震信号以及500km以内4.0级以下近震P波及面波信号的监测能力存在显著差异.对于以长周期振动为主的远震信号及脉动信号，加速度计的监测能力远远小于微震计，因而不可能从强震记录数据中提取微小地面运动信息.

对于震中距500km以内、Mb或MS小于4.0的近震，强震加速度计不能记录到完整的地震事件波形.

对于以高频成分为主的微小地方震，如果强震计的工作灵敏度较低，小震事件中振幅较小的信号成分无法被强震计检测到，这种信号损失将导致强震与微震数据无法精确互算.

崔庆谷，师娅芳，邓存华.2011.两种宽频带地震计高频段性能及记录数据差异的对比研究［J］.地震学报，33（3）：397－－403.

金星，马强，李山有.2004a.利用数字强震仪记录实时仿真地动速度［J］.地震工程与工程振动，24（1）：49－－54.

金星，马强，李山有.2004b.利用数字化速度记录实时仿真位移与加速度时程［J］.地震工程与工程振动，24（6）：9－－14.

金星，马强，李山有，杨文东.2004c.宽频带强震仪与地震仪同台基上的记录仿真对比研究［J］.地震工程与工程振动，24（5）：7－－12.

李英民，赖明.1998.工程地震动模型化研究综述及展望（1）［J］.重庆建筑大学学报，20（2）：192－－203.

吴琛，周瑞忠.2007.地震瞬态反应计算与结构位移反应谱研究［J］.水利发电学报，26（5）：53－－58.

徐龙军，谢礼立，郝敏.2005.简谐波地震动反应谱研究［J］.工程力学，22（5）：7－－13.

张森，杨周胜，颜其中，蔡绍平.2008.利用云南测震台网强震仪记录测定汶川主震震级［J］.地震研究，31（增刊）：480－－485.

Aki K，Richards P G（著）.1980.李钦祖，邹其嘉（译）.1986.定量地震学：理论和方法（第一卷）［M］.北京：地震出版社：552－－554.

Bormann P（著）.2002.中国地震局监测预报司（译）.2006.新地震观测实践手册（第一卷）［M］.北京：地震出版社：94－－100.

Housner G W.1975.Properties of strong motion earthquake［J］.Bull Seism Soc Amer，45（3）：197－－218.

Checking the distinction between accelerator and seismometer records by means of mathematical model

10.3969/j.issn.0253－3782.2012.05.008

P315.73

A

云南省自然科学基金面上项目“暂态对单自由度体系地震动力响应的影响研究”（2008CD220）资助.

2011－09－27收到初稿，2012－03－02决定采用修改稿.

http：∥www.cnki.net/kcms/detail/11.2021.P.20120830.1420.003.html

崔庆谷，华均，杨星.2012.强震、微震记录数据差异的模型验算.地震学报，34（5）：667－－675.

Cui Qinggu，Hua Jun，Yang Xing.2012.Checking the distinction between accelerator and seismometer records by means of mathematical model.Acta Seismologica Sinica，34（5）：667－－675.